一、希尔排序

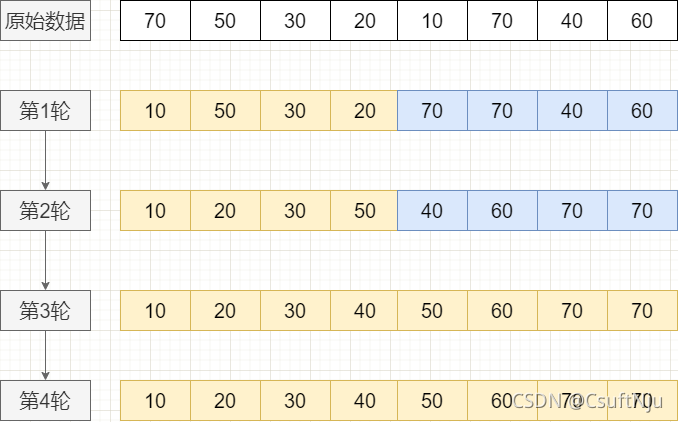
希尔排序又称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法，在对几乎已经排好序的数据操作时，效率极高，即可以达到线性排序的效率。

算法实现

1. 选择一个增量序列 T1，T2，……，Tk，其中 Ti > Tj, Tk = 1；

2. 按增量序列个数 z，对序列进行 z 趟排序；

3. 每趟排序，根据对应的增量 Ti，将待排序列分割成若干长度为 m 的子序列，分别对各子表进行直接插入排序。

4. 仅增量因子为 1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

复杂度

最好情况下的时间复杂度为O(n)，最坏情况为O(n^2)，空间复杂度为O(1)，是不稳定的算法

代码示例

void ShellSort(SqList *L)
{
    int i, j;
    int incr = L->length;
    do
    {
        incr = incr/3 + 1;
        for(i = incr; i <= L->length; i++)
        {
            if(L->r[i] < L->r[i - incr])
            {
                L->r[0] = L->r[i];
                for(j = i - incr; j > 0 && L->r[0] < L->r[j]; j -=incr)
                    L->r[j + incr] = L->r[j];
                L->r[j + incr] = L->r[0];
            }
        }
    }
    while(incr > 1);
}

另一种写法

void shellSort(int arr[], int n) {
    int i, j, gap;
    for (gap = n / 2; gap > 0; gap /= 2) {
        for (i = 0; i < gap; i++) {
            for (j = i + gap; j < n; j += gap) {
                for (int k = j; k > i && arr[k] < arr[k-gap]; k -= gap) {
                    swap(arr[k-gap], arr[k]);
                }
            }
        }
    }
}

图示过程

二、堆排序

堆是具有下列性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。这里需要注意从堆的定义可知，根结点一定是堆中所有结点最大(小)者。较大(小)的结点一般靠近根结点。 

堆排序( Heap Sort )就是利用堆(假设利用大顶堆)进行排序的方法。它的基本思想是，将待排序的序列构造成一个大顶堆。此时，整个序列的最大值就是堆顶的根结点。将它移走(其实就是将其与堆数组的末尾元素交换，此时末尾元素就是最大值),然后将剩余的n-1个序列重新构造成一个堆， 这样就会得到n个元素中的次小值。如此反复执行，便能得到一个有序序列了。

 算法实现

首先把待排序的元素按照大小在二叉树位置上排列，且要满足堆的特性，如果根节点存放的是最大的数，则叫做大根堆，反之就叫做小根堆了。

根据这个特性就可以把根节点拿出来，然后再用父节点和他的孩子节点进行比较，取最大的孩子节点和其进行交换，再把根节点拿出来，一直循环到最后一个节点，就排序好了。

复杂度

时间复杂度为O(nlogn)，空间复杂度为O(1)，是不稳定排序

代码示例

void HeapAdjust(vector<int>& nums, int left, int right)
{
    int temp = nums[left];
    for (int j = (left + left + 1); j <= right; j += (j + 1))
    {
        if (j < right && nums[j] < nums[j + 1]) ++j;
        if (temp >= nums[j]) break;
        nums[left] = nums[j];
        left = j;
    }
    nums[left] = temp;
}

void HeapSort(vector<int>& nums)
{
    int i, n = nums.size();
    for (i = n >> 1; i >= 0; --i)
        HeapAdjust(nums, i, n - 1); for (int& i : nums)cout << i << ' '; cout << endl;
    for (i = n - 1; i > 0; --i)
    {
        swap(nums[0], nums[i]);
        HeapAdjust(nums, 0, i - 1); for (int& j : nums)cout << j << ' '; cout << i << endl;
    }
}

int main() {
    vector<int>vec = { 5,2,1,7,3,9,8,4,6 };
    int n = vec.size();
    HeapSort(vec);
    return 0;
}

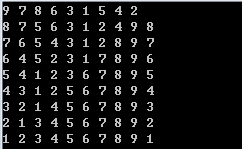
输出结果如下：

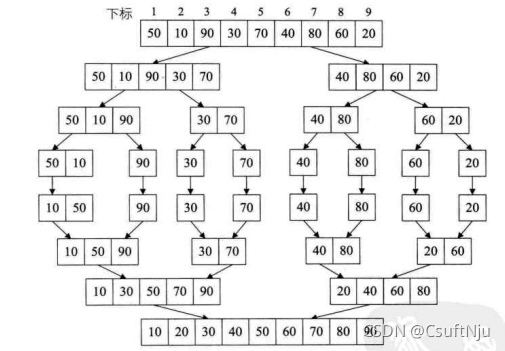
三、归并排序

 归并排序(Merging Sort)就是利用归并的思想实现的排序方法。原理是假设初始序列含有n个数，则可以看成是n个有序的子序列，每个子序列的长度为1，然后两两归并，得到[n/2] (不小于n/2的最小整数)个长度为2或1的有序子序列，再两两归并，如此重复，直至得到一个长度为n的有序序列为止，这种排序方法称为2路归并排序。

 算法实现

将已有序的子序列合并，得到完全有序的序列，即先使每个子序列有序，再使子序列段间有序。过程如下：

1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列

2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置

3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置

4. 重复上一步骤直到某一指针超出序列尾

5. 将另一序列剩下的所有元素直接复制到合并序列尾

 复杂度

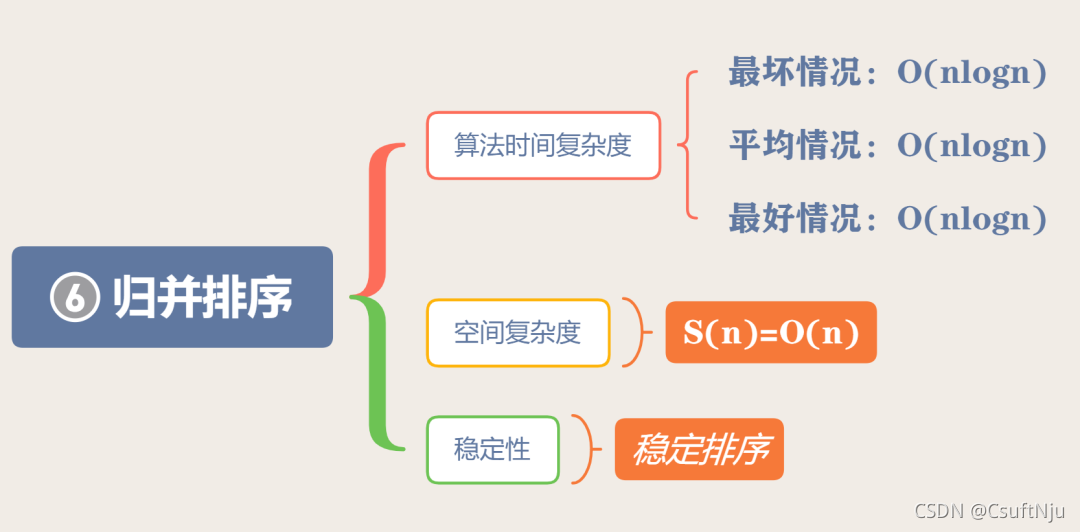
代码示例

void merge(vector<int>& arr, int l, int mid, int r) {
    vector<int>aux(r - l + 1, 0);//开辟新数组，将原数组映射进去
    for (int m = l; m <= r; m++) {
        aux[m - l] = arr[m];
    }
    int i = l, j = mid + 1;//i和j分别指向两个子数组开头,k指向原数组待排序位置
    for (int k = l; k <= r; k++) {
        if (i > mid) {
            arr[k] = aux[j - l];
            j++;
        }
        else if (j > r) {
            arr[k] = aux[i - l];
            i++;
        }
        else if (aux[i - l] < aux[j - l]) {
            arr[k] = aux[i - l];
            i++;
        }
        else {
            arr[k] = aux[j - l];
            j++;
        }
    }
}

void merge_sort(vector<int>& arr) {
    int n = arr.size();
    for (int sz = 1; sz < n; sz += sz) {    //子序列长度从1到小于n的(2的次方)(比如长度为9,子序列最长为8)
        cout << "substring long : " << sz << " result : ";
        for (int i = 0; i + sz < n; i += sz + sz) { /*比如子序列长度为2，此时序列为2 5,1 7|3 9,4 8，6.
先对2 5,1 7排序,再对3 9,4 8排序.所以i+(2+2),下标位置从2变为3.同时确保i+sz(4)不越界.*/
           
            merge(arr, i, i + sz - 1, min(i + sz + sz - 1, n - 1));//min函数防止越界,应对在数组末尾，第二个子序列长度小于第一个的情况。
            for (int i : arr)cout << i << ' ';
            cout << "next ";
        }
        cout << endl;
    }
}
int main(int argc, const char* argv[]) {
    vector<int>vec = { 2,5,1,7,3,9,8,4,6 };
    merge_sort(vec);
    return 0;
}

 图示过程

查看上面的程序输出，如下所示，依次对相邻两个子序列排序，子序列长度从1到8.每次排序的两个子序列为红框内的数。