图神经
GraphSAGE (Inductive Representation Learning on Large Graphs, NIPS2017)
GraphSAGE是一种能够利用节点的属性信息高效产生未知节点嵌入的一种归纳式学习(Inductive Learning)的框架,其核心思想是通过学习一个对邻域节点进行聚合表示的函数来生成目标节点的嵌入。
1. Embedding generation
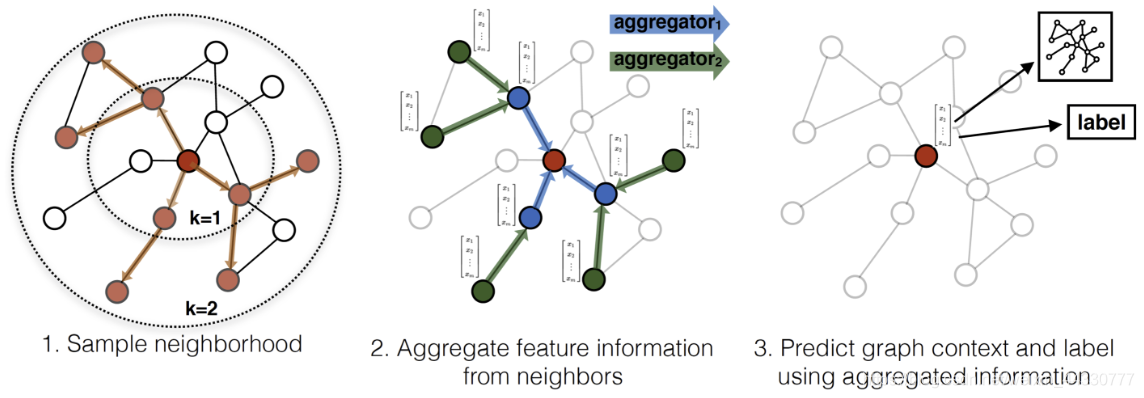
GraphSAGE = Graph SAmple and aggreGatE,即图的采样和聚合,具体过程如下图所示:
对节点的邻居进行采样
聚合所采样邻居的特征信息
根据聚合的信息生成嵌入,预测图内容或标签
 将该过程表述成算法如下:
将该过程表述成算法如下:
外层循环的K代表着网络层数,也就是中心节点所能聚合到的邻居阶数,同时也代表着聚合次数,也是聚合函数个数。
文中通过实验测试出:当 K=2 时(中心节点最多可以将其二阶邻域的节点信息聚合到自己的嵌入表示中),当一阶邻域数与二阶邻域数的乘积 S 1 ∗ S 2 < 500 S1*S2<500S1∗S2<500时,模型就可以达到很好的效果。
在内层循环中,对每个节点 v ,首先使用 v的邻居节点的 k-1 层的嵌入表示 h u k − 1 h_u^{k-1}huk−1 来通过聚合函数生成 v的邻居节点的 k层表示h N ( v ) h_{N(v)}hN(v) 。之后将 h N ( v ) h_{N(v)}hN(v)和节点 v的第 k-1 层的嵌入表示 h v k − 1 h_v^{k-1}hvk−1 进行拼接,经过一个非线性变换 W k W^kWk产生节点 v的第 k层的嵌入表示 h v k h_v^khvk。
2. Aggregator Architectures
由于在图中节点的邻居是天然无序的,所以希望构造出的聚合函数是对称的(inherently symmetric),即改变输入的顺序,函数的输出结果不变。
Mean aggregator
Mean aggregator类似于GCN框架中使用的卷积传播规则。将嵌入生成算法的4、5行替换为下式来得出该方法的归纳变量,直接产生目标节点的向量表示,而不是邻居节点的向量表示。Mean aggregator将目标节点和邻居节点的第 k-1 层嵌入拼接起来,然后对其每个维度进行求均值,再将得到的结果做一次非线性变换 W,生成目标节点的第 k层嵌入表示。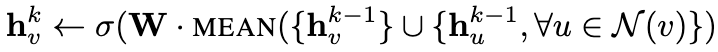
LSTM aggregator
引入循环神经网络LSTM来encode邻居的特征,有更强的表示能力。由于LSTM不是对称(inherently symmetric)的,所以在使用时需要对目标节点的邻居进行随机打乱,再输入到LSTM中。
Pooling aggregator
先对目标节点的每个邻居节点的嵌入表示独立进行非线性变换(MLP) W p o o l W_{pool}Wpool得到向量,之后把所有邻居节点的向量做一次池化操作(max pooling / mean pooling)进行聚合,该工作中采用了max pooling。
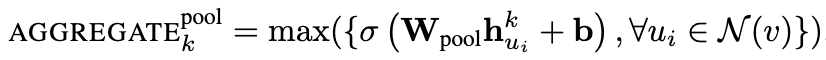
3. Learning the parameters
以上是GraphSAGE的前向传播过程,下面简单介绍训练过程。
为了在完全无监督的情况下学习有用的预测表示,该工作基于图的输出表示z u z_uzu的损失函数进行参数学习——权重矩阵 W k W_kWk和聚合函数的参数。 基于图的损失函数,希望相近的节点具有相似的表示,分离节点有不同的表示: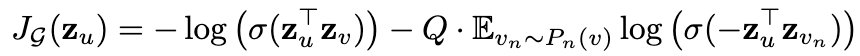
其中 v是在定长随机游走中出现在 u附近的节点,σ \sigmaσ是sigmoid函数, P n P_nPn是负采样分布, Q是负样本数量。
不同于以前的嵌入方法,z u z_uzu是由一个节点的局部邻域所包含的特征生成的,而不是为每个节点训练唯一的嵌入。
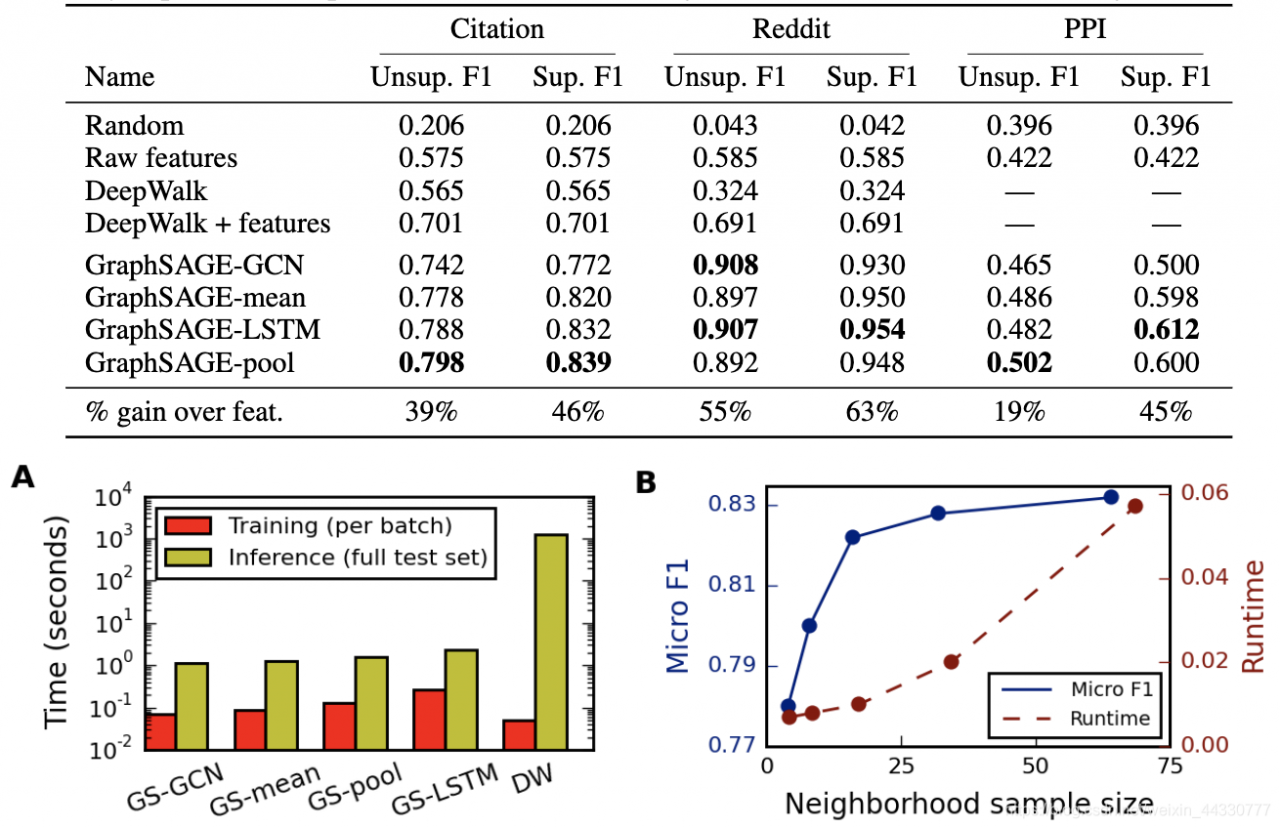
4. 实验
最终的实验结果表明,在GraphSAGE中LSTM和pooling聚合的方法效果最好。
5. 思考
GraphSAGE有必要和GCN相比较进行思考:
本质上来说,GCN(归一化邻接矩阵后乘以特征矩阵)也是一种均值聚合的过程。而两者的区别在于,GCN中的邻接矩阵是固定的,并且只支持整张图一起训练,这就导致了它对于新节点/新边的动态适应力不足。
本质上来说,GraphSAGE的归纳式学习在于聚合函数中包含了对于邻居节点的聚合,即多了采样的过程,该过程中邻接矩阵是不断变化的,相当于从GCN中的固定参数变成了输入变量。
训练过程中的minibatch方法同理,每次提取的子图中同一个节点的邻接矩阵也很可能不同。
所以,相比于GCN,GraphSAGE的改进在于可以灵活地动态进行分批训练和采样。
GAT (Graph Attention Networks, ICLR2018)
该工作提出了图注意力网络(GAT)——在图结构化数据上运行的新型神经网络体系结构,利用masked self-attention层来解决基于图卷积或其类似的方法的缺点。 通过堆叠节点能够参与其邻域特征的层,为邻域中的不同节点指定了不同的权重,而无需进行任何昂贵的矩阵运算(如求逆)或依赖于已知的图。通过这种方式,可以同时解决基于频谱的图神经网络的几个关键挑战,并使该模型在归纳学习(inductive learning)上和传导学习(transductive learning)上一样易用。
1. 概念
传导学习(Transductive Learning):即前文提到的直推式学习,先观察特定的训练样本,然后对特定的测试样本做出预测。训练阶段与测试阶段都基于同样的图结构。
归纳学习(Inductive Learning):先从训练样本中学习到一定的模式,然后利用其对测试样本进行预测。训练阶段与测试阶段需要处理的图不同,通常是训练阶段只是在子图(subgraph)上进行,测试阶段需要处理未知的节点。
全局图注意力(global graph attention):顾名思义,就是每一个节点都对于图上任意顶点都进行attention运算。这样的优点是完全不依赖于图的结构,对于inductive任务无压力;缺点是丢掉了图结构的特征、运算面临着高昂的成本。
局部图注意力(masked graph attention):注意力机制的运算只在一阶邻居节点上进行,该工作中采用了这种方式。
2. 计算图注意力系数(attention coefficient)
graph attention layer
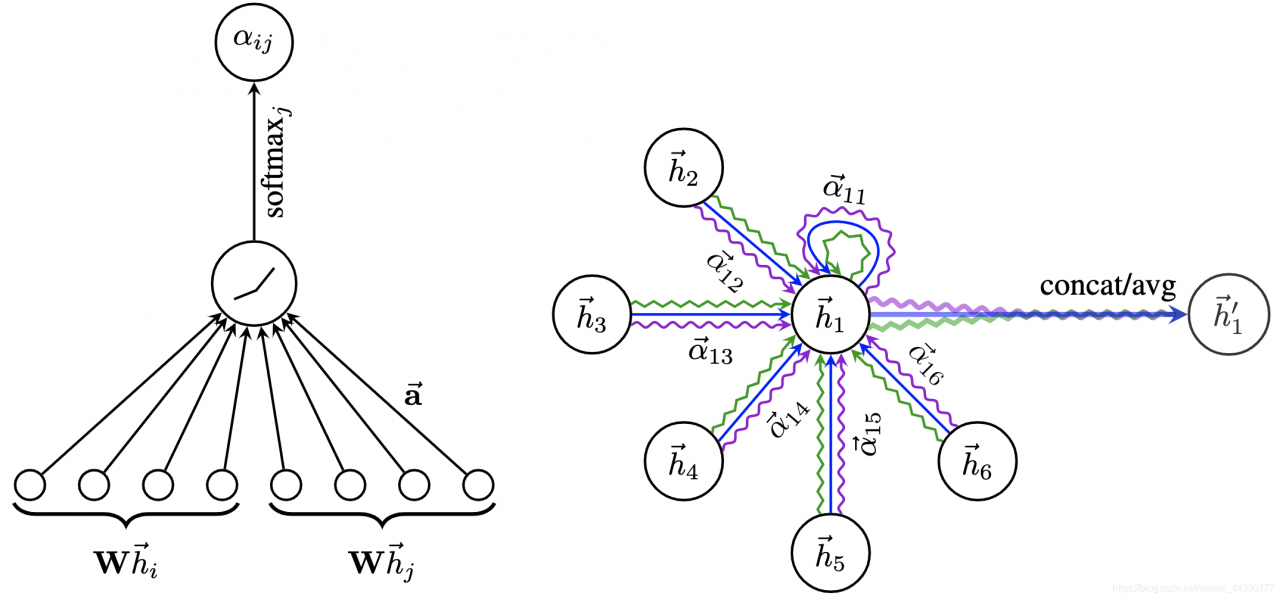
对于节点 i ii,逐个计算它的邻居们和它自己之间的相似系数:
e i j = a ( [ W h i ∥ W h j ] ) , j ∈ N i e_{ij}=a([Wh_i{\parallel}Wh_j]),j{\in}N_ieij=a([Whi∥Whj]),j∈Ni
其中,首先一个共享参数 W WW的线性映射对于节点的特征进行了增维,这是一种常见的特征增强(feature augment)方法;[ ⋅ ∥ ⋅ ] [\cdot{\parallel}\cdot][⋅∥⋅] 对于节点i , j i,ji,j的变换后的特征进行了拼接(concatenate);最后a ( ⋅ ) a(\cdot)a(⋅)把拼接后的高维特征映射到一个实数上,作者是通过 single-layer feedforward neural network实现的。
接下来基于相关系数进行归一化:
α i j = exp ( L e a k y R e L U ( e i j ) ) ∑ k ∈ N i exp ( L e a k y R e L U ( e i j ) ) \alpha_{ij}=\frac{\exp(LeakyReLU(e_{ij}))}{\sum_{k{\in}N_i}\exp(LeakyReLU(e_{ij}))}αij=∑k∈Niexp(LeakyReLU(eij))exp(LeakyReLU(eij))至此注意力系数α i j \alpha_{ij}αij求解完毕,过程如下图(左)所示:
3. 聚合(aggregate)
如同GraphSAGE一样,基于空间的图卷积网络绕不开聚合。在这里,聚合就是根据计算好的注意力系数 α i j \alpha_{ij}αij,把特征h j h_jhj加权求和:
h i ′ = σ ( ∑ j ∈ N i α i j W h j ) h_i'=\sigma(\sum_{\mathclap{j{\in}N_i}}\alpha_{ij}Wh_j)hi′=σ(∑j∈NiαijWhj)其中,h i ′ h_i'hi′就是GAT输出的对于每个节点 i ii的新特征(融合了邻域信息), σ ( ⋅ ) \sigma(\cdot)σ(⋅)是激活函数。
为了提高模型的拟合能力,在本文中还引入了multi-head attention,即同时使用多个W k W^kWk计算注意力,然后将各个 W k W^kWk计算得到的结果合并(连接):
h i ′ ( K ) = ∥ k = 1 K σ ( ∑ j ∈ N i α i j k W k h j ) h_i'(K)={\parallel}_{k=1}^{K}\sigma(\sum_{\mathclap{j{\in}N_i}}\alpha_{ij}^kW^kh_j)hi′(K)=∥k=1Kσ(j∈Ni∑αijkWkhj)其中,
∥ \parallel∥表示连接,α i j k \alpha_{ij}^kαijk和 W k W^kWk表示第 k个multi-head得到的计算结果。类似的,也可以用求和的方式进行合并:
h i ′ ( K ) = σ ( 1 K ∑ k = 1 K ∑ j ∈ N i α i j k W k h j ) h_i'(K)=\sigma(\frac{1}{K}\sum_{k=1}^{K}\sum_{\mathclap{j{\in}N_i}}\alpha_{ij}^kW^kh_j)hi′(K)=σ(K1k=1∑Kj∈Ni∑αijkWkhj) 聚合过程如上图(右)所示。
3. 理解
GCN与GAT都是将邻居顶点的特征聚合到中心节点上(一种aggregate运算),利用graph上的local stationary学习新的节点特征表达。不同的是GCN利用了拉普拉斯矩阵,GAT利用attention系数。GAT会更强,因为节点特征之间的相关性被更好地融入到模型中。
GAT的运算方式是逐节点的运算(node-wise),每一次运算都需要循环遍历图上的所有顶点来完成。逐节点运算意味着,摆脱了拉普利矩阵的束缚,使得有向图问题迎刃而解。
为什么GAT适用于归纳学习?GAT中重要的学习参数是 W与a ( ⋅ ) a(\cdot)a(⋅),因为上述的逐节点运算方式,这两个参数仅与节点特征相关,与图的结构毫无关系。所以测试任务中改变图的结构,对于GAT影响并不大,只需要改变邻居 N i N_iNi ,重新计算即可。与此相反的是,GCN是一种全图的计算方式,一次计算就更新全图的节点特征。学习的参数很大程度与图结构相关,这使得GCN在inductive任务上遇到困境。
一句话概括:GAT就是将注意力机制attention应用在了基于空间的图卷积网络上。