遗传算法设计实例

1.遗传算法实例程序设计

随机初始化种群P(t)={x1,x2…xn),计算P(t)中个体的适应值。其MATLAB程序的基本格式如下:

Begin
t=0
初始化P(t)
计算P(t)的适应值;
while (不满足停止准则)
	do
	begin
	t=t+1
	从P(t+1)中选择P(t)
	重组P(t)
	计算P(t)的适应值
end

例1 求函数 f(x) =9*sin(5x) + cos(4x)，x∈[0,15]的最大值

解：

初始化（编码）

%初始化
function pop = initpop( popsize, chromlength)
pop = round(rand(popsize, chromlength));
%rand随机产生每个单元为{0,1}行数为popsize,列数为chromlength的矩阵,
%roud对矩阵的每个单元进行圆整，这样产生的初始种群，
end
%round函数用于舍入到最接近的整数。语法形式只有1种：Y = round(X)，这里的X可以是数，向量，矩阵，输出对应。

initpop.m函数的功能是实现群体的初始化,popsize表示群体的大小,chromlength表示染色体的长度(二值数的长度),长度大小取决于变量的二进制编码的长度。

目标函数值

二进制数转化为十进制数

function pop2 = decodebinary(pop)
[px,py]= size(pop);
%求pop行和列数
for i= 1:py
    pop1(:,i)=2.^(py - i). * pop(:,i);
end
pop2 = sum(pop1,2);
%求popl的每行之和
end

二进制编码转化为十进制数

decodechrom.m函数的功能是将染色体(或二进制编码)转换为十进制,参数spoint表示待解码的二进制串的起始位置。对于多个变量而言,如有两个变量,采用20表示,每个变量为10,则第一个变量从1开始,另一个变量从11开始。

%将二进制编码转换成十进制
function pop2 = decodechrom( pop, spoint, length)
pop1 = pop(:, spoint:spoint + length- 1);
pop2 = decodebinary(pop1);
end

计算目标函数值

function  [abjvalue] = calobjvalue(pop)
templ = decodechrom(pop, 1,10); %将pop每行转化成十进制数
x= templ * 10/1023;             %将二值城中的数转化为变量域的数
abjvalue = 10* sin(5*x)+7* cos(4*x);%计算目标函数值
end

计算个体的适应值

%计算个体的适应值
function fitvalue = calfitvalue( objvalue)
global Cmin;
Cmin= 0;
[px, py]= size(objvalue);
for i = 1:px
    if objvalue(i) + Cmin>0
        temp = Cmin + objvalue(i);
    else
        temp = 0.0;
    fitvalue(i) = temp;
end
fitvalue = fitvalue'

选择复制

选择或复制操作是决定哪些个体可以进入下一代。程序中采用赌轮盘选择法选择，这种方法较易实现。根据方程 p_i= f_i/f_sum.选择步骤如下:
(1) 在第t代,计算f_sum和p_i。
(2)产生{0,1}的随机数rand(.),求s=rand(.)* f_sum。
(3)求 Σf_i ≥s中最小的k,则第k个个体被选中。
(4) 进行N次(2)、(3)操作,得到N个个体,成为第t=t+1代种群。

%选择复制
function [newpopl = selection(pop, fitvalue)
totalfit = sum(fitvalue);       %求适应值之和
fitvalue = fitvalue/ totalfit;  %单个个体被选择的概率
fitvalue = cumsum(fitvalue);    %如fitvalue=[1 2 3 4],则cumsum(fitvalue)=[1 3 6 10]
[px,py]= size(pop);
ms = sort( rand(px,1));         %从小到大排列
fitine 1;
newin= 1;
while newin <= px
    if(ms( newin))< fitvalue(fitin)
        newpop(newin) = pop(fitin);
        newin= newin+ 1;
    else
        fitin = fitin+1;
    end
end

交叉

群体中的每个个体之间都以一定的概率pc交叉，即两个个体从各自字符串的某一位置(一般是随机确定)开始互相交换,这类似生物进化过程中的基因分裂与重组。

例如,假设两个父代个体x1.x2为:
x1 =0100110
x2 = 1010001.
从每个个体的第3位开始交叉,交叉后得到两个新的子代个体y1、y2分别为:
y1 = 0100001
y2= 1010110
这样两个子代个体就分别具有了两个父代个体的某些特征。
利用交叉有可能由父代个体在子代组合成具有更高适合度的个体。事实上交叉是遗传算法区别于其他传统优化方法的主要特点之一。

%交叉
function [newpop] = crossover(pop, pc)
[px, py] = size(pop);
newpop = ones(size(pop));
for i= 1:2:px- 1  %2为间隔
    if(rand <pc)
        cpoint = round(rand* py);
        newpop(i,:) = [pop(i,1:cpoint),pop(i+ 1,cpoint+1:py)];
        nevpop(i+1,:)= [pop(i + 1,1:cpoint),pop(i,cpoint+ 1:py)];
    else
        newpop(i,:) = pop(i);
        newpop(i+ 1,:)=pop(i+1);
    end
end

变异
基因的突变普遍存在于生物的进化过程中。变异是指父代中的每个个体的每一位都以概率pm翻转,即由1变为0,或由0变为1。

遗传算法的变异特性可以使求解过程随机地搜索到解可能存在的整个空间,因此可以在一定程度上求得全局最优解。

%变异
function [newpop] = mutation( pop,pa)
[px,py]= size(pop); 
newpop = ones(size(pop);
for i= 1:px
    if(rand< pm)
        mpoint = round(rand * py);
    if mpoint<= 0
        mpoint= 1;
    end
        newpop(i) = pop(1);
            if any( newpop( i, mpoint))==0
                newpop( i, mpoint) = 1;
            else
                newpop(i, mpoint) = 0;
            end
    else
        newpop(i) = pop(i);
    end
end

求出群体中最大适应值及其个体

%求出群体中适应值最大的值
function [ bestindividual, bestfit] = best(pop, fitvalue)
[px,py]= size(pop);
bestindividual = pop(1,:);
bestfit= fitvalue(1);
for i= 2:px
    if fitvalue( i> bestfit
        bestindividual= pop(i,:);
        bestfit= fitvalue(i);
    end
end

主程序

clc;
clear all;
popsize= 20;        %群体大小
chromlength= 10;    %字符串长度(个体长度)
pc = 0.7;           %交叉概率
pm= 0.005;          %变异概率
pop = initpop(popsize, chromlength);    %随机产生初始群体
for i= 1:20         %20为迭代次数
    [objvalue] = calobjvalue(pop);         %计算目标函数
    fitvalue = calfitvalue(objvalue);      %计算群体中每个个体的适应度
    [newpop] = selection( pop, fitvalue);   %复制
    [newpop]  = crossover(pop, pc);         %交叉
    [newpop] = mutation(pop, pc);           %变异
    [bestindividual, bestfit]= best(pop, fitvalue); %求出群体中适应值最大的个体及其适应值
    y(i) = max(bestfit);
    n(i)= 1;
    pop5 = bestindividual;
    x(i) = decodechrom( pop5, 1, chromlength) * 10/1023;
    pop= newpop;
end
fplot(@(x)9.*sin(5.*x)+8.*cos(4.*x))
hold on
plot(x,y,'r* ')
hold off

结果如下：最高点为最大值

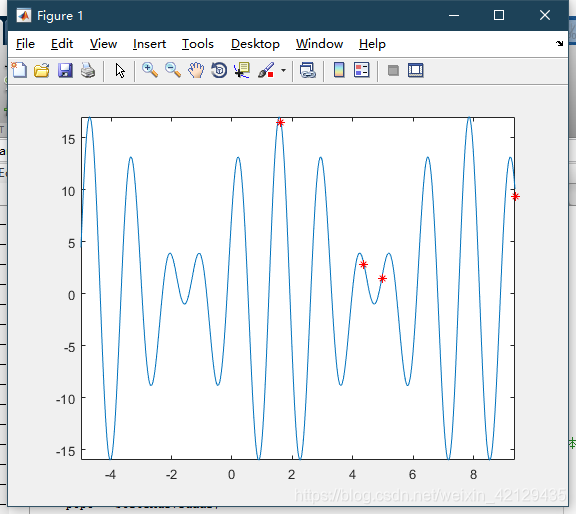
在这里插入图片描述
注意:遗传算法有4个参数需要提前设定,一般在以下范围内进行设置。

群体大小: 20~100。
遗传算法的终止进化代数: 100~500。
交叉概率: 0.4~0.99。
变异概率: 0. 0001~0.1。

注意

1算法的参数设计

在单纯的遗传算法中,有时候也会出现不收敛的情况,即使在单峰或单调也是如此。这是因为种群的进化能力已经基本丧失,种群早熟。为了避免种群的早熟,参数的设计一般遵从以下原则。

种群的规模

当群体规模太小时,很明显会出现近亲交配,产生病态基因。而且造成有效等位基因先天缺乏,即使采用较大概率的变异算子,生成具有竞争力高阶模式的可能性仍很小，.况且大概率变异算子对已有模式的破坏作用极大。

同时遗传算子存在随机误差(模式采样误差)，妨碍小群体中有效模式的正确传播，使得种群进化不能按照模式定理产生所预测的期望数量;种群规模太大,结果难以收敛且浪费资源,稳健性下降。种群规模的一个建议值为0~ 100。

变异概率

当变异概率太小时,种群的多样性下降太快，容易导致有效基因的迅速丢失且不容易修补;当变异概率太大时,尽管种群的多样性可以得到保证,但是高阶模式被破坏的概率也随之增大。变异概率一般取0. 0001~0.2。

交配概率

交配是生成新种群最重要的手段。与变异概率类似,交配概率太大容易破坏已有的有利模式,随机性增大,容易错失最优个体;交配概率太小不能有效更新种群。交配概率一般取0.4~0. 99.

进化代数

进化代数太小,算法不容易收敛,种群还没有成熟;代数太大,算法已经熟练或者种群过于早熟不可能再收敛,继续进化没有意义,只会增加时间开支和资源浪费。进化代数一般取100~500。

种群初始化

初始种群的生成是随机的。在初始种群的赋予之前，尽量进行一个大概的区间估计,以免初始种群分布在远离全局最优解的编码空间，导致遗传算法的搜索范围受到限制，同时也为算法减轻负担。

2.适应度函数的调整

在遺传算法运行的初期阶段

群体中可能会有少数几个个体的适应度相对其他个体来说非常高。若按照常用的比例选择算子来确定个体的遗传数量时,则这几个相对较好的个体将在下一代群体中占有很高的比例。

在极端情况下或当群体现模较小时,新的群体甚至完全由这样的少数几个个体所组成。这时交配运算就起不了什么作用,因为相同的两个个体不论在何处发生交叉行为都永远不会产生新的个体。

这样就会使群体的多样性降低,容易导致遗传算法发生早熟现象(或称早期收敛)，使遗传算法所求到的解停留在某一局部最优点上。

因此，希望在遗传算法运行的初期阶段,算法能够对–些适应度较高的个体进行控制,降低其适应度与其他个体适应度之间的差异程度,从而限制其复制数量,以维护群体的多样性。

在遗传算法运行的后期阶段

群体中所有个体的平均适应度可能会接近于群体中最佳个体的适应度。也就是说，大部分个体的适应度和最佳个体的适应度差异不大,它们之间无竞争力,都会有以相接近的概率被遗传到下一代的可能性,从而使得进化过程无竞争性可言,只是一种随机的选择过程。这将导致无法对某些重点区域进行重点搜索，从而影响遗传算法的运行效率。

因此,希望在遗传算法运行的后期阶段,算法能够对个体的适应度进行适当的放大，扩大最佳个体适应度与其他个体适应度之间的差异程度,以提高个体之间的竞争性。

原文链接：https://blog.csdn.net/weixin_42129435/article/details/118159968