蒙特卡罗求积分
@author--HCF
背景概述
为了解决某问题,首先需要把它变成一个概率模型的求解问题,然后产生符合模型的大量随机数,最后对产生的随机数进行分析从而求解问题,这种方法叫做Monte Carlo(蒙特卡罗)方法。
比如为了计算圆周率π \piπ的近似值可以使用随机模拟的方法。如果正方形D = { ( x , y ) : x ∈ [ − 1 , 1 ] , y ∈ [ − 1 , 1 ] } D=\{(x,y):x\in [-1,1],y\in[-1,1]\}D={(x,y):x∈[−1,1],y∈[−1,1]}内随机等可能投点,落入单位圆C = { ( x , y ) : x 2 + y 2 ≤ 1 } C=\{(x,y):x^2+y^2\le 1\}C={(x,y):x2+y2≤1}的概率为面积之比p = π 4 p=\frac{\pi}{4}p=4π。如果独立重复地投了N NN个点,落入C CC中的点的个数ξ \xiξ的平均值为E ξ = p N E\xi=pNEξ=pN,由概率的频率解释可以得到ξ N ≈ π 4 , π ≈ π ^ = 4 ξ N \frac{\xi}{N}\approx\frac{\pi}{4},~\pi\approx\hat{\pi}=\frac{4\xi}{N}Nξ≈4π, π≈π^=N4ξ,从而可以求出π \piπ。
上例中估计的π ^ \hat{\pi}π^实际上是随机的,如果再次独立重复投N NN个点,得到的π ^ \hat{\pi}π^和上一次结果会有不同,也即结果具有随机性。一般地,假设随机变量X XX的期望为θ \thetaθ,方差为σ 2 \sigma^2σ2。产生随机变量X XX的N NN个独立同分布随机数X i , i = 1 , 2 , ⋯ , N X_i,i=1,2,\cdots,NXi,i=1,2,⋯,N,用样本均值X N ‾ = 1 N ∑ i = 1 N X i \overline{X_N}=\frac{1}{N}\sum\limits_{i=1}^{N}X_iXN=N1i=1∑NXi估计θ \thetaθ,由中心极限定理可知X N ‾ \overline{X_N}XN近似服从N ( θ , σ 2 N ) N(\theta,\frac{\sigma^2}{N})N(θ,Nσ2),于是随机模拟误差幅度约为O ( 1 N ) ( N → ∞ ) O(\frac{1}{\sqrt{N}})(N\to\infty)O(N1)(N→∞),因此为了增加一位小数的精度,即误差减小到原来的1 10 \frac{1}{10}101,重复试验次数需要增加都爱原来的100 100100倍。
但是由于随机模拟方法对维数增加不敏感,因此维数的增加造成的影响很小(在计算定积分时,如果使用传统数值算法,维数增加会造成计算时间呈指数增加),因此蒙特卡罗方法被广泛应用到各个领域。本文将探讨其用于求解积分(主要是一维积分,二维或者更高维的积分可以类比推广)的用途,以及各种减小其方差的方法,并使用MATLAB进行模拟计算。
首先给出基本代码
clear, clc, tic
f1 = @(x) sqrt(1-x.^2);
f2 = @(x) sin(x) ./ x;
f3 = @(x) exp(x);
func = f3;
blk = [0, 1];
testTimes = 1000000;
realRes = integral(func, blk(1), blk(2));
calcRes = zeros(1, 100);
error = zeros(1, 100);
%=====================================%
% 此处为各个方法对应的代码
%=====================================%
fprintf("估算值:%.16f\n", mean(calcRes));
fprintf("误差: %.16f\n", mean(error));
fprintf("方差: %.16f\n", var(error));
toc
随机投点法
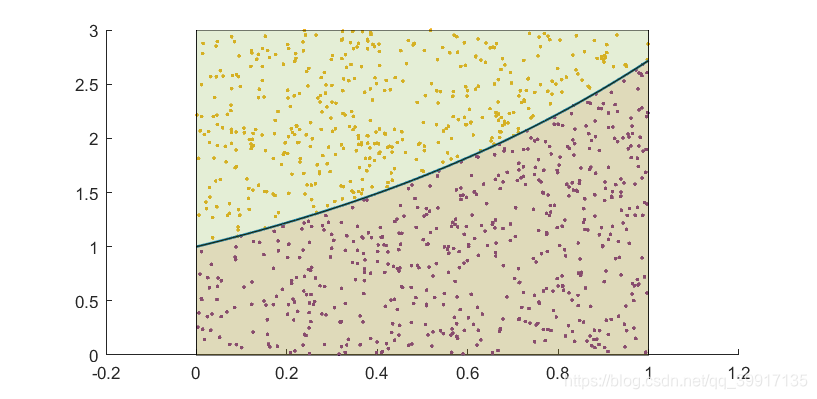
设被积函数在积分区间[ a , b ] [a,b][a,b]上有界,不妨设为[ 0 , M ] [0,M][0,M],则求积分I = ∫ a b h ( x ) d x I=\int_a^b h(x)\mathrm{d}xI=∫abh(x)dx相当于计算曲线h ( x ) h(x)h(x)下的区域D = { ( x , y ) : a ≤ x ≤ b , 0 ≤ y ≤ h ( x ) } D=\{(x,y):a\le x\le b,~0\le y \le h(x)\}D={(x,y):a≤x≤b, 0≤y≤h(x)}的面积,在此区域G = [ a , b ] × [ 0 , M ] G=[a,b]\times[0,M]G=[a,b]×[0,M]上做均匀抽样N NN次,得到随机样本点D 1 , D 2 , ⋯ , D N = ( X i , Y i ) , i = 1 , 2 , ⋯ , N . D_1,D_2,\cdots,D_N=(X_i,Y_i),~i=1,2,\cdots,N.D1,D2,⋯,DN=(Xi,Yi), i=1,2,⋯,N. 令
η i = { 1 , D i ∈ D 0 , D i ∉ D , i = 1 , 2 , ⋯ , N \eta_i=\left\{ \begin{array}{rcl} 1 &,& D_i\in D \\ 0 &,& D_i\notin D \end{array}\right., i=1,2,\cdots,Nηi={10,,Di∈DDi∈/D,i=1,2,⋯,N
则η i \eta_iηi独立同分布于B ( 1 , p ) B(1,p)B(1,p),其中
p = P ( D i ∈ D ) = S D S G = I M ( b − a ) p=P(D_i\in D)=\frac{S_D}{S_G}=\frac{I}{M(b-a)}p=P(Di∈D)=SGSD=M(b−a)I
得到随机的投点D 1 , D 2 , ⋯ , D N D_1,D_2,\cdots,D_ND1,D2,⋯,DN后,由强大数定律可知,当N → ∞ N\to\inftyN→∞时,其落入曲线下方区域D DD的概率p ^ \hat{p}p^趋近于p pp,因此当N NN足够大的时候,可以通过N NN个样本点出现在曲线下方的频率来求得积分
I ≈ I ^ = p ^ M ( b − a ) I\approx\hat{I}=\hat{p}M(b-a)I≈I^=p^M(b−a)
同时可以论证I ^ \hat{I}I^的误差为O p ( 1 N ) O_p(\frac{1}{\sqrt{N}})Op(N1),也就是说,若采取随机投点法,要提高一位精度,则需要100倍的样本数量。
根据上面论证编写程序:
result = zeros(1, testTimes);
for k = 1:100
x = unifrnd(blk(1), blk(2), 1, testTimes);
y = unifrnd(1, 3, 1, testTimes);
result = y < func(x);
calcRes(k) = sum(result) / testTimes * 2 + 1;
error(k) = abs(calcRes(k)-realRes);
end
期望积分法
可以看到,随机投点法能够大致估计出积分取值,但是其精度很低,并且需要增加100倍才能提高一位的精度。另一种效率更高的求定积分的方法是利用期望值的估计。设U ∼ U ( a , b ) U\sim U(a,b)U∼U(a,b),则
E [ h ( U ) ] = ∫ a b h ( u ) 1 b − a d u = I b − a , ⇒ I = ( b − a ) ⋅ E h ( U ) E[h(U)]=\int_a^b h(u)\frac{1}{b-a}\mathrm{d}u=\frac{I}{b-a},\Rightarrow I=(b-a)\cdot Eh(U)E[h(U)]=∫abh(u)b−a1du=b−aI,⇒I=(b−a)⋅Eh(U)
若N NN个样本U 1 , U 2 , ⋯ , U N U_1,U_2,\cdots,U_NU1,U2,⋯,UN独立同分布于U ( a , b ) U(a,b)U(a,b)分布,则由强大数定律,当N → ∞ N\to \inftyN→∞时
E [ h ( U ) ] = 1 N ∑ i = 1 N h ( U i ) = I ^ b − a E[h(U)]=\frac{1}{N}\sum\limits_{i=1}^N h(U_i)=\frac{\hat{I}}{b-a}E[h(U)]=N1i=1∑Nh(Ui)=b−aI^
因此I II的估计值为
I ^ = b − a N ∑ i = 1 N h ( U i ) \hat{I}=\frac{b-a}{N}\sum\limits_{i=1}^N h(U_i)I^=Nb−ai=1∑Nh(Ui)
可以证明,此方法的误差仍然为O p ( 1 N ) O_p(\frac{1}{\sqrt{N}})Op(N1),但是方差比随机投点法小。
据此编写程序:
result = zeros(1, testTimes);
for k = 1:100
x = unifrnd(blk(1), blk(2), 1, testTimes);
result = func(x) / testTimes;
calcRes(k) = sum(result);
error(k) = abs(calcRes(k)-realRes);
end
重要抽样法
被积函数h ( x ) h(x)h(x)可能在各处的取值差异很大,如果直接使用平均值估计积分,即均匀采样,很多样本值较小的地方,尤其是接近0 00的地方会浪费较多的点,这样会导致方差比较大,因此考虑非均匀抽样,在∣ h ( x ) ∣ |h(x)|∣h(x)∣大的地方采集更多的点,∣ h ( x ) ∣ |h(x)|∣h(x)∣小的地方采集更少的点,这样可以更有效地利用样本。
设非均匀采样密度函数为g ( x ) g(x)g(x),即在相应x xx处以g ( x ) g(x)g(x)的概率密度进行采样,这里g ( x ) g(x)g(x)的形状与h ( x ) h(x)h(x)类似。现有N NN个数据点X 1 , X 2 , ⋯ , X N X_1,~X_2,\cdots,X_NX1, X2,⋯,XN独立同分布于g ( x ) g(x)g(x),令
η i = h ( X i ) g ( X i ) , i = 1 , 2 , ⋯ , N . \eta_i=\frac{h(X_i)}{g(X_i)},~i=1,2,\cdots,N.ηi=g(Xi)h(Xi), i=1,2,⋯,N.
则
E η = ∫ C h ( x ) g ( x ) g ( x ) d x = ∫ C h ( x ) d x = I E\eta=\int_C\frac{h(x)}{g(x)}g(x)\mathrm{d}x=\int_C h(x)\mathrm{d}x=IEη=∫Cg(x)h(x)g(x)dx=∫Ch(x)dx=I
因此可以用{ η i , i = 1 , 2 , ⋯ , N } \{\eta_i,~i=1,2,\cdots,N\}{ηi, i=1,2,⋯,N}的样本均值来估计I II,即
I = E η = 1 N ∑ i = 1 N h ( X i ) g ( X i ) I=E\eta=\frac{1}{N}\sum\limits_{i=1}^N \frac{h(X_i)}{g(X_i)}I=Eη=N1i=1∑Ng(Xi)h(Xi)
以h ( x ) = e x h(x)=e^xh(x)=ex为例,对被积函数h ( x ) = e x h(x)=e^xh(x)=ex做泰勒展开得
h ( x ) = e x = 1 + x + x 2 2 + ⋯ . h(x)=e^x=1+x+\frac{x^2}{2}+\cdots.h(x)=ex=1+x+2x2+⋯.
取
g ( x ) = c ( 1 + x ) = 2 3 ( 1 + x ) . g(x)=c(1+x)=\frac{2}{3}(1+x).g(x)=c(1+x)=32(1+x).
使用逆变换法产生满足g ( x ) g(x)g(x)密度函数的随机数,g ( x ) g(x)g(x)的分布函数G ( x ) G(x)G(x)的反函数为
G − 1 ( y ) = 1 + 3 y − 1 , 0 < y < 1. G^{-1}(y)=\sqrt{1+3y}-1,~0<y<1.G−1(y)=1+3y−1, 0<y<1.
因此,取U i U_iUi独立同分布于U ( 0 , 1 ) , i = 1 , 2 , ⋯ , N U(0,1),~i=1,2,\cdots,NU(0,1), i=1,2,⋯,N,则X i = 1 + 3 U i − 1 X_i=\sqrt{1+3U_i}-1Xi=1+3Ui−1服从概率密度g ( x ) g(x)g(x)的分布
因此根据重要抽样法,求积分的式子为
I ^ = 1 N ∑ i = 1 N e X i 2 3 ( 1 + X i ) \hat{I}=\frac{1}{N}\sum\limits_{i=1}^N\frac{e^{X_i}}{\frac{2}{3}(1+X_i)}I^=N1i=1∑N32(1+Xi)eXi
据此编写程序如下
result = zeros(1, testTimes);
for k = 1:100
u = unifrnd(blk(1), blk(2), 1, testTimes);
x = sqrt(1+3*u) - 1;
result = exp(x) ./ (1 + x) * 1.5 / testTimes;
calcRes(k) = sum(result);
error(k) = abs(calcRes(k)-realRes);
end
控制变量法
已知两个随机变量X XX和Y YY。其中要求的是X XX的期望,若不通过Y YY来求X XX的期望,则可以从X XX中抽取N NN个独立样本值X 1 , X 2 , ⋯ , X N X_1,X_2,\cdots,X_NX1,X2,⋯,XN,然后计算X ‾ = 1 N ∑ i = 1 N X i \overline{X}=\frac{1}{N}\sum\limits_{i=1}^N X_iX=N1i=1∑NXi来估计E X . EX.~EX. 若通过Y YY来求X XX的期望,且满足
E Y = 0 , C o v ( X , Y ) < 0 EY=0,~Cov(X,Y)<0EY=0, Cov(X,Y)<0
令Z ( b ) = X + b Y Z(b)=X+bYZ(b)=X+bY,则
E Z ( b ) = E X V a r ( Z ( b ) ) = V a r ( X ) + 2 b C o v ( X , Y ) + b 2 V a r ( Y ) EZ(b)=EX\\ Var(Z(b))=Var(X)+2bCov(X,Y)+b^2Var(Y)EZ(b)=EXVar(Z(b))=Var(X)+2bCov(X,Y)+b2Var(Y)
不难得到,当
b = − C o v ( X , Y ) V a r ( Y ) = − ρ X , Y V a r ( X ) V a r ( Y ) b=-\frac{Cov(X,Y)}{Var(Y)}=-\rho_{X,Y}\sqrt{\frac{Var(X)}{Var(Y)}}b=−Var(Y)Cov(X,Y)=−ρX,YVar(Y)Var(X)
时,Z ( b ) Z(b)Z(b)有最小方差
V a r ( Z ( b ) ) = ( 1 − ρ X , Y 2 ) V a r ( X ) ≤ V a r ( X ) Var(Z(b))=(1-\rho_{X,Y}^2)Var(X)\le Var(X)Var(Z(b))=(1−ρX,Y2)Var(X)≤Var(X)
因此,只要X XX和Y YY的相关系数不等于0 00,则可以减小方差,。
以h ( x ) = e x h(x)=e^xh(x)=ex为例,先求积分I = ∫ 0 1 e x d x I=\int_0^1 e^x\mathrm{d}xI=∫01exdx,理论值为e − 1 e-1e−1,若使用控制变量法,设U ∼ U ( 0 , 1 ) U\sim U(0,1)U∼U(0,1),且X = e U , Y = U − 1 2 X=e^U,~Y=U-\frac{1}{2}X=eU, Y=U−21,则可以求得
E Y = 0 , C o v ( X , Y ) ≈ 0.14086 , V a r ( Y ) = 1 12 b = − C o v ( X , Y ) V a r ( Y ) ≈ − 1.690 EY=0,~Cov(X,Y)\approx 0.14086,~Var(Y)=\frac{1}{12}\\ b=-\frac{Cov(X,Y)}{Var(Y)}\approx -1.690EY=0, Cov(X,Y)≈0.14086, Var(Y)=121b=−Var(Y)Cov(X,Y)≈−1.690
于是抽取N NN个均匀分布值U 1 , U 2 , ⋯ , U N U_1, U_2, \cdots,U_NU1,U2,⋯,UN并根据大数定律对Z i = e U i − 1.690 ( U i − 1 12 ) Z_i=e^{U_i}-1.690(U_i-\frac{1}{12})Zi=eUi−1.690(Ui−121)求期望可以得到
I ^ = 1 N ∑ i = 1 N [ e U i − 1.690 ( U i − 1 12 ) ] . \hat{I}=\frac{1}{N}\sum\limits_{i=1}^N\left[e^{U_i}-1.690(U_i-\frac{1}{12})\right].I^=N1i=1∑N[eUi−1.690(Ui−121)].
根据上述分析编写代码如下
func_new = @(x) func(x) - 1.690309 * (x - 0.5);
result = zeros(1, testTimes);
for k = 1:100
x = unifrnd(blk(1), blk(2), 1, testTimes);
result = func_new(x) / testTimes;
calcRes(k) = sum(result);
error(k) = abs(calcRes(k)-realRes);
end
对偶变量法
设F ( x ) F(x)F(x)为连续分布函数,U ∼ U ( 0 , 1 ) , X = F − 1 ( U ) , Y = F − 1 ( 1 − U ) , Z = X + Y 2 U\sim U(0,1),~X=F^{-1}(U),~Y=F^{-1}(1-U),~Z=\frac{X+Y}{2}U∼U(0,1), X=F−1(U), Y=F−1(1−U), Z=2X+Y,则显然X XX与Y YY同分布,并且可以得到C o v ( X , Y ) ≤ 0 Cov(X,Y)\le 0Cov(X,Y)≤0,因此
V a r ( Z ) = 1 4 [ V a r ( X ) + V a r ( Y ) + 2 C o v ( X , Y ) ] = 1 2 [ V a r ( X ) + C o v ( X , Y ) ] ≤ 1 2 V a r ( X ) . \begin{array}{rcl} Var(Z) &=& \frac{1}{4}\left[Var(X)+Var(Y)+2Cov(X,Y)\right]\\ &=& \frac{1}{2}\left[Var(X)+Cov(X,Y)\right]\\ &\le& \frac{1}{2}Var(X). \end{array}Var(Z)==≤41[Var(X)+Var(Y)+2Cov(X,Y)]21[Var(X)+Cov(X,Y)]21Var(X).
因此,抽取N NN个样本点U 1 , U 2 , ⋯ , U N U_1,U_2,\cdots,U_NU1,U2,⋯,UN,则可以令
Z i = 1 2 ( F − 1 ( U i ) + F − 1 ( 1 − U i ) ) Z_i=\frac{1}{2}\left(F^{-1}(U_i)+F^{-1}(1-U_i)\right)Zi=21(F−1(Ui)+F−1(1−Ui))
从而求得积分值。以h ( x ) = e x h(x)=e^xh(x)=ex为例,设U ∼ U ( 0 , 1 ) , X = e U , Y = e 1 − U U\sim U(0,1),~X=e^{U},~Y=e^{1-U}U∼U(0,1), X=eU, Y=e1−U,使用对偶变量法可得积分估计值为
I ^ = 1 N ∑ i = 0 N e U i + e 1 − U i 2 \hat{I}=\frac{1}{N}\sum\limits_{i=0}^N \frac{e^{U_i}+e^{1-U_i}}{2}I^=N1i=0∑N2eUi+e1−Ui
据此编写程序如下:
func_new = @(x) (func(x) + func(1 - x)) / 2;
result = zeros(1, testTimes);
for k = 1:100
x = unifrnd(blk(1), blk(2), 1, testTimes);
result = func_new(x) / testTimes;
calcRes(k) = sum(result);
error(k) = abs(calcRes(k)-realRes);
end
分层抽样法
分层抽样法将积分区域C CC分为若干个子集上的积分,使得在每个子集上的变化不大,分别计算各个子集上的积分再求和,从而提高精确度。
设积分I = ∫ C h ( x ) d x I=\int_Ch(x)\mathrm{d}xI=∫Ch(x)dx可以分解为m mm个不相交的子集C j C_jCj上的积分,即
I = ∫ C h ( x ) d x = ∫ C 1 h ( x ) d x + ∫ C 2 h ( x ) d x + ⋯ + ∫ C m h ( x ) d x I=\int_Ch(x)\mathrm{d}x=\int_{C_1}h(x)\mathrm{d}x+\int_{C_2}h(x)\mathrm{d}x+\cdots+\int_{C_m}h(x)\mathrm{d}xI=∫Ch(x)dx=∫C1h(x)dx+∫C2h(x)dx+⋯+∫Cmh(x)dx
在C j C_jCj上投n j n_jnj个随机点X j i ∼ U ( a j , b j ) , i = 1 , 2 , ⋯ , n j X_{ji}\sim U(a_j,b_j),~i=1,2,\cdots,n_jXji∼U(aj,bj), i=1,2,⋯,nj,则I II的m mm个部分可以分别用期望积分求得,因此可以得到最终积分式子为
I ^ = ∑ j = 1 m b j − a j n j ∑ i = 1 n j h ( X j i ) \hat{I}=\sum\limits_{j=1}^m\frac{b_j-a_j}{n_j}\sum\limits_{i=1}^{n_j}h(X_{ji})I^=j=1∑mnjbj−aji=1∑njh(Xji)
以h ( x ) = e x , I = ∫ 0 1 h ( x ) d x h(x)=e^x,~I=\int_0^1 h(x)\mathrm{d}xh(x)=ex, I=∫01h(x)dx为例,若分层数为2 22,则积分式子可以写成
I = ∫ 0 0.5 e x d x + ∫ 0.5 1 e x d x I=\int_{0}^{0.5}e^x\mathrm{d}x+\int_{0.5}^{1}e^x\mathrm{d}xI=∫00.5exdx+∫0.51exdx
从而根据期望积分法对每一部分进行积分,总共取N NN个点,可以得到
I ^ = 0.5 − 0 N / 2 ∑ i = 1 N / 2 e U 1 i + 1 − 0.5 N / 2 ∑ i = ( N / 2 ) + 1 N e U 2 i \hat{I}=\frac{0.5-0}{N/2}\sum\limits_{i=1}^{N/2}e^{U_{1i}}+\frac{1-0.5}{N/2}\sum\limits_{i=(N/2)+1}^{N}e^{U_{2i}}I^=N/20.5−0i=1∑N/2eU1i+N/21−0.5i=(N/2)+1∑NeU2i
其中U 1 i ∼ U ( 0 , 0.5 ) , U 2 i ∼ U ( 0.5 , 1 ) U_{1i}\sim U(0,0.5),~U_{2i}\sim U(0.5,1)U1i∼U(0,0.5), U2i∼U(0.5,1),根据此方法得到的结果方差可以得到大幅度的减小。
据分析编写代码如下
layer = 10000;
layerStep = 1 / layer;
N = floor(testTimes/layer);
result = zeros(1, layer);
for k = 1:100
x=unifrnd(blk(1), blk(2),1,testTimes);
for i = 1:layer
a = (i - 1) * layerStep;
b = i * layerStep;
x = unifrnd(a, b, 1, N);
result(i) = mean(func(x)) * layerStep;
end
calcRes(k) = sum(result);
error(k) = abs(calcRes(k)-realRes);
end
Metropolis Hasting算法
此算法是一个基本的MCMC(马氏链蒙特卡罗)算法。一般地,对于高维或者取值空间χ \chiχ结构复杂的随机变量X XX,MCMC方法构造取值于χ \chiχ的马氏链,使其平稳分布为X XX的目标分布。模拟此马氏链,抛弃开始的部分抽样值,把剩余部分作为X XX的非独立抽样。非独立抽样的估计效率比独立抽样低。
Metropolis Hasting算法在每一步试探地进行转移(如随机游动),如果转移后能提高状态x t x_txt在目标分布π \piπ中的密度值则接受转移结果,否则以一定的概率决定是转移还是停留不动。具体算法如下:
抽样完成之后,根据获得的状态集合进行求积分。首先将得到的状态集合按照固定的间隔进行统计,统计出现在每个段里面的状态的个数并记录下来。如图所示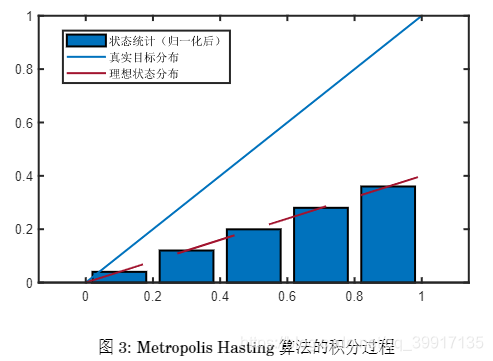
不妨设目标函数为π ( x ) = x \pi(x)=xπ(x)=x,经过Metropolis Hasting算法将状态集合根分成m mm段,每段的中点为x i , i = 1 , 2 , ⋯ , m x_i,~i=1,2,\cdots,mxi, i=1,2,⋯,m,并设每段中出现状态的数目占比(即对出现的次数求概率密度)为n 1 ^ , n 2 ^ , ⋯ , n m ^ \hat{n_1},\hat{n_2},\cdots,\hat{n_m}n1^,n2^,⋯,nm^,并且满足
∑ i = 1 m n i ^ = 1 \sum\limits_{i=1}^{m}\hat{n_i}=1i=1∑mni^=1
显然归一化之后的理想状态分布与目标函数只相差整数倍k kk,当总试验次数N → ∞ N\to\inftyN→∞时,有
n i ^ → 1 k π ( x i ) , i = 1 , 2 , ⋯ , m \hat{n_i}\to \frac{1}{k}\pi(x_i),~i=1,2,\cdots,mni^→k1π(xi), i=1,2,⋯,m
当区间划分得足够细的时候,可以使用矩形法求得目标函数的积分,如
I ≈ ∑ i = 1 m π ( x i ) × 1 − 0 m ≈ ∑ i = 1 m k n i ^ m = k m ∑ i = 1 m n i ^ = k m I \approx\sum\limits_{i=1}^{m}\pi(x_i)\times \frac{1-0}{m} \approx\sum\limits_{i=1}^{m}\frac{k\hat{n_i}}{m} =\frac{k}{m}\sum\limits_{i=1}^{m}\hat{n_i} =\frac{k}{m}I≈i=1∑mπ(xi)×m1−0≈i=1∑mmkni^=mki=1∑mni^=mk
而对于k kk,则在每一段的目标函数值与状态归一化值的比例都近似等于k kk,因此对每一段的比值求平均得到k kk从而减小误差
k ≈ 1 m ( ∑ i = 1 m π ( x i ) x i ^ ) k\approx \frac{1}{m}\left(\sum\limits_{i=1}^m \frac{\pi(x_i)}{\hat{x_i}}\right)k≈m1(i=1∑mxi^π(xi))
从而得到最终的积分值为
I ≈ 1 − 0 m 1 m ( ∑ i = 1 m π ( x i ) x i ^ ) I\approx\frac{1-0}{m}\frac{1}{m}\left(\sum\limits_{i=1}^m \frac{\pi(x_i)}{\hat{x_i}}\right)I≈m1−0m1(i=1∑mxi^π(xi))
算法过程如下:
clear, clc, clf, tic
mu = 2; sigma = 3; % 用于正态函数的模拟
f1 = @(x) sqrt(1-x.^2);
f2 = @(x) sin(x) ./ x;
f3 = @(x) exp(x);
f4 = @(x) 0.3 * exp(-0.2*x.^2) + 0.7 * exp(-0.2*(x - 10).^2);
f5 = @(x) 1 / (sigma * sqrt(2 * pi)) * exp(-(x - mu).^2/(2 * sigma^2));
func = f5;
uniform_sample = @(a, b) a + rand() * (b - a);
num_sample = 1000000; % 总共需要步的步数(个状态)
num_skip = 10000; % 经过该步数之后才算做有效数据
X = zeros(1, num_sample + num_skip);% 初始状态设置为0
for i = 2:(num_sample + num_skip) % 需要num_sample步+num_skip步
xnow = X(i-1);
xnext = uniform_sample(0, 1); % 随机采样的结果,采用(0,1)上的均匀采样
r = min(1, func(xnext)/func(xnow)); % 用于与接收
u = rand();
if (u <= r) % 接收新采样得到的数据作为下一个状态值
X(i) = xnext;
else % 拒绝,并保持当前值
X(i) = xnow;
end
end
plot(1:num_sample, X(num_skip + (1:num_sample)));
% mean(X(num_skip +(1 :num_sample)));
% std(X(num_skip +(1 :num_sample)));
% 将区间分为num_seg个区段,统计落到每个区段上值的个数(histcounts)
num_seg = 50;
[counts, interval] = histcounts(X(num_skip + (1:num_sample)), num_seg);
% 每个区段的中点值
points = (interval(1:end - 1) + interval(2:end)) / 2;
figure(1);clf;
bar(points, counts/num_sample); % 将每个区段的数量绘制出来
x = linspace(0, 1, num_seg); y = func(x);
hold on; plot(x, func(x) / sum(func(x))); % 理论的分布
% 计算模拟积分值与真实积分值并对比
rand_calc = (num_sample ./ counts) * func(points)' / num_seg^2;
real_calc = integral(func, 0, 1);
delta1 = abs(rand_calc - real_calc);
fprintf("rand_calc = %.16f\n", rand_calc);
fprintf("real_calc = %.16f\n", real_calc);
fprintf("积分误差 = %.16f\n", delta1);
toc
% 随机模拟出的分布函数与真实分布函数的比较
F1(1) = 0; F2(1) = 0; % 初始化分布函数的值
for i = 2:num_seg
F1(i) = F1(i-1) + counts(i) / num_sample;
F2(i) = F2(i-1) + y(i) / sum(y);
end
figure(2); clf;
plot(x, [F1', F2']); % 绘制两个分布函数
delta2 = max(F1-F2); % 随机模拟准确度的度量方法之一
fprintf("分布误差 = %.16f\n", delta2);
| 求积分方法 | 结果 | 误差 | 方差 |
|---|---|---|---|
| 随机投点法 | 1.7181937400000005 | 0.0006431297075427 | 0.0000002829013013 |
| 期望积分法 | 1.7182937138487426 | 0.0003736725483337 | 0.0000000688076089 |
| 重要抽样法 | 1.7183052639908123 | 0.0001332292199415 | 0.0000000079561180 |
| 控制变量法 | 1.7182822454501496 | 0.0000484695418992 | 0.0000000015568030 |
| 对偶变量法 | 1.7182892445766689 | 0.0000486468709196 | 0.0000000013180232 |
| 分层抽样法 | 1.7182818289993276 | 0.0000000427815156 | 0.0000000000000012 |
| MH算法 | 1.7179493974835627 | 0.0003324309754824 |
可见,在这几种方法中,对于求解h ( x ) = e x h(x)=e^xh(x)=ex在( 0 , 1 ) (0,1)(0,1)上的定积分,当实验次数为1000000 10000001000000次时,分层抽样法的效率是最高的,误差及其方差都是最小的。当然,也可以尝试使用不同的重点抽样函数以减小方差,使用分层抽样法和控制变量法或者对偶变量法结合,重点抽样法和MH算法结合等等。
Gibbs抽样
最后再讨论一下Gibbs抽样算法,因为此算法一般用于二维或者更高维分布的模拟,所以不在上面一维积分处列出,但是Gibbs算法理论上也可以用于求一维积分,不过这样的效率就会非常低。
一般的MCMC抽样每一步先尝试移动,然后根据新状态是否看尽目标分布来决定是接受还是拒绝该状态的值,因此会出现多次尝试仍然未移动的情况,这样会降低抽样效率。而Gibbs抽样则使用条件分布的抽样来代替这种全概率式的抽样,对于多维Gibbs抽样,其基本思路如下
现有条件概率分布为两个正态分布,它们分别服从N ( 5 , 1 ) , N ( − 1 , 4 ) N(5,1),~N(-1,4)N(5,1), N(−1,4),相关系数为ρ \rhoρ,根据Gibbs算法进行抽样,最终得到模拟出来的边缘分布,联合分布以及真实分布如图
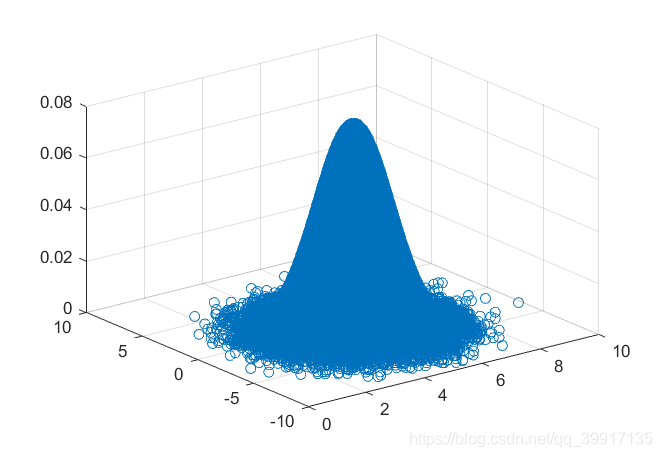
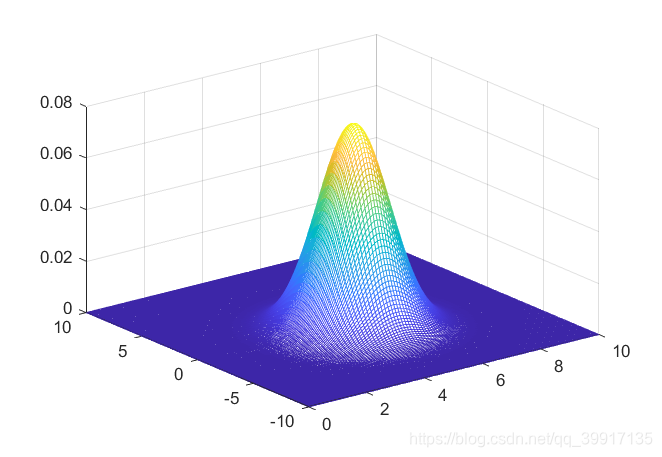
现在考虑将相关系数设置成0 00,则两个边缘分布是相互独立的。根据Gibbs算法可以产生服从一维正态分布的状态集合,而根据此状态集合可以使用和前面Metropolis Hasting求积分时同样的算法,从而求得正态分布的积分。经MATLAB验证,当试验次数为100000 100000100000次时,模拟一次计算得到0.993198818520657 0.9931988185206570.993198818520657(理论值为1 11)的积分值,可见效率显然比不上其他算法。
代码如下:
clear,clc,clf
pyx=@(x,m1,m2,s1,s2,rho) normrnd(m2+rho*s2/s1*(x-m1),sqrt((1-rho^2)*s2^2));
pxy=@(y,m1,m2,s1,s2,rho) normrnd(m1+rho*s1/s2*(y-m2),sqrt((1-rho^2)*s1^2));
bixy=@(x,y,m1,m2,s1,s2,rho) 1/(2*pi*s1*s2*sqrt(1-rho^2)).*exp(-1/(2*(1-rho^2)).*((x-m1).*(x-m1)/s1^2-2*rho*(x-m1).*(y-m2)/s1/s2+(y-m2).*(y-m2)/s2^2));
N=10000;
m1=5;
m2=-1;
s1=1;
s2=2;
rho=0;
mu=[m1, m2];
Sigma=[s1^2,rho*s1*s2;rho*s1*s2,s2^2]; % 协方差矩阵
x_res=zeros(1,N); % 初始化
y_res=zeros(1,N);
z_res=zeros(1,N);
y=m2; % 初始值
for i=1:N
x=pxy(y,m1,m2,s1,s2,rho);
y=pyx(x,m1,m2,s1,s2,rho);
z=mvnpdf([x,y],mu,Sigma); % 根据采得数据计算联合分布值
x_res(i)=x;
y_res(i)=y;
z_res(i)=z;
end
num_bins=100; % 将状态集合分成多少段进行统计
func=@(x) 1/sqrt(2*pi)/s1*exp(-(x-m1).^2/2/s1^2);
[x_counts,x_interval]=histcounts(x_res,num_bins); % 统计每一段状态出现次数
x_points = (x_interval(1:end - 1) + x_interval(2:end)) / 2;
tmp=find(x_counts~=0); % 有些状态出现次数为0,避免其出现在分母上
rand_calc = (N ./ x_counts(tmp)) * func(x_points(tmp))' / length(tmp)...
* (x_interval(2)-x_interval(1))
figure(1); clf; bar(x_points, x_counts/N);
% histogram(x_res,num_bins,'normalization','pdf'); % 绘制概率密度
% histogram(y_res,num_bins,'normalization','pdf');
figure(2); clf; scatter3(x_res,y_res,z_res) % 绘制联合分布图
figure(3); clf; p(m1,m2,s1,s2,rho,0,10,-10,20); % 真实分布
function p(m1,m2,s1,s2,rho,xmin,a,ymin,b )%真实分布
bixy=@(x,y,m1,m2,s1,s2,rho) 1/(2*pi*s1*s2*sqrt(1-rho^2)).*exp(-1/(2*(1-rho^2)).*((x-m1).*(x-m1)/s1^2-2*rho*(x-m1).*(y-m2)/s1/s2+(y-m2).*(y-m2)/s2^2));
x=xmin:0.1:xmin+a;
y=ymin:0.1:ymin+b;
[X,Y]=meshgrid(x,y); % 产生网格数据并处理
p = bixy(X, Y, m1, m2, s1, s2, rho);
figure(3); clf; mesh(X,Y,p)
end
参考文献
- 李东风. 统计计算[M]. 高等教育出版社, 2017.
- 洪志敏,白如玉,闫在在,陈君洋.二重积分的蒙特卡罗数值算法[J].数学的实践与认识,2015,45(20):266-271.
- MCMC(四)Gibbs采样