目录
第一章
算法引入
算法是独立存在的一种解决问题的方法和思想
1,如果 a+b+c=1000,且a^2+b^2=c^2(a,b,c为自然数),如何求出所有a、b、c可能的组合?
枚举法(一个一个去试)
a=0,b=0,c=0------不满足a+b+c=1000
试a=0,b=0,c=4------不满足a+b+c=1000
试a=0,b=1,c=0~1000
import time
start_time = time.time()
for a in range(0,1001):
for b in range(0,1001):
for c in range(0,1001):
if a+b+c==1000 and a**2 +b**2 == c**2:
print("a,b,c:%d,%d,%d" % (a,b,c))
#基本步骤数量 T=1000*1000*1000*2 ,T(n)=n^3 * 2 = O(n^3)
end_time = time.time()
print("time:%d"% (end_time-start_time))
print("finished")算法的特征:
输入可以有可以没有,输出至少有一个,有穷性:算法在有限的步骤可接受的时间范围内可以自动结束,确定性:实现的每一个步骤都有确定含义,可行性:算法的每一步都是可行的
c=1000-a-b 不再对c进行试探------快很多
import time
start_time = time.time()
for a in range(0,1001):
for b in range(0,1001):
c=1000-a-b
if a**2 +b**2 == c**2:
print("a,b,c:%d,%d,%d" % (a,b,c))
#基本数量步骤 T(n) = n*n*(1+max(1,0)) = n^2 * 2 = O(n^2)
end_time = time.time()
print("time:%d"% (end_time-start_time))
print("finished")时间复杂度与大O表示法
算法效率衡量:
单靠时间不客观准确,离不开计算机的执行环境---------时间复杂度(基本运算数量)
大“O”记法:
计算规模问题----------数量级,渐进函数
T(n)=n^3 * 2,T(n)=n^3 * 10
g(n)=n^3
T(n)=g(n)
最坏时间复杂度与计算规则
最坏时间复杂度
算法完成工作最少需要多少基本操作,即最优时间复杂度
算法完成工作最多需要多少基本操作,即最坏时间复杂度-------是一种保证,在多少步之内能完成所有的操作
算法完成工作平均需要多少基本操作,即平均时间复杂度
在没有特殊说明时,我们所分析的算法的时间复杂度都是指最坏时间复杂度
计算规则
控制程序流程:
顺序--------时间复杂度按加法计算
循环--------时间复杂度按乘法计算
条件--------分支结构,时间复杂度取最大值
判断一个算法的效率时,往往只需要关注操作数量的最高次项,其它次要项和常数项可以忽略----大O记数法
常见时间复杂度与大小关系
常见时间复杂度:
12 ------- O(1) 常数阶
5log2n+20 ------- O(logn) 对数阶
2n+3 ------- O(n) 线性阶
2n+3nlog2n+19 ------- O(nlogn) nlogn阶
3n^2+2n+1 ------- O(n^2) 平方阶
6n^3+2n^2+3n+4 ------- O(n^3) 立方阶
2^n ------- O(2^n) 指数阶
经常将log2n(以2为底的对数)简写成logn
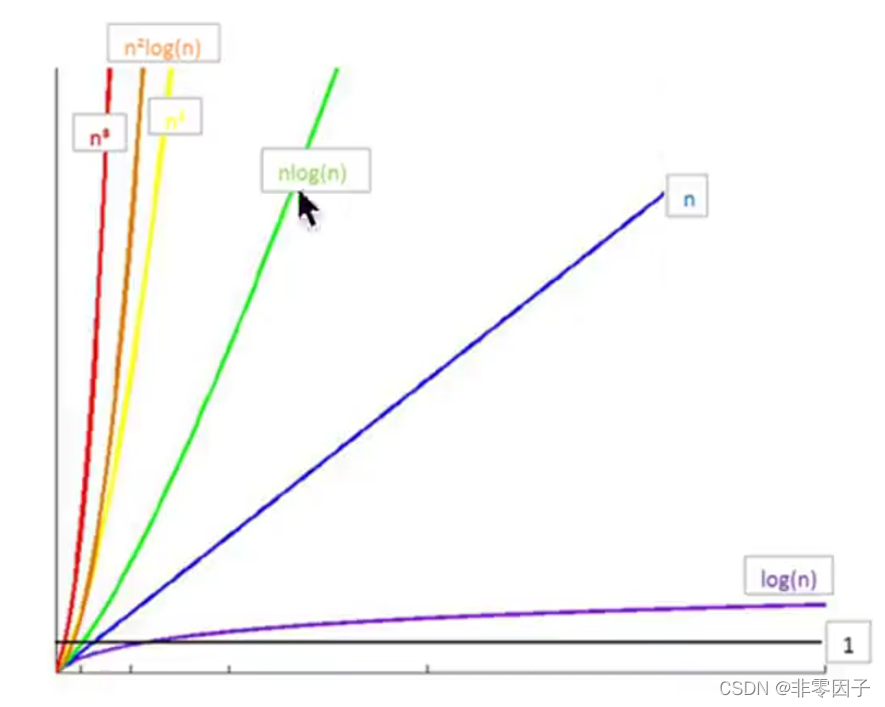
所消耗的时间从小到大:
O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)
代码执行时间测量模块
基本步骤:不会进行函数调用
timeit 测试模块:测试代码执行速度,需要给代码封装成计时器
class timeit.Timer(stmt='pass',setup='pass',timer=<timer function>)
Timer是测量小段代码执行速度的类。
stmt参数是要测试的代码语句(statment);
setup参数是运行代码时需要的设置;
timer参数是一个定时器函数,与平台有关。
timeit.Timer.timeit(number=1000000)
Timer类中测试语句执行速度的对象方法。number参数是测试代码时的测试次数,默认为1000000次。方法返回执行代码的平均耗时,一个float类型的秒数。
python列表类型不同操作的时间效率
文件名和包名不要重名
python2 中 range返回的是普通的对象
python3 中 range返回的是可迭代的对象
list 和 dict 不能算作基本操作类型,算是python 封装好的
# coding:utf-8
from timeit import Timer
# 使用不同的产生列表的方法,测算它们的时间
def test1(): # 叠加,只接受单个元素
li = []
for i in range(10000):
li .append(i)
def test2(): # 加
li = []
for i in range(10000):
li =li + [i]
def test3(): # 列表生成器
li = [i for i in range(10000)]
def test4(): # list 转换------------------最快
li = list(range(10000))
def test5(): # 列表扩充,可扩充多个元素
li = []
for i in range(10000):
li.extend([i]) # li + =[i]
timer1 = Timer("test1()","from __main__ import test1")
print("append:",timer1.timeit(1000))
timer2 = Timer("test2()","from __main__ import test2")
print("+:",timer2.timeit(1000))
timer3 = Timer("test3()","from __main__ import test3")
print("[i for i in range]:",timer3.timeit(1000))
timer4 = Timer("test4()","from __main__ import test4")
print("list(range()):",timer4.timeit(1000))
timer5 = Timer("test5()","from __main__ import test5")
print("extend:",timer5.timeit(1000))
def test6(): # append是从队尾追加------------比往头部加快的多
li = []
for i in range(10000):
li.append([i])
def test7(): # insert 0 始终从列表头追加
li = []
for i in range(10000):
li.insert(0,i)
timer6 = Timer("test6()","from __main__ import test6")
print("append:",timer6.timeit(1000))
timer7 = Timer("test7()","from __main__ import test7")
print("insert(0):",timer7.timeit(1000))python列表与字典操作的时间复杂度
list内置操作的时间复杂度
indexx[] O(1)---索引取值(一步就能达到),index assingment O(1)---按索引方式赋值
append O(1)---在尾部追加
pop() O(1)---从尾部往外弹,pop(i) O(n)---从指定位置弹出(最坏从头弹出,n为列表长度)
insert(i,item) O(n)---在指定位置插入元素
del operator O(n)---删除,代表一个元素,一个元素都要清空
iteration O(n)---迭代
contains(in) O(n)---查找,使用in操作符判断元素是否在列表中
get slice[x:y] O(k)---取切片,从x取到y前一个位置,只跟x,y之间的距离k有关,del slice O(n)---删除切片,后面元素往前移,整体前移复杂度为n
set slice O(n+k)---切片赋值,把切片中的元素删掉O(n),把第二个列表中的元素k补充上去
reverse O(n)---逆置
concatenate O(k)---加号,把两个列表加到一起,第二个列表中的k个元素添加到第一个列表的尾
sort O(nlogn)---排序(保持疑问)
multiply O(nk)---乘法
dict内置操作的时间复杂度
copy O(n)---复制,把所有元素在全部生成一份,get item O(1)---取值,set item O(1)---设置
delete item O(1)---删除字典的一个键,contains(in) O(1)---包含,iteration O(n)---迭代
数据结构
有一堆数据怎么组成起来?
可以使用列表,元组,字典等形式对数据进行存储。不同形式需要不同的搜索方法
数据结构就是对基本数据元素的一次封装
程序=数据结构+算法
算法是为了解决实际问题而设计的,数据结构是算法需要处理的问题载体
集合:列表[],元组("",""),字典{"":"","":""},site
name age hometown
[
("zhangsan",24,"beijing"),
("zhangsan",24,"beijing"),
("zhangsan",24,"beijing"),
]
for stu in stus:
if stu(0) == "zhangsan":# 遍历列表
[
{
"name":"zhangsan",
"age":23,
"hometown":"beijing"
},
]
{
"zhangsan":{
"age":24,
"hometown":""
},
}
stus["zhangsan"] # 查找字典抽象数据类型(Abstract Data Type)
指的是把原有的基本数据,和这个数据所支持的基本操作放到一起,作为一个整体。
class stus(object):
def adds(self):
def pop:
def sort
def modify
# 数据归为类stus,有四种操作类型