DFT的共轭对称性及应用

实验二 DFT的共轭对称性及应用

一、【实验目的】

1.掌握实序列的DFT共轭对称性的特点，

2.学习应用实序列DFT的共轭对称性构建频域序列以保证时域序列为实数的方法；

二、【实验原理】

1.DFT的共轭对称性

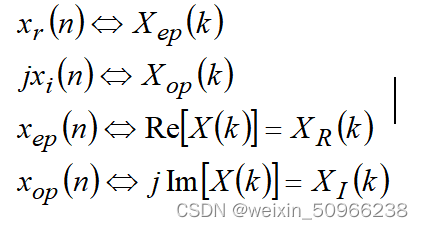
其中：

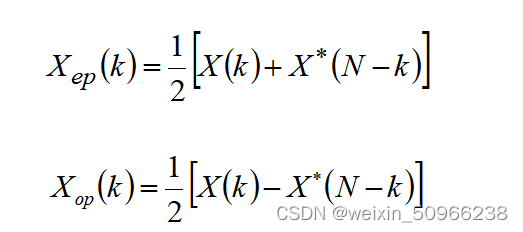
2.有限长实序列的DFT的共轭对称性

 三、【实验内容】

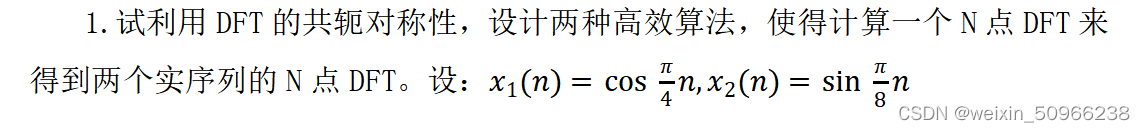
实验代码如下：

实验结果如下：

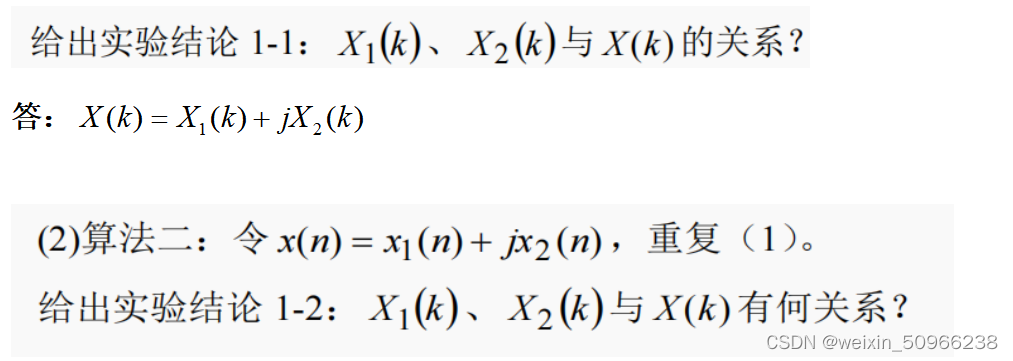
 实验代码如下：

clc,clear,close all

N=16;

n=0:N-1;

k=0:2*pi/N:(2*pi-2*pi/N);

xn1=cos(pi*n/4);

xn2=sin(pi*n/8);

xn=xn1+xn2;

xk=fft(xn,N);

xk1=real(xk);

xk2=j*imag(xk);

xn11=ifft(xk1,N);%反变换

xn21=ifft(xk2,N);%反变换

subplot(321);

stem(n,xn1);

grid on;



title('x1(n)的曲线');

xlabel('n');

ylabel('xn1');

axis([0 16 -1 1]);

subplot(322);

stem(n,xn2);

grid on;



title('x2(n)的曲线');

xlabel('n');

ylabel('xn2');

axis([0 16 -1 1]);



subplot(323);

stem(k/pi,xk1);

grid on;

title('x1(n)的幅频特性曲线');

xlabel('k/pi');

ylabel('X1(K))');

axis([0 2 -10 10]);



subplot(324);

stem(k/pi,imag(xk2));

grid on;

title('x2(n)的幅频特性曲线');

xlabel('k/pi');

ylabel('X2(K)');

axis([0 2 -10 10]);



subplot(325);

stem(n,xn11,'r');

grid on;

title('x11(n)的曲线');

xlabel('n');

ylabel('xn11');

axis([0 16 -1 1]);



subplot(326);

stem(n,xn21,'r');

grid on;

title('x21(n)的曲线');

xlabel('n');

ylabel('xn21');

axis([0 16 -1 1]);

实验结果如下图所示：

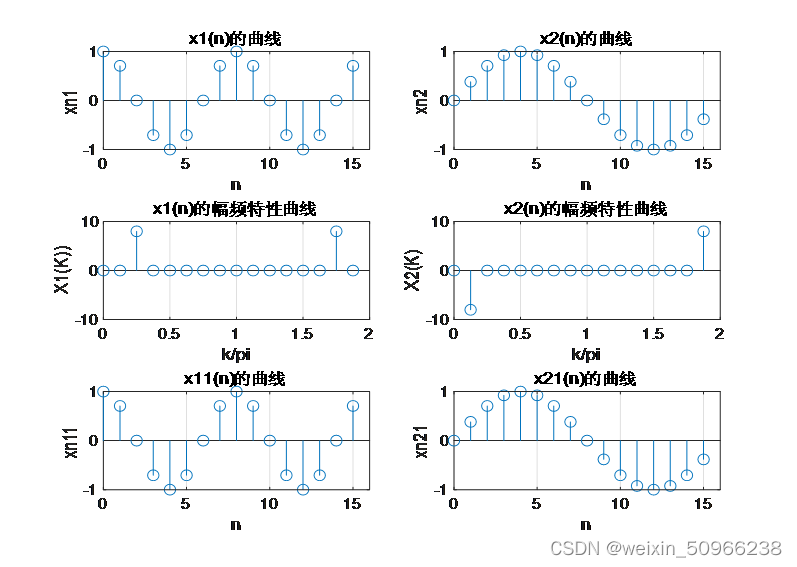
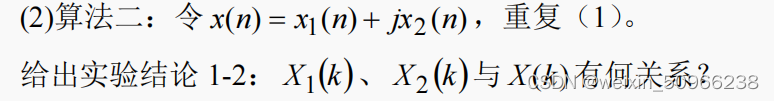
2.有限长实序列的DFT的共轭对称性

由有限长实序列的DFT的共轭对称性可知，频域成共轭对称的序列作IDFT后为实序列，而实数的发送可以大大简化发送设备。OFDM正是利用这一特性 来保证发往信道的序列为实数序列的。

按要求编程完成以下内容：

1. 求频域序列Xk；并给出Xk的实部与虚部图；

实验代码如下：

clc,clear,close all;



n = 0:1:15;

XK_in=[1+1i,-3-1i,-3+3*1i,-1-3*1i];

XK_in2=conj(flip(XK_in));



Xk = [0,XK_in,0,0,0,0,0,0,0,XK_in2]



subplot(2,2,1);

stem(n,real(Xk));

grid on

title("Xk 实部");



subplot(2,2,2)

stem(n,imag(Xk))

grid on

title("Xk 虚部");



xn = ifft(Xk, 16);



subplot(2,2,3);

stem(n,real(xn));

grid on

title("xn 实部");



subplot(2,2,4)

stem(n,imag(xn))

grid on

title("xn 虚部");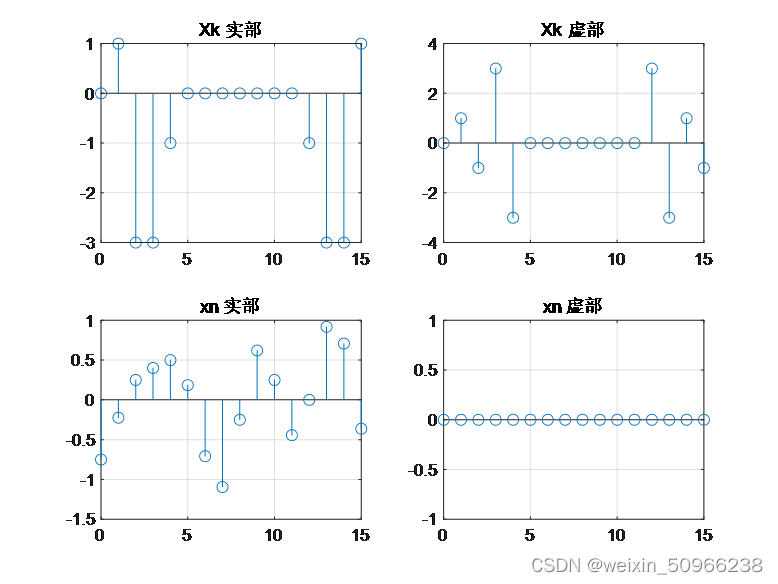

实验结论2-1：说明Xk的实部与虚部各有何特点；

答：实部关于N/2对称，虚部关于N/2成 π 相位差对称。说明是否为实数序列，可以用的实部与虚部图来说明。由的序列图可知，是为实数序列。

四、[思考题]

1.对序列 x(n) ，如何通过计算 N2点DFT而得到N点DFT？

若为长度为N的实序列，则由可以得出，当N为偶数时，只需计算X(k)的前面N/2+1点，而N为奇数时，只需计算X(k)的前面(N+1)/2点，其他点可由得出。减少了一半的计算量。对于任意x(n),可由基2FFT算法，对x(n)进行奇偶序列划分来求DFT。