背景知识回顾

之前的文章中讲了字符串匹配问题中的单模匹配问题，即从一段文本串中找到另一个字符串是否出现过。

母串(文本串)是指要从哪个字符串中查找，模式串指的是要查找哪个字符。

之后介绍了比较经典的暴力匹配算法、KMP匹配算法、Sunday算法、shift_and匹配算法。

1. Leetcode 459: 重复的子字符串

题目链接

解题思路1：暴力查找匹配。循环子串出现的第一个位置一定是起始位置。所以尝试找到循环子串出现的第二个起始位置，然后从这个位置开始向后和循环子串进行匹配。

class Solution {
public:
    bool repeatedSubstringPattern(string s) {
        int pos = 0; //循环子串的第一个位置一定是0位置
        char c = s[0]; 

		//每个pos都是尝试寻找的循环子串的第二个位置，从这个位置向后看是否能完全匹配
        while ((pos = s.find(c, pos + 1)) != s.npos) {
            if (s.size() % pos != 0) continue; //pos也等于找到的循环子串的长度
            int flag = 0;  //flag=0表示假设能匹配成功
            for (int i = pos; i < s.size(); ) { 
            //i从pos位置开始依次和s[0:pos]进行比较
            
                for (int j = 0; j < pos; j++) { //s[0:pos]
                    if (s[i] == s[j]) {
                        i++;
                    }else {
                        i++; 
                        flag = 1;  //比较失败则开始查找下一个pos位置
                        break;
                    }
                }
            }
            if (flag == 0) return true;  //比较过程一直顺利的进行了下去
        }
        return false;
    }
};

提交结果：

总结：注意pos的含义，以及c++中内置的s.find, s.npos函数。

解题思路2：可以将题目理解为要找到字符串末尾位置对应的最长公共前后缀。

例如对于字符串$s="abcabc"$, 可以找到其末尾位置的最长公共前缀位置 $j=2$，对应最长公共前缀的长度3 正好能整除 s 的长度，则s可以由子串重复构成。

而寻找最长公共前缀和后缀正好可以用之前讲过的KMP算法中的next数组来实现。next[i]表示以i位置作为最长公共后缀的末尾时，对应的最长公共前缀的索引。

先看代码实现：

class Solution {
public:
    bool repeatedSubstringPattern(string s) {
        int n = s.size(), j = -1;
        vector<int> next(n);
        next[0] = -1;  //-1是一个虚拟索引，表示该位置不存在最长公共前后缀
        //j表示前一个位置的next值
        for (int i = 1; i < n; i++) {
            while (j != -1 && s[j + 1] - s[i]) j = next[j];
            if (s[j + 1] == s[i]) j += 1;
            next[i] = j;
        }
		//以上都是next数组的预计算

        if (next[n - 1] == -1) return false;  
        //末尾位置不存在最长公共前缀，直接返回false
        
        return n % (n - next[n - 1] - 1) == 0;  
        //注意next数组最长公共前后缀时可以相交的。
        //例如s = 'abcabcabc', 则next[n - 1] = 5 对应第二个c的位置
        //n - next[n - 1] - 1 表示最短循环子串的长度
    }
};

总结：主要是以输入字符串作为模式串，实现了一遍next数组的计算，然后根据最短循环子串的长度是否能整除整个字符串的长度，来输出最终结果。

注意代码的最后一行返回的是$n\%(n-next[n-1]-1)==0$, 因为next数组最长公共前后缀时可以相交的。例如$s="abcabcabc",则next[n-1]=5$ 对应第二个c的位置, 然后 $n-next[n-1]-1$ 表示最短循环子串的长度。

代码提交结果：

2. Leetcode 1392: 最长快乐前缀

题目链接

解题思路：题目的意思就是要求整个字符串的最长公共前缀和后缀，也就是KMP算法中next数组对应的含义，next[i]表示以i位置作为最长公共后缀的末尾时，对应的最长公共前缀的索引。

class Solution {
public:
    string longestPrefix(string s) {
        int n = s.size();
        vector<int> next(n);
        next[0] = -1;
        for (int i = 1, j = -1; i < n; i++) {
            while (j != -1 && s[j + 1] != s[i]) j = next[j];
            if (s[j+1] == s[i]) j += 1;
            next[i] = j;
        }
		//以上实现next数组的预计算

        return s.substr(0, next[n - 1] + 1);  //直接截取即可，注意next存的是索引。
    }
};

代码提交结果：

3. Leetcode 214: 最短回文串

题目链接

解题思路: 首先将s反转后添加到s的前面，一定能满足题目要求。然后其实没必要讲反转后的s都添加到前面，例如$s="aabc"$, 那么前两个字符$"aa"$是没有必要参与反转添加的。即只要加上$"bc"$的反转变为$cbaabc$即可。

所以当s的某个前缀本身就是回文串的时候，没有必要再添加。

所以题目本质就是在求一个字符串的最长回文前缀。

接下来考虑如何求一个字符串的最长回文前缀。首先可以用暴力算法，遍历所有前缀，看其是否是回文串。

然后还可以参考KMP算法的思想。要判断一个字符串是回文串，即$s=s的反转$， 记作$s=s^{\prime }$。可以将s反转后加一个特殊字符添加到s的后面，构成一个新的字符串$s1=s{+}^{\prime }{\#}^{\prime }+s^{\prime }$，

例如初始$s="aabc"$, 那么$s1="aabc\#cbaa"$， 对s1求KMP算法中的next数组，假设求得的结果$j=next[n-1],(n=s1.size())$, 那么根据$next$数组的定义一定有$s1[0:j]=s1[(n-1-j):(n-1)]$。

而根据构造过程 s1 的后缀$s1[(n-1-j):(n-1)]$本身就是 s 的前缀$s[0:j]$的反转，所以可以得出s的前缀$s[0:j]=s[0:j]的反转$， 即$s[0:j]$就是找到的最长回文串。

class Solution {
public:
    void getNext(string s, vector<int> &next) {
        int n = s.size(), j = -1;
        next[0] = -1;
        for (int i = 1; i < n; i++) {
            while (j !=-1 && s[j + 1] != s[i]) j = next[j];
            if (s[j + 1] == s[i]) j += 1;
            next[i] = j;
        }
        return;
    }
    string shortestPalindrome(string s) {
        string rev_s = s;
        reverse(rev_s.begin(), rev_s.end());
        rev_s = s + '#' + rev_s; //s1的构造

        int m = rev_s.size();
        vector<int> next(m);
        getNext(rev_s, next); //KMP 算法中求next数组
        rev_s = s.substr(next[m - 1] + 1, s.size());  //s去掉了最长回文前缀
        reverse(rev_s.begin(), rev_s.end()); //反转后加到s的前面即可
        return rev_s + s;
    }
};

总结：利用KMP算法巧求字符串的最长回文前缀。
代码提交结果：

4. Leetcode 5: 最长回文子串(马拉车算法)

题目链接

题目解析：通过本题顺便介绍一种专门处理回文串的算法–马拉车算法(Manacher算法)。

马拉车算法的目的就是寻找字符串的最长回文子串。

马拉车算法首先将原字符串每个字符的前后分别加上一个特殊字符，比如原字符串为$"cbbd"$， 那么经过处理后的字符串变为$"\#c\#b\#b\#d\#"$。通过这种处理可以使字符串的长度变为奇数($n\to 2\cdot n+1$)，并且最长的回文子串也一定是奇数长度，即回文子串都可以以某一个字符为中心向左右扩展得到。

然后对扩充后的字符串 $s$ 的每个位置，定义一个回文半径数组$d[i]$，表示 $s$ 的$(i-d[i]:i+d[i])$ 部分的子串可以构成一个回文串。

然后从 $i=0\to 2\cdot n+1$ 依次计算每个位置的回文子串的半径。

$i=0$时很明显$d[i]=1$。因为以0位置的字符为中心，回文串只能是其本身。

假设 $d[0]\to d[i-1]$ 已经全都计算好，考虑如何计算$d[i]$。

因为 $i$ 位置可能包含在在之前计算过的某个回文串$(k-d[k],k+d[k])$之内，例如：

这种情况下$d[i]$可以直接等于$i$的对称点$j$对应的回文半径等于$d[j]$。因为$i$为中心的回文子串和$j$为中心的对应的回文子串是完全一样的。但前提是$i+d[i]$一定要小于$r$，否则还是要用朴素的比较方法依次比较$i$两边的字符是否相等。

具体可以参考如下的代码实现:

class Solution {
public:
    string getNewstring(string s) {
        string new_s;
        new_s += '#';
        for (int i = 0; s[i]; i++) {
            (new_s += s[i]) += '#';
        }
        return new_s;
    }
    string longestPalindrome(string s) {
        string new_s = getNewstring(s); //将s的每个字符前后分别加上特殊字符#
        int n = new_s.size(); 
        int l = 0, r = -1; //r表示之前回文串最右边的位置(不包含r)，l为r的对称点
        vector<int> d(n);
        for (int i = 0; i < n; i++) {
            if (i >= r) {
                d[i] = 1; //i >=r 表示i在之前的最远回文串之外
            }else {
                d[i] = min(r - i, d[l + r - i]); //l+r-i为i的对称点，d[i]不能超过r-i
            }
            //朴素依次比较
            while (i - d[i] >= 0 && i + d[i] <= n && new_s[i - d[i]] == new_s[i + d[i]] ) {
                d[i] += 1;
            }
            if (i + d[i] > r) {
                l = i - d[i]; 
                r = i + d[i];
            }
        }
        string ret;
        int tmp = 0; //最长回文子串的索引
        for (int i = 0; i < n; i++) {
            if (d[i] <= d[tmp]) continue;
            tmp = i; //更新tmp
        }
        //从（tmp-d[tmp], tmp+d[tmp]）位置还原最长回文子串
        for (int i = tmp - d[tmp] + 1; i < tmp + d[tmp]; i++) {
            if (i < 0 || i >= n) continue;
            if (new_s[i] == '#') continue;
            ret += new_s[i];
        }
        return ret;
    }
};

代码提交结果：

总结：马拉车算法思想较为简单，但是代码细节需多注意。

5. Leetcode 28: 找出字符串中第一个匹配项的下标

题目链接

解题思路：字符串匹配的经典问题，这里用之前讲过的Sunday算法实现。

class Solution {
public:
    int strStr(string haystack, string needle) {
        #define BASE 256
        int last_pos[BASE];
        int m;
        for (int i = 0; i < BASE; i++) last_pos[i] = -1;
        for (m = 0; needle[m]; m++) last_pos[needle[m]] = m;
        for (int i = 0; i + m <= haystack.size(); i += (m - last_pos[haystack[i + m]])) {
            int flag = 1;
            for (int j = 0; j < m; j++) {
                if (haystack[i + j] == needle[j]) continue;
                flag = 0;
                break;
            }
            if (flag) return i;
        }
        return -1;
    }
};

代码提交结果：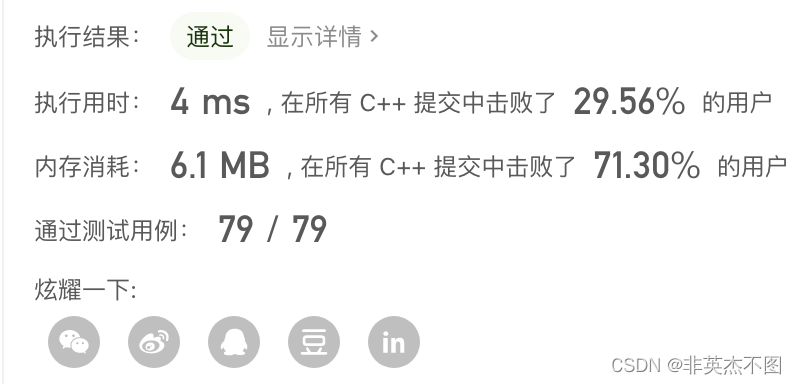

6. Leetcode 3: 无重复字符的最长子串

题目链接

题目解析：考虑字符$"abcabcbb"$，可以用不同长度的窗口取滑动该字符串，当窗口长度为0,1,2,3时，都可以存在一个窗口位置使得窗口内没有重复的字符串，当窗口长度超过3时，窗口内总会存在重复的字符。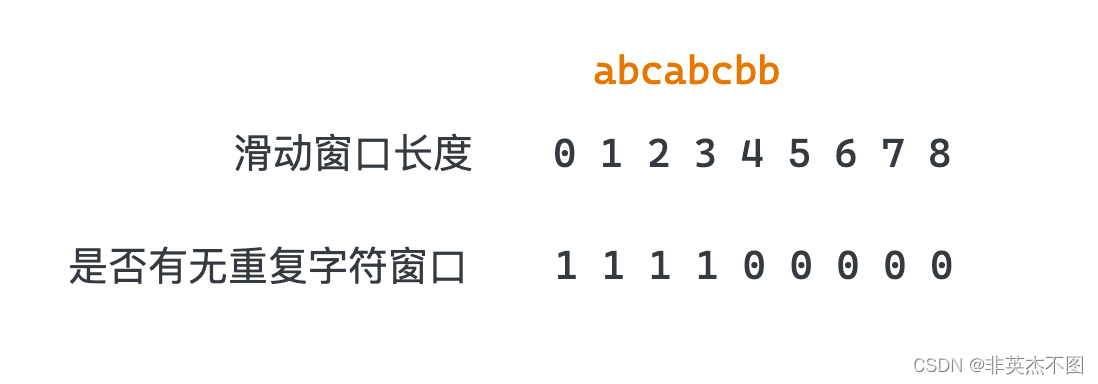

所以问题可以转化为前面一堆1，后面一堆0，寻找最后一个1的位置，即二分搜索问题。

然后需要考虑给定字符串和滑动窗口的长度，如何判断是否存在无重复字符的窗口位置。可以记录滑动窗口内无重复字符的个数，当其等于给定长度，则存在。

class Solution {
public:
    bool check(string s, int len) {
		//给定字符串和窗口长度len,判断是否存在无重复字符的窗口
        int cnt[256] = {0}; //字符和字符个数的映射关系
        int k = 0, n = s.size(); //k为窗口内无重复字符的个数
        for (int i = 0; i < n; i++) {
            if (cnt[s[i]] <= 0) k++;  //s[i]之前没有出现过，k才加一
            cnt[s[i]]++;
            if (i >= len) { 
                cnt[s[i - len]]--;
                if (cnt[s[i - len]] == 0) k--; //去掉最左边元素，k也可能要减一。
            }
            if (k == len) return true;

        }
        return false;
    }
    int lengthOfLongestSubstring(string s) {
        int n = s.size();
        if (n <= 1) return n;
        int l = 0, r = n, mid;

		//以下为二分搜索，前面一堆1，后面一堆0，寻找最后一个1
        while (l < r) {
            mid = (l + r + 1) / 2;
            if (check(s, mid)) l = mid;
            else r = mid - 1;
        }
        return l;
    }
};

提交结果：

总结：二分搜索写法固定，对于判断是否存在无重复字符的窗口，可以想的简单一点，直接维护窗口内无重复字符的个数。

7. Leetcode 14: 最长公共前缀

题目链接

题目解析：没有学过字典树的情况下可以考虑暴力比较。即先找到前两个字符的最长公共前缀，在找到这个前缀和第三个字符的最长公共前缀，如此一直找下去。

class Solution {
public:
    string compare(string &a, string &b) {
    	//寻找两个字符串的最长公共前缀
        string ret = "";
        for (int i = 0; a[i]; i++) {
            if (i >= b.size() || a[i] != b[i]) break;
            ret += a[i];
        }
        return ret;
    }
    string longestCommonPrefix(vector<string>& strs) {
        string ret = strs[0];
        for (int i = 1; i < strs.size(); i++) {
            ret = compare(ret, strs[i]);
        }
        return ret;
    }
};

代码提交结果：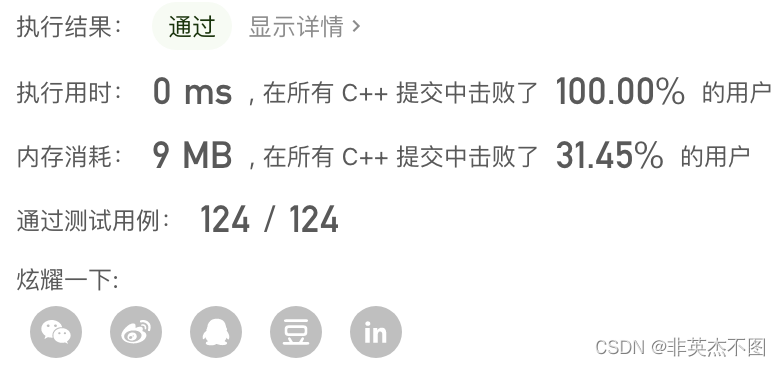

8. 面试题01.05: 一次编辑

题目链接

题目解析：可以分类讨论。首先如果两个字符串的长度之差大于1，则肯定不能通过一次编辑得到；

如果两个字符串的长度相等，则可以依次比较每一位，记录不相等的字符个数；

如果两个字符串的长度相差为1，则依次比较每一位，遇到不相等的位置时，较长的那个字符索引+1，否则两个字符串的索引都+1，同样记录不相等的字符个数。

class Solution {
public:
    bool oneEditAway(string first, string second) {
        if (first.size() < second.size()) swap(first, second); //保证first一定是更长的
        int n = first.size(), m = second.size();
        if (n - m >= 2) return false;
        if (n == m) {
            int diff_num = 0;
            for (int i = 0; first[i]; i++) { //依次比较每一位；
                if (first[i] ==second[i] ) continue;
                diff_num++;
                if (diff_num >= 2) return false;
            }
            return true;
        }
        int i, j, diff_num = 0;
        for (i = 0, j = 0; i < n, j < m;) {
            if (first[i] == second[j]) {
                i++, j++; //依次比较每一位
                continue;
            }
            diff_num++; //遇到不相等的位置时只有i+1
            if (diff_num >= 2) return false;
            i++;
        }
        return true;
    }
};

提交结果：

9. Leetcode 12: 整数转罗马数字

题目链接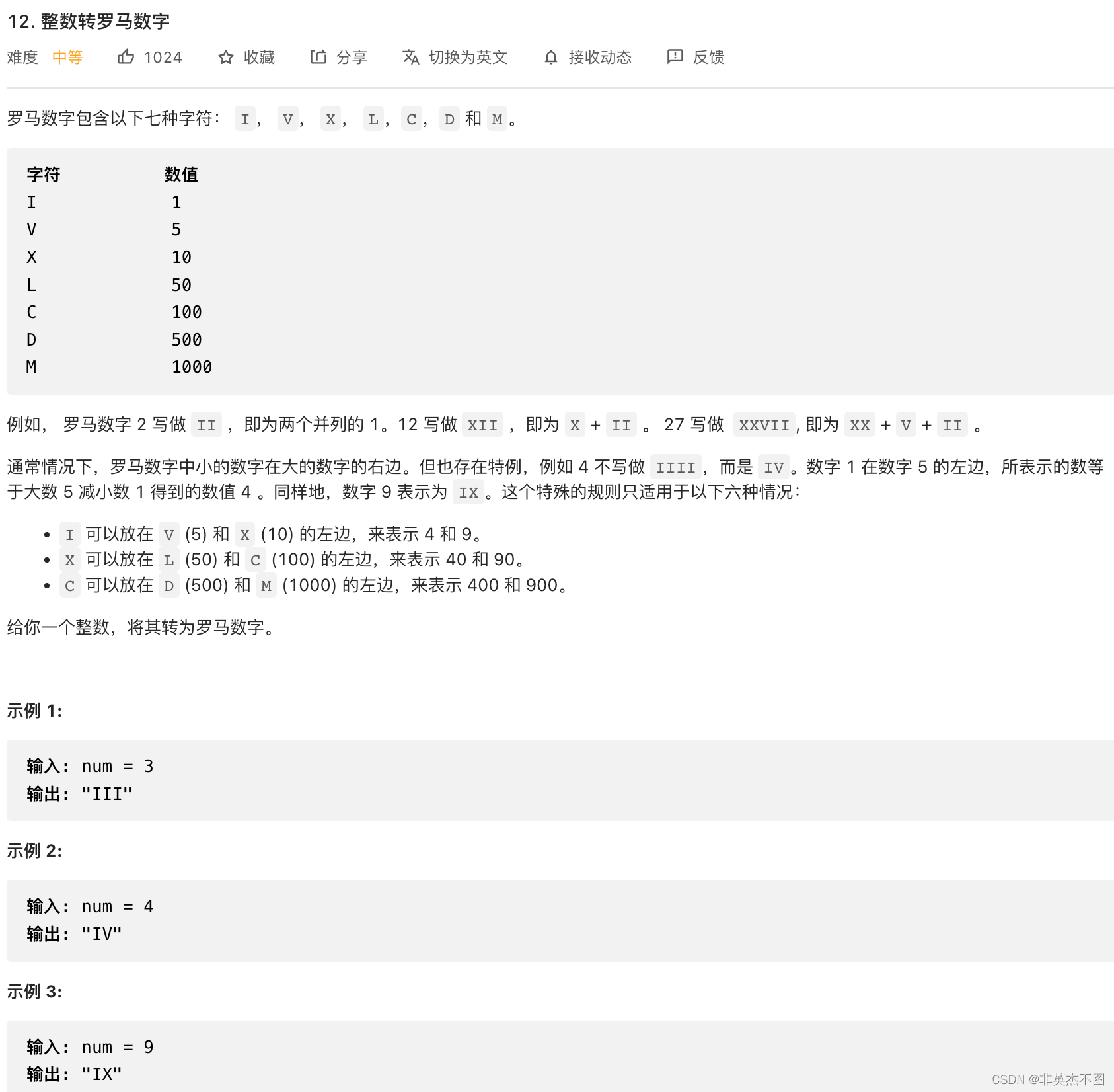

题目解析：可以将数字分为大于1000， 100-1000， 10-100， 0-10几类。

例如假设数字在100-1000，有d个100，则可以根据d的具体数值分类讨论，输出结果字符串的值。

d == 4: 输出 CD；

d == 9: 输出 CM;

d >= 5: 输出 D， 然后让d -= 5;

最后输出d个C。

class Solution {
public:
    string RomanString(int d, char a, char b, char c) {
        string ret = "";
        // printf("d : %d, %c %c %c \n", d, a, b, c);
        if (d == 4 || d == 9) {
            ret += a;
            ret += (d == 4 ? b : c);
            return ret;
        }
        if (d >= 5) {ret += b; d -= 5;}
        
        while (d > 0) {
            ret += a;
            d--;
        }
        return ret;
    }
    string output(int &num) {
        if (num >= 1000) {
            int d = num / 1000; //有几个1000
            num = num % 1000;
            return RomanString(d, 'M', 'M', 'M'); // 数值范围最多有3个1000
        }else if (num >= 100) {
            int d = num / 100; //有几个100
            num = num % 100;
            return RomanString(d, 'C', 'D', 'M');
        }else if (num >= 10) {
            int d = num / 10;
            num = num % 10;
            return RomanString(d, 'X', 'L', 'C');
        }else{
            int d = num;
            num = 0;
            return RomanString(d, 'I', 'V', 'X');
        }
        return "";
    }
    string intToRoman(int num) {
        string ret;
        while (num) {
            // printf("num : %d\n", num);
            ret += output(num);
        }
        return ret;
    }
};

代码提交结果：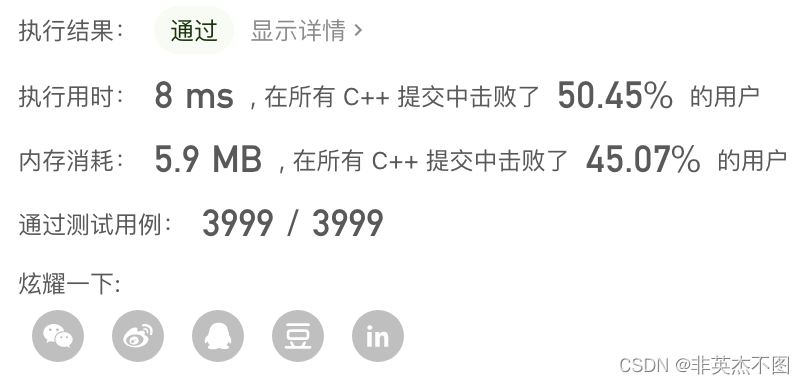

总结：代码模拟，但是模拟的过程中有技巧和总结。