神经网络中激活函数的比较

1，Sigmoid

数学公式：

sigmoid非线性函数的数学公式及图象是

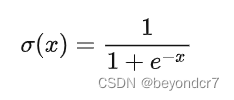
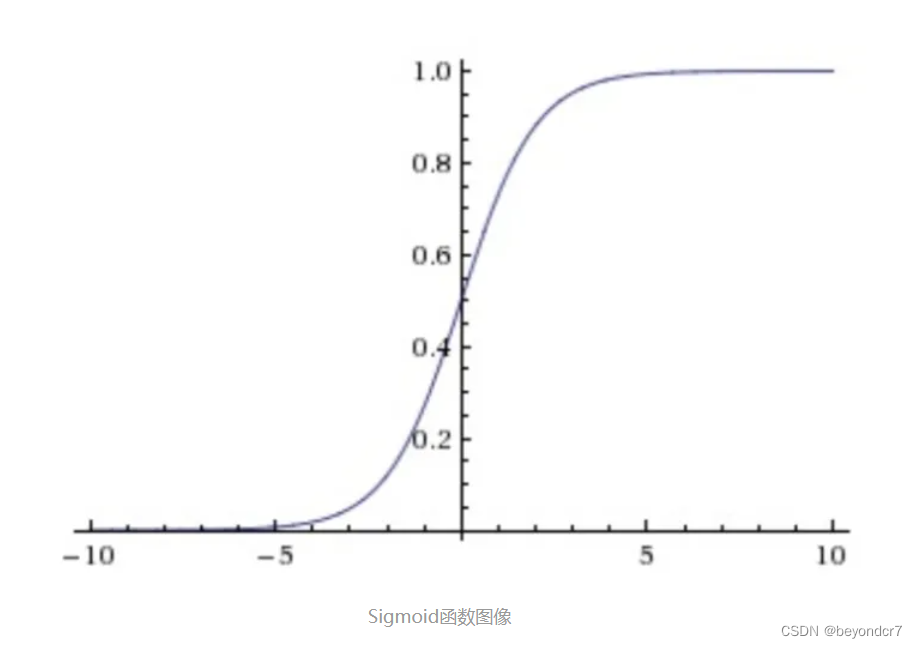
它输入实数值并将其“挤压”到0到1范围内，适合输出为概率的情况；

存在问题：

• Sigmoid函数饱和使梯度消失。当神经元的激活在接近0或1处时会饱和，在这些区域梯度几乎为0，这就会导致梯度消失，几乎就有没有信号通过神经传回上一层。
• Sigmoid函数的输出不是零中心的。因为如果输入神经元的数据总是正数，那么关于�的梯度在反向传播的过程中，将会要么全部是正数，要么全部是负数，这将会导致梯度下降权重更新时出现z字型的下降。

2，Tanh

数学公式：

Tanh非线性函数的数学公式及图象是

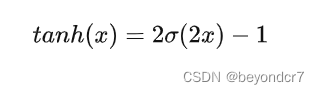
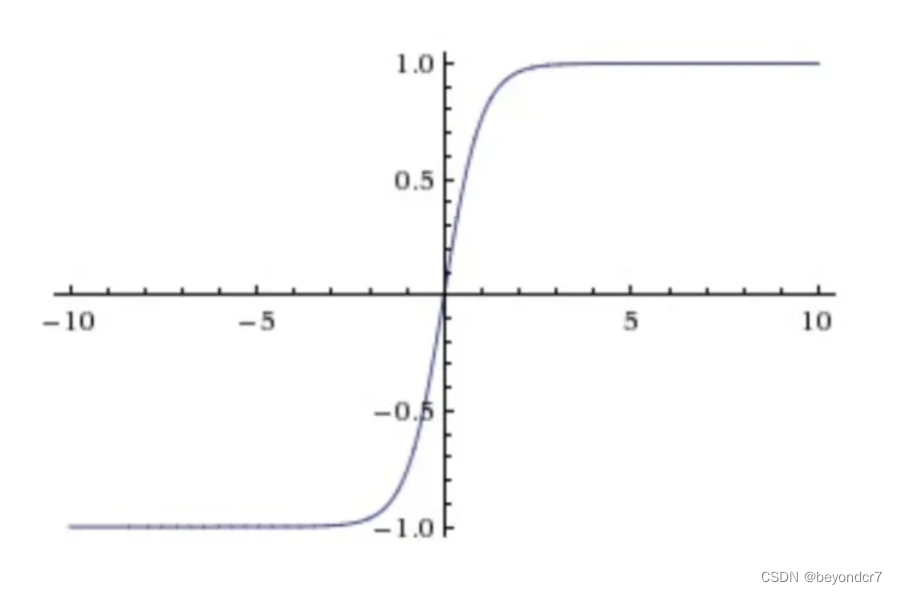
Tanh非线性函数将实数值压缩到[-1,1]之间；

存在问题：

Tanh解决了Sigmoid的输出是不是零中心的问题，但仍然存在饱和问题。

3，ReLU

数学公式：

函数公式及图象是

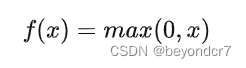
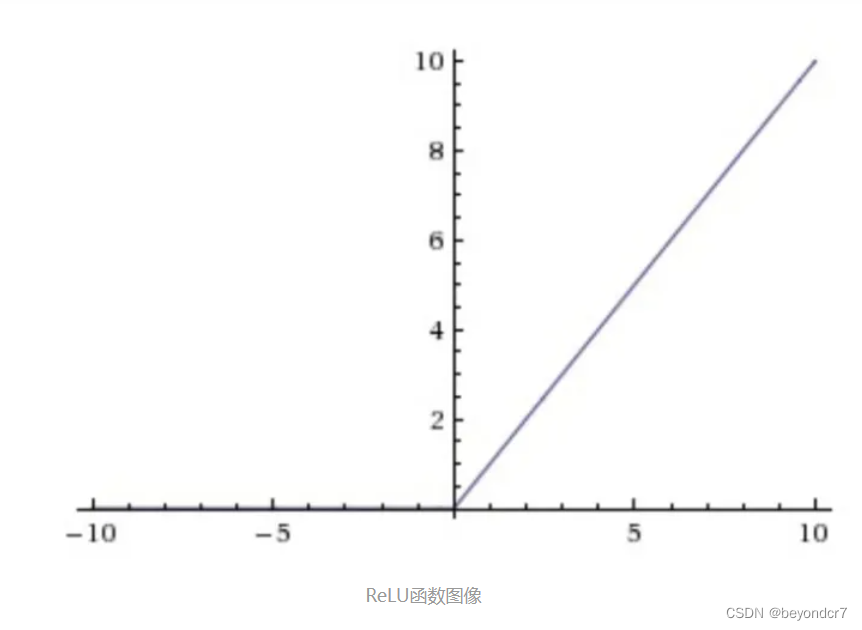
相较于sigmoid和tanh函数，ReLU对于随机梯度下降的收敛有巨大的加速作用；sigmoid和tanh在求导时含有指数运算，而ReLU求导几乎不存在任何计算量。

对比sigmoid类函数主要变化是：

1）单侧抑制；

2）相对宽阔的兴奋边界；

3）稀疏激活性。

存在问题：

ReLU单元比较脆弱并且可能“死掉”，而且是不可逆的，因此导致了数据多样化的丢失。通过合理设置学习率，会降低神经元死亡的概率。

4，Leaky ReLU

数学公式：

函数公式是

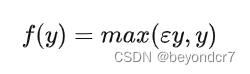
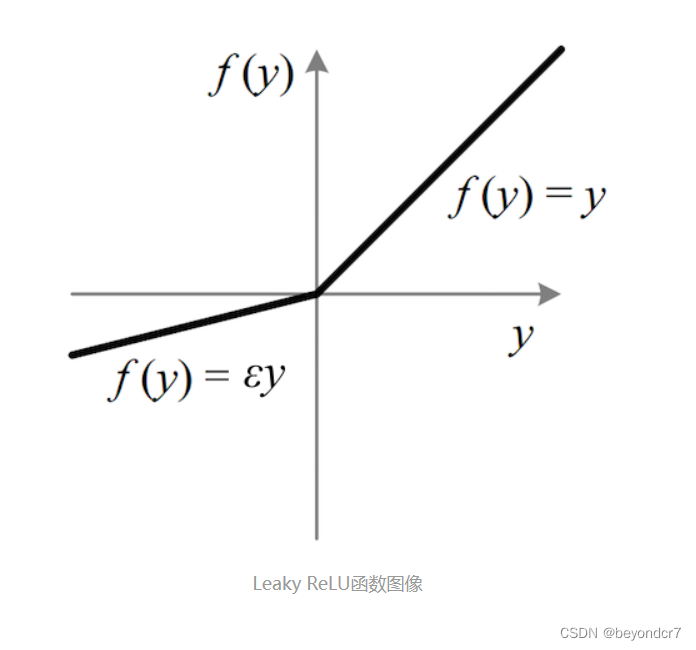
其中ε 是很小的负数梯度值，比如0.01。这样做目的是使负轴信息不会全部丢失，解决了ReLU神经元“死掉”的问题。更进一步的方法是PReLU，即把 ε当做每个神经元中的一个参数，是可以通过梯度下降求解的。

 5，

Softmax

数学公式：

Softmax用于多分类神经网络输出，目的是让大的更大。函数公式是

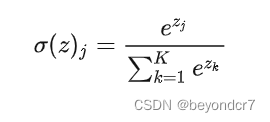
示意图如下。

Softmax示意图

Softmax是Sigmoid的扩展，当类别数k＝2时，Softmax回归退化为Logistic回归。