从该公众号的第一篇文章到现在，刚刚过去一整年，决定给自己开个大坑，说一下CT的重建算法。
今天这篇字数偏多，但理解难度不大，希望对大家有所帮助。
CT图像重建的数学原理对于影像技术专业的同学来说过于晦涩难懂，我的数学很渣，看不懂那些数学公式和微分计算，不过也不影响学习基础的原理知识，此次不涉及复杂的数学计算和公式，尽量用浅显易懂的语言来聊一聊几种常见和经典的图像重建方法的原理，由于重建的方法很多，一篇讲完篇幅过长，我会分好几部分来发。
CT技术是在不断的进步和发展中的，所以重建方法也是在不断的进步中，不同的重建方法有不同的时代性；
早期的CT发出的X线是笔形束，第二代CT以后为扇形束，而螺旋CT发展起来以后为锥形束；
针对笔形束、扇形束和锥形束分别有不同的算法，但是各种算法的基础理论还是依靠笔形束的几种经典算法借鉴、发展和改进而来。
先来总览一下CT图像重建的常见算法：
一、
第一代CT发出的射线为笔形束，属于平行线束，经典的算法有三种：
1.傅立叶变换法
(FT：Fourier Transform)
2.滤波反投影法
(FBP：Filtered back-projection)
3.迭代法
(IR：Iterative Reconstruction)
二、
第二代至第五代CT发出的射线均为扇形束，每个线束之间有夹角，算法主要是先将扇形束转换为平行束，再进行平行束算法进行重建；
三、
螺旋CT的锥形束算法最为复杂，主要是基于FDK算法，这个是精确锥形束重建算法的基础，而FDK算法又可以看成是二维经典FBP(滤波反投影)算法依据锥角的大小来近似的一种算法，大家也不用去管FDK算法具体是什么，只需要知道基于滤波反投影算法即可。
这么多算法其实追根溯源还是那几种平行线束的算法，所以就重点说一下FT、FBP、IR这三种算法。
今天就重点说一下：
FT(傅立叶变换)算法
傅立叶变换是一个复杂但是相当实用的工具，应用领域相当广泛；
这个算法属于解析法的范畴，成像过程是需要列一堆公式去进行大量数学计算才能得到结果；
傅立叶变换想要几句话解释清楚是不可能的，简单概述一下就是：
将时域非周期连续信号转换为频域非周期连续信号
感兴趣的可以看下这个链接：
https://www.cnblogs.com/h2zZhou/p/8405717.html
咱们今天不讲傅立叶变换的具体过程，而是说一下如何通过傅立叶变换得到图像。
傅立叶变换重建法有一个定理需要理解
中心切片定理：
一个三维(二维)物体的二维(一维)投影的傅立叶变换精确的等于物体的傅立叶变换的中心截面
如何去理解？看一幅图：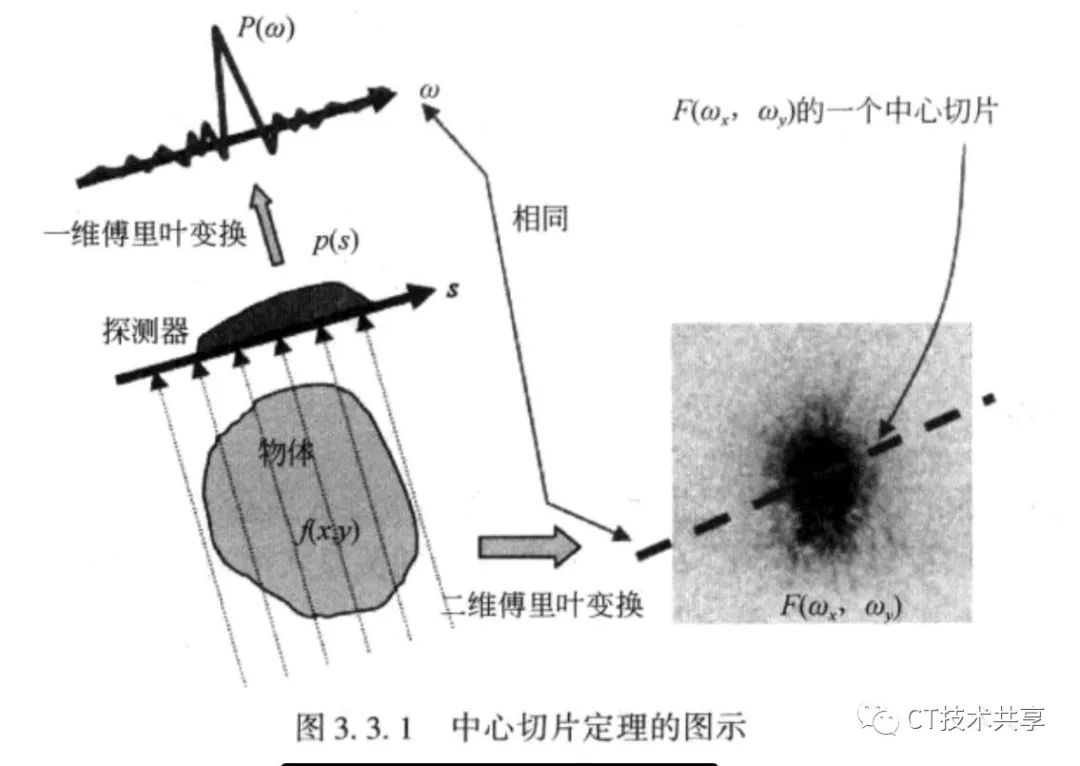
图片来源：CT原理与技术 主编：余晓锷 龚剑
咱们拆分开那句定理，逐字逐句来看：
1.一个三维(二维)物体的二维(一维)投影
2.的傅立叶变换
3.精确的等于
4.物体的傅立叶变换
5.的中心截面
废话不多说，上图：
第一句：
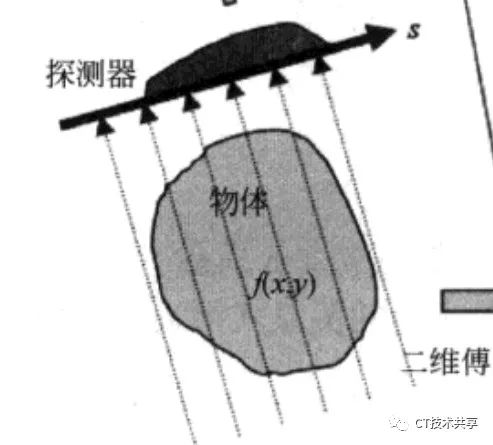
探测器采集到的物体某个方向的投影数据
第二句：
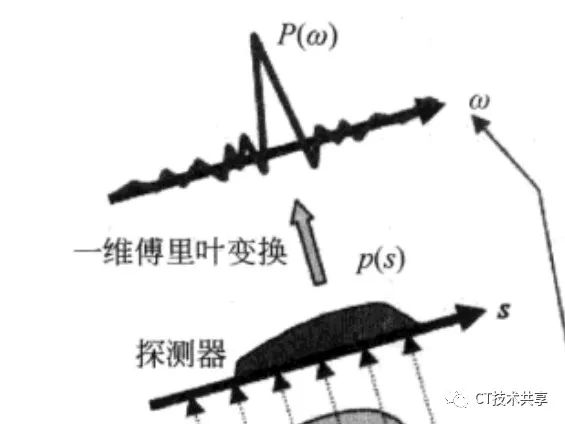
投影数据经过傅立叶变换，变成了频域数据
第三句先不说
第四句：
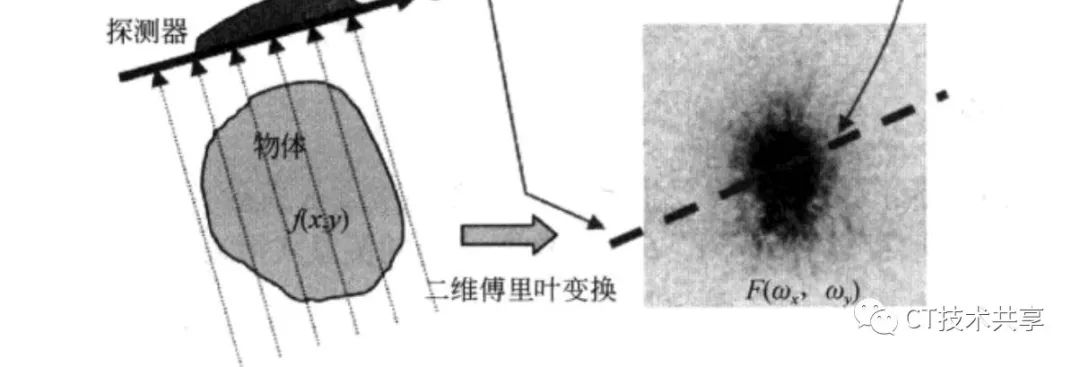
这是指物体整体的傅立叶变换，而不是指单纯的一个投影了，变换后的数据就是这样：
为什么是这样呢？我当时迷惑了很久也搞不清楚，后来我大概了解了傅立叶变换的过程后就明白是咋回事了
给大家看一个傅立叶变换的结果
这是一个矩形图形
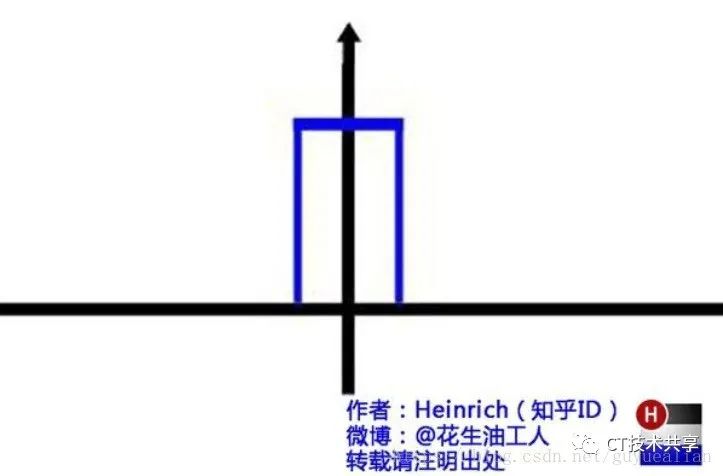
经过傅立叶变换后，是这样的：
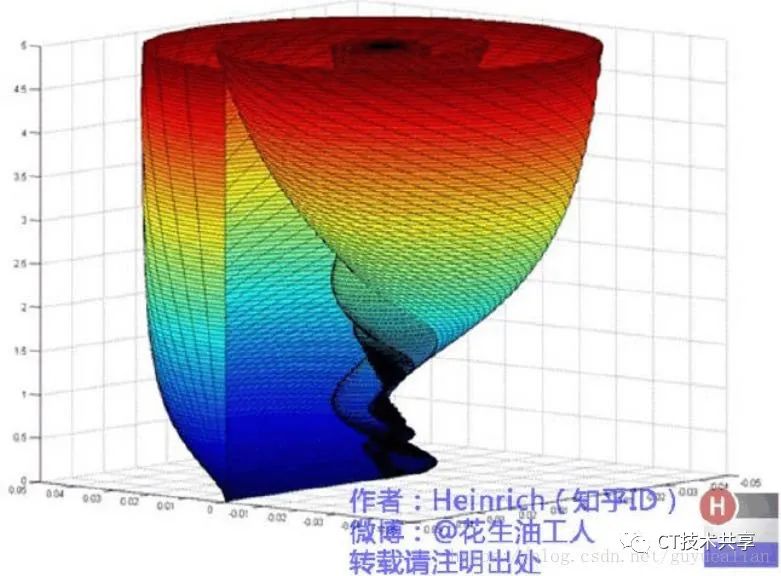
上图来源：https://blog.csdn.net/guyuealian/article/details/72817527
可以看到，一个简单的矩形，经过傅立叶变换后成了一个类似海螺一样的螺旋体
而这幅图如果从上往下看的话，岂不是和之前物体傅立叶变换之后的图非常相似？
所以可以理解为这个图代表傅立叶变换后的数据
第五句：
傅立叶变换后的数据等价于上面那副螺旋上升状彩图；
但其实那幅图是振幅、频率加相位后在复数域的后处理融合图；
如果对这个数据进行截面处理(必须要经过中心，所以才叫中心截面，就和上图的红圈内的那条线一样)；
那么就能得到这个频域数据的截面数据，
这个截面数据同样也是频域数据。
此时再回到第三句：
精确的等于
意思就是：
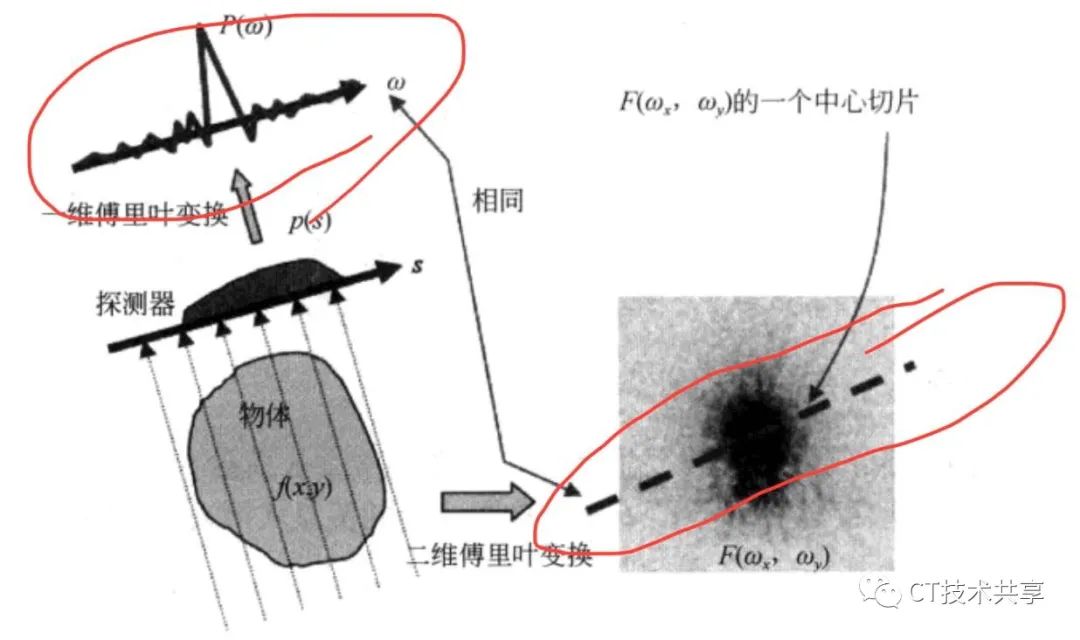
这两个红圈内的数据相等。
这个定理经过逐句分析，应该不难理解，接下来就是由这个定理推出来的如何进行图像重建的方法了：
假设有一个物体的某个断层数据需要重建；
首先收集此断层的各个方向的投影数据；
然后对这些投影数据进行傅立叶变换；
得到变换后的投影频域数据；
把诸多投影数据组合就能构成物体完整的傅立叶变换数据；
然后把完整的数据进行反傅立叶变换；
就能得到此断层重建图像。
投影数据就是X射线穿透物体后的衰减信息
而这个算法的关键就是需要采集各个方向的投影数据
第一代CT的扫描方式是笔形束加平移加旋转的扫描方法，就是一个窄射线束对着人体进行平移扫描，扫描完这个角度后机架整体旋转一度进行下一个角度的平移扫描，一直旋转180度，得到180个断层数据，然后再进行重建，而由于射线束很窄，又是平移扫描，所以可以看成是平行线束。
在CT发展的早期，此算法被广泛使用
但是此算法有数个缺点，导致后来应用越来越少：
1、高频信号有所失真，解剖细节显示不佳
2、运算量大，占用内存大，早期计算机性能不佳，导致成像时间过长
3、采集数据多，无法进行快速扫描
4、难以完成目标重建(靶重建)
如果觉得此篇文章有所帮助，可以扫码关注此公众号，不定期更新一些CT技术原理方面的见解，不足之处欢迎批评指正，感谢支持！
