1. 单值二叉树。
用根的值与左右字树的值进行判断; 看是否都相等
class Solution {
public:
bool isU(struct TreeNode* root, int key){
if (root == NULL)
return true;
return root->val == key
&& isU(root->left, key)
&& isU(root->right, key);
}
bool isUnivalTree(struct TreeNode* root){
return isU(root, root->val);
}
};
2. 二叉树最大深度
思路:依次得到左右两边的深度;然后比较左右深度的大小, 大的那一边就是二叉树的深度
int maxDepth(struct TreeNode* root){
if (root == NULL)
return 0;
//依次得到左右两边的深度
int leftDepth = maxDepth(root->left) + 1;
int rightDepth = maxDepth(root->right) + 1;
return leftDepth > rightDepth ? leftDepth : rightDepth;
}
//C++
public class TreeDepth {
//取得二叉树的最大深度
public int maxDepth(TreeNode root){
if (root == null){
return 0;
}
return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
}
//取得二叉树的最小深度
public int minDepth(TreeNode root) {
if (root == null){
return 0;
}
if (root.left == null){
return minDepth(root.right) + 1;
}
if (root.right == null){
return minDepth(root.left) + 1;
}
return Math.min(minDepth(root.left), minDepth(root.right)) + 1;
}
}
3. 翻转二叉树。
class Solution {
public:
//执行翻转的过程
void _invertT(TreeNode* root) {
if (root) {
//翻转当前节点的左右孩子节点
TreeNode* tmp = root->left;
root->left = root->right;
root->right = tmp; \
//递归翻转当前左右节点的孩子节点
_invertT(root->left);
_invertT(root->right);
}
}
TreeNode* invertTree(TreeNode* root) {
_invertT(root);
return root;
}
};
4. 检查两颗树是否相同。
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
//两个同时为空
if (p == NULL && q == NULL)
return true;
//一个为空;一个不为空
if (p == NULL || q == NULL)
return false;
//判断当前节点是否相等,
return p->val == q->val
//判断左子树是否相等
&& isSameTree(p->left, q->left)
//判断右子树是否相等
&& isSameTree(p->right, q->right);
}
//C++
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
if (p == NULL && q == NULL)
return true;
if (p == NULL || q == NULL)
return false;
return p->val == q->val
&& isSameTree(p->left, q->left)
&& isSameTree(p->right, q->right);
}
};
5. 对称二叉树。OJ链接
class Solution {
public:
bool isS(TreeNode* p, TreeNode* q) {
if (p == NULL && q == NULL)
return true;
if (p == NULL || q == NULL)
return false;
return p->val == q->val
&& isS(p->left, q->right)
&& isS(p->right, q->left);
}
bool isSymmetric(TreeNode* root) {
if (root == NULL)
return true;
return isS(root->left, root->right);
}
};
6. 二叉树的前序遍历。
//求树的节点个数
int getSize(struct TreeNode* root) {
if (root == NULL)
return 0;
return getSize(root->left) + getSize(root->right) + 1;
}
//前序遍历
void _preorderT(struct TreeNode* root, int* array, int* idx) {
if (root) {
array[*idx] = root->val;
(*idx)++;
_preorderT(root->left, array, idx);
_preorderT(root->right, array, idx);
}
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){
int* array = (int*)malloc(sizeof(int)*getSize(root));
//遍历,保存节点
*returnSize = 0;
_preorderT(root, array, returnSize);
return array;
}
//C++
class Solution {
public:
//前序遍历
void _preorderT(TreeNode* root, vector<int>& array) {
if (root) {
array.push_back(root->val);
_preorderT(root->left, array);
_preorderT(root->right, array);
}
}
vector<int> preorderTraversal(TreeNode* root) {
vector<int> array;
_preorderT(root, array);
return array;
}
};
7. 二叉树中序遍历 。
//二叉树节点的个数
int getSize(struct TreeNode* root) {
if (root == NULL)
return 0;
return getSize(root->left) + getSize(root->right) + 1;
}
void _inorderT(struct TreeNode* root, int* array, int* idx){
if (root) {
_inorderT(root->left, array, idx);
array[*idx] = root->val;
(*idx)++;
_inorderT(root->right, array, idx);
}
}
int* inorderTraversal(struct TreeNode* root, int* returnSize){
//申请数组空间
int* array = (int*)malloc(sizeof(int)*getSize(root));
// 中序遍历 依次将二叉树节点元素存放到数组中
*returnSize = 0;
_inorderT(root, array, returnSize);
return array;
}
//C++
class Solution {
public:
void _inorderT(TreeNode* root, vector<int>& array) {
if (root) {
_inorderT(root->left, array);
array.push_back(root->val);
_inorderT(root->right, array);
}
}
vector<int> inorderTraversal(TreeNode* root) {
vector<int> array;
_inorderT(root, array);
return array;
}
};
8. 二叉树的后序遍历 。
//二叉树节点个数
int getSize(struct TreeNode* root) {
if (root == NULL)
return 0;
return getSize(root->left) + getSize(root->right) + 1;
}
//后序遍历
void _postorderT(struct TreeNode* root, int* array, int* idx) {
if (root) {
_postorderT(root->left, array, idx);
_postorderT(root->right, array, idx);
array[*idx] = root->val;
(*idx)++;
}
}
int* postorderTraversal(struct TreeNode* root, int* returnSize){
int* array = (int*)malloc(sizeof(int)*getSize(root));
*returnSize = 0;
_postorderT(root, array, returnSize);
return array;
}
//C++
class Solution {
public:
void _postorderT(TreeNode* root, vector<int>& array) {
if (root) {
_postorderT(root->left, array);
_postorderT(root->right, array);
array.push_back(root->val);
}
}
vector<int> postorderTraversal(TreeNode* root) {
vector<int> array;
_postorderT(root, array);
return array;
}
};
9. 另一颗树的子树。
class Solution {
public:
//解题思路
//1.两个二叉树整体是否相同
//2.左子树是否和另一个二叉树相同
//3.右子树是否和另一个二叉树相同
//判定两个二叉树是否相同的代码
bool isSame(TreeNode* p, TreeNode* q) {
if (p == NULL && q == NULL)
return true;
if (p == NULL || q == NULL)
return false;
return p->val == q->val
&& isSame(p->left, q->left)
&& isSame(p->right, q->right);
}
bool isSubtree(TreeNode* root, TreeNode* subRoot) {
if (subRoot == NULL)
return true;
if (root == NULL)
return false;
//1.两个二叉树整体是否相同
return isSame(root, subRoot)
//2.左子树是否和另一个二叉树相同
|| isSubtree(root->left, subRoot)
|| isSubtree(root->right, subRoot);
}
};
10. 判断一颗二叉树是否是平衡二叉树。
class Solution {
public:
int getDeth(TreeNode* root) {
if (root == NULL)
return 0;
int left = getDeth(root->left) + 1;
int right = getDeth(root->right) + 1;
return left > right ? left : right;
}
bool isBalanced(TreeNode* root) {
if (root == NULL)
return true;
int l = getDeth(root->left);
int r = getDeth(root->right);
//因为判定的是每一个节点, 因此根节点判断是否平衡之后, 还要判断以左/右孩子为根节点时,依次递归进行判断
return abs(l - r) < 2
&& isBalanced(root->left)
&& isBalanced(root->right);
}
};
11. 二叉树的构建及遍历。
二叉树的构建: 使用数组进行递归构建 遍历: 中序遍历
#include <iostream>
#include <string>
using namespace std;
typedef struct Node{
Node* left;
Node* right;
char val;
//构造函数初始化
Node(char x)
:val(x)
, left(nullptr)
, right(nullptr)
{}
};
string s;
Node* creatTree(int& i) {
if (s[i] == '#')
return ;
Node* node = new Node(s[i]); //若不为'#',则创建该节点, 并为本节点赋值
//(i++);
node->left = creatTree(++i);//创建左节点
//(++i);
node->right = creatTree(++i);//创建右节点
return node;
}
//中序遍历节点
void inOrder(Node* root) {
if (root) {
inOrder(root->left);
cout << root->val << " ";
inOrder(root->right);
}
}
int main() {
while (cin >> s) {
int i = 0;
Node* root = creatTree(i);
inOrder(root);
cout << endl;
}
system("pause");
return 0;
}
实现二叉树的四种遍历方式
前序遍历 node left right abdec
中序遍历 left node right dbeac
后序遍历 left right node debca
层序遍历: 从第一层开始,每一层都进行遍历
#include <iostream>
#include <vector>
#include <stack>
#include <queue>
using namespace std;
struct Node{
int value;
Node* leftChild;
Node* rightChild;
};
class Solution {
public:
//前序遍历
//递归
void preorderTraversal(Node *root) {
if (root) {
cout<<root->value<<" ";
preorderTraversal(root->leftChild);
preorderTraversal(root->rightChild);
}
}
//非递归
void NopreorderTraversal(Node *root) {
if (root == nullptr)
return;
stack<Node*> st;
st.push(root);
while (!st.empty()) {
//得到栈顶元素: 直接打印
root = st.top();
st.pop();
cout << root->value << " ";
//右孩子存在, 右孩子直接压栈
if (root->rightChild)
st.push(root->rightChild);
//左孩子存在, 左孩子直接压栈
if (root->leftChild)
st.push(root->leftChild);
}
}
//中序遍历
//递归
void midOrderTraversal(Node *root) {
if (root) {
midOrderTraversal(root->leftChild);
cout << root->value << " ";
midOrderTraversal(root->rightChild);
}
}
//非递归
void NomidOrderTraversal(Node *root) {
if (root == nullptr)
return;
stack<Node*> st;
while (!st.empty() || root != nullptr) {
if (root != nullptr) {
st.push(root);
root = root->leftChild;
}
else {
root = st.top();
st.pop();
cout << root->value << " ";
root = root->rightChild;
}
}
}
//后序遍历
/*左儿子和右儿子都为空;
没有右儿子,左儿子从栈里弹出了;
有右儿子,右儿子从栈里弹出了。*/
//递归
void posOrderTraversal(Node *root) {
if (root) {
midOrderTraversal(root->leftChild);
midOrderTraversal(root->rightChild);
cout << root->value << " ";
}
}
//非递归
void NoposOrderTraversal(Node *root) {
if (root == nullptr)
return;
stack<Node*> st;
st.push(root);
stack<int> tmp;
while (!st.empty()) {
root = st.top();
st.pop();
tmp.push(root->value);
if (root->leftChild)
st.push(root->leftChild);
if (root->rightChild)
st.push(root->rightChild);
}
while (!tmp.empty()){
cout << tmp.top() << " ";
tmp.pop();
}
}
//层序遍历
void levelTraversal(Node *root) {
if (root == nullptr)
return;
queue<Node*> q;
q.push(root);
while (!q.empty()) {
root = q.front();
q.pop();
cout << root->value << " ";
if (root->leftChild)
q.push(root->leftChild);
if (root->rightChild)
q.push(root->rightChild);
}
}
};
int main() {
cout << "二叉树遍历的实现: 递归和非递归" << endl;
Node *root = new Node;
root->value = 1;
root->leftChild = new Node;
root->leftChild->value = 2;
root->rightChild = new Node;
root->rightChild->value = 3;
root->leftChild->leftChild = new Node;
root->leftChild->leftChild->value = 4;
root->leftChild->rightChild = new Node;
root->leftChild->rightChild->value = 5;
root->rightChild->leftChild = new Node;
root->rightChild->leftChild->value = 6;
root->leftChild->leftChild->leftChild = nullptr;
root->leftChild->leftChild->rightChild = nullptr;
root->leftChild->rightChild->leftChild = nullptr;
root->leftChild->rightChild->rightChild = nullptr;
root->rightChild->leftChild->leftChild = nullptr;
root->rightChild->leftChild->rightChild = nullptr;
root->rightChild->rightChild = nullptr;
Solution s;
cout << "前序遍历: (递归)" << endl;
s.preorderTraversal(root);
cout << "\n前序遍历: (非递归)" << endl;
s.NopreorderTraversal(root);
cout << "\n中序遍历: (递归)" << endl;
s.midOrderTraversal(root);
cout << "\n中序遍历: (非递归)" << endl;
s.NomidOrderTraversal(root);
cout << "\n后序遍历: (递归)" << endl;
s.posOrderTraversal(root);
cout << "\n后序遍历: (非递归)" << endl;
s.NoposOrderTraversal(root);
cout << "\n层序遍历: " << endl;
s.levelTraversal(root);
cout << "\n";
system("pause");
return 0;
}
运行结果: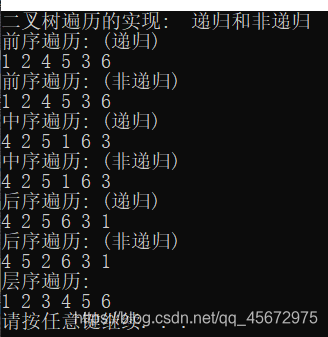
版权声明:本文为qq_45672975原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。