1 根轨迹与系统性能
(1)定义:指系统某一参数从零变化到无穷大时,闭环系统特征方程式的根(闭环极点)在s平面上变化的轨迹。
Matlab命令:rlocus(sys),默认变化参数为开环传递函数的增益k。
(2)功能:根轨迹可以直接给出闭环系统时间相应的全部信息,而且可以指明开环零、极点应该如何变化才能满足给定的闭环系统的性能指标要求。
根轨迹方法可以求解高阶代数方程的根,实际上就是解决闭环特征方程式的求根问题。
(3)根据:系统的稳定性由系统闭环极点唯一确定,而系统的稳态性能和动态性能与闭环零、极点在s平面上的位置密切相关。
(4)思想:由开环根轨迹,推出闭环系统性能。
从已知的开环零、极点分布,及根轨迹增益,通过图解的方法找到闭环极点。
这一方法不直接求解特征方程,用作图的方法表示特征方程的根与系统某一参数的全部数值关系,当这一参数取特定值时,对应的特征根可在上述关系图中找到。
(5)开环系统根轨迹增益、开环增益之间相差一个比例常数。
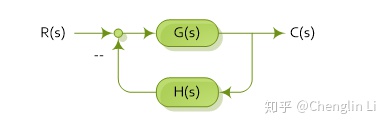


2 根轨迹方程
(1)说明:根轨迹是系统所有闭环极点的集合。

(2)应用相位条件找出所有可能的根轨迹,然后利用幅值条件在根轨迹上标出参数值。
3 绘制根轨迹
(1)根轨迹的分支数
根轨迹在
(2)根轨迹的连续性和对称性
参数 连续变化,特征方程的根连续变化、根轨迹具有连续性。
根轨迹是对称于实轴的连续曲线。
(3)根轨迹的起点和终点
- 对于单位反馈系统,闭环零点就是开环零点;
- 对于单位反馈系统,闭环系统根轨迹增益就是开环系统根轨迹增益;
根轨迹的起点终点分别是

(4)根轨迹的渐近线
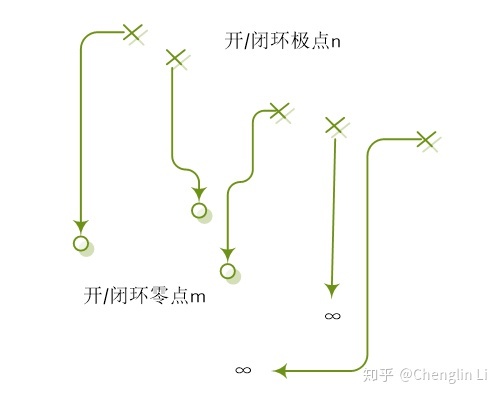

(5)实轴上的根轨迹
实轴上的某一区域,若其右边开环实数零、极点个数之和为奇数,则该区域必是根轨迹。共轭复数开环零、极点对确定实轴上的根轨迹无影响。

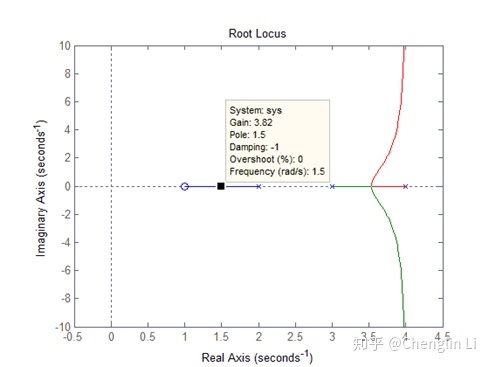
(6)根轨迹与实轴的交点

(7)根轨迹与虚轴的交点
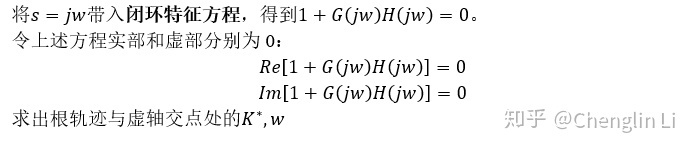
(8)根轨迹的出射角与入射角(不是复数无需计算)
出射角:离开开环复数极点处的切线方向,与实轴正方向之间的夹角。
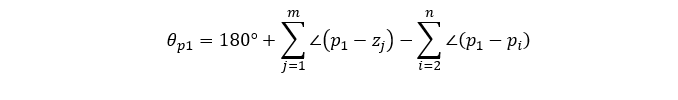
入射角:进入开环复数零点处的切线方向,与实轴正方向之间的夹角。
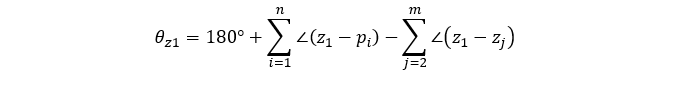
(9)闭环极点的和与积(韦达定理)
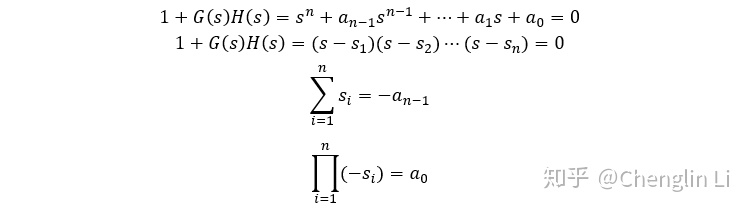
4 附加开环零点
(1)在
(2)可以使系统的根轨迹图,发生趋向于附加开环零点方向的变化,而且这种影响将随开环零点接近坐标原点的程序而加强。
5 主导极点
(1)系统动态性能由接近虚轴的闭环极点确定,对应的响应分量在系统响应中起主导作用,这样的极点,称为主导极点。
(2)闭环实数主导极点的作用,相当于增大系统的阻尼,使峰值时间滞后,超调量下降。
(3)其它极点与该极点的距离较远,且距离虚轴的距离也较该极点远,否则,无法区分主次。
(4)极点附近应没有零点,从数学表达式看极点在分母,零点在分子,正好是相反的作用,相距较近时数学上可抵消,工程中作用也相反。
(5)一个实际系统的主导极点可以是一个,两个或数个。这要视具体系统的具体情况。主导极点可以是实数,也可以是复数。
——2020.04.30——