几种常见的基于比较的排序方式
排序简介

这些排序都给了示例图,可能没有视频那么生动,但图片也有视频没有的好处,那就是读者可以仔细斟酌每一处的细节,接下来让我们来感受排序算法的魅力吧!
交换排序
1.冒泡排序
思想:
两个相邻元素两两比较,依次向后,一趟确定一个元素位置。
说明:
冒泡排序有两层循环,第一层循坏是确定比较趟数,第二层循环确定元素位置,每确定一个元素的位置,检索数组长度减少一位。
示例:
这个数组其实第六趟已经有序了,但是程序还是会继续比较下去,因而可以设置一个状态值来判断数组是否已经有序,读者可以自行编写代码,这里不再展开。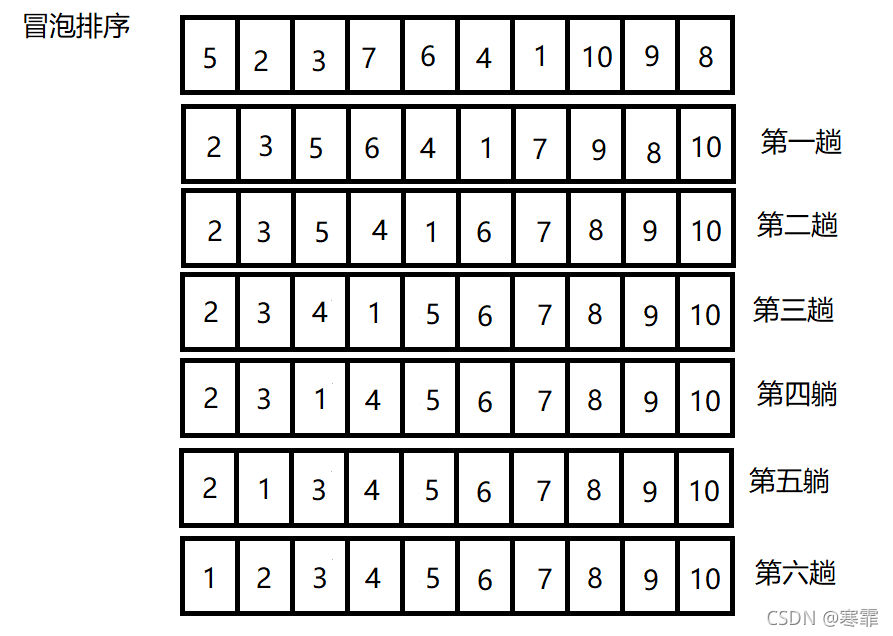
代码:
public void bubbleSort(int[] array){
for (int i = 0; i < array.length - 1; i++) {
for (int j = 0; j < array.length - 1 - i; j++) {
if(array[j] > array[j + 1]){
int temp = array[j];
array[j]= array[j + 1];
array[j + 1] = temp;
}
}
}
}
2.快速排序
思想:
以一个数为基准,把数组分为两段(比基准数小的为一段,比基准大的数为一段),此时基准数是有序的,再以这两段数组为新数组,递归下去,直到所有的基准数有序,也就是数组有序了。
说明:
快速排序对基准数的选择非常重要,如果每次基准数都能把数组对半分割,那么快速排序的时间复杂度为 O(N * log N) ,反过来,如果基准数每次都是在分割数组中最大的数,或者最小的数,那么数组分割效率非常低,此时的时间复杂度为 O( N ^ 2 ) 。
示例: 可以看到第三趟和第四躺一模一样,这是因为第三躺的基准数为数组中最小的数,因而排序时效率非常低,此时只能等待第二趟排序的右半排序来排序,由此可见基准数选取的重要性!这里强烈建议读者自己来走一遍代码,这样才能更加熟悉快速排序的排序时的代码流程。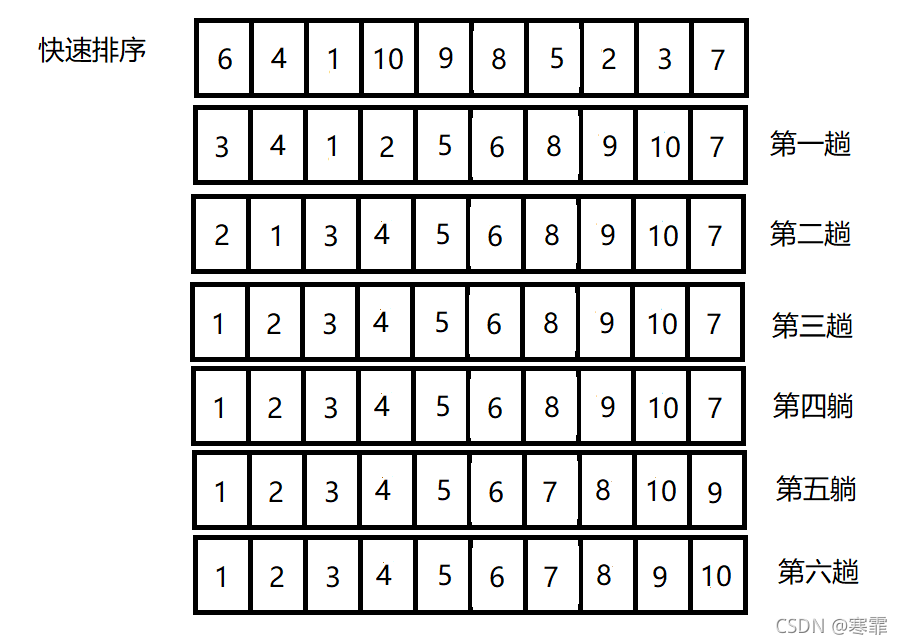
代码:
public int partition(int[] array, int low, int high) {
int pivot = array[low];
while (low < high) {
while (low < high && array[high] >= pivot) {
high--;
}
array[low] = array[high];
while (low < high && array[low] <= pivot) {
low++;
}
array[high] = array[low];
}
array[low] = pivot;
return low;
}
public void quick(int[] array, int start, int end) {
if (start >= end) {
return;
}
int pivot = partition(array, start, end);
quick(array, start, pivot - 1);
quick(array, pivot + 1, end);
}
public void quickSort(int[] array) {
quick(array, 0, array.length - 1);
}
插入排序
1.直接插入排序
思想:
每次保证数组检索到当前是有序的,直到检索完整个数组。
说明:
直接插入排序相对于其它的排序,变得智能了,而且就算当前的数组已经有序,它也能快速的跳出,因为它总能保证当前检索位置的前面所有元素全是有序的,因而它只要比较当前位置的前面一位就可以跳出本躺排序。
示例: 可以看到第六趟和第七躺一模一样,因为第六躺的时候第七个位置已经有序了,但这其实无关紧要,因为当前位置的前面所有元素一定是有序的,遇到这种情况也只是与前一个的元素比较一次罢了。
代码:
public void directInsertSort(int[] array){
for (int i = 1; i < array.length; i++) {
int j = i - 1;
int temp = array[i];
for (; j >= 0 && array[j] > temp; j--) {
array[j + 1] = array[j];
}
array[j + 1] = temp;
}
}
2.希尔排序
思想:
希尔排序是直接插入排序的优化版,与直接插入排序一样的思想一样,都是每次保证当前检索的数组有序。但是希尔排序是把数组分为多段,且每个数组的元素都是跳跃式的,这样的做法使得移动元素的速度大大提高。当当前的多段数组全部有序时,再次将数组分段,注意,每次分段数组的段数应该越来越少,最后一次是一段(全排序)。
说明:
希尔排序在排序大量的元素时,很有优势,移动元素速度很快,弥补了直接插入排序的不足,但是在排序少量的元素时,显得不尽人意。有时排序少量元素也很快(例如排为升序时,较小的元素基本在最后面,那么这些元素也能很快的排到前面去)。另外,关于 gap 的分段方式也直接影响希尔排序的效率(但是到目前为止,仍然没有一个很好的方式来规定 gap 的分段方式,这里以 gap = gap / 3 + 1 为例,但这仍然是一个不好的分段方式)。
示例: 注意,希尔排序分段数组时,在 gap位置从后向前取元素,而且有些元素很有可能多次被选取,这么做的目的就是让后面的数组中较小的元素能尽快排到前面去!可能说起来可能有点抽象,我很建议读者去跟着代码走一遍!这样才能体会到希尔排序的魅力!这里从过程来看,希尔排序确实有点难尽人意,但不要就此觉得希尔排序不堪一击,当排序的数据非常多时,希尔排序一定会让你惊掉下巴,因为它移动元素的速度实在太快了!
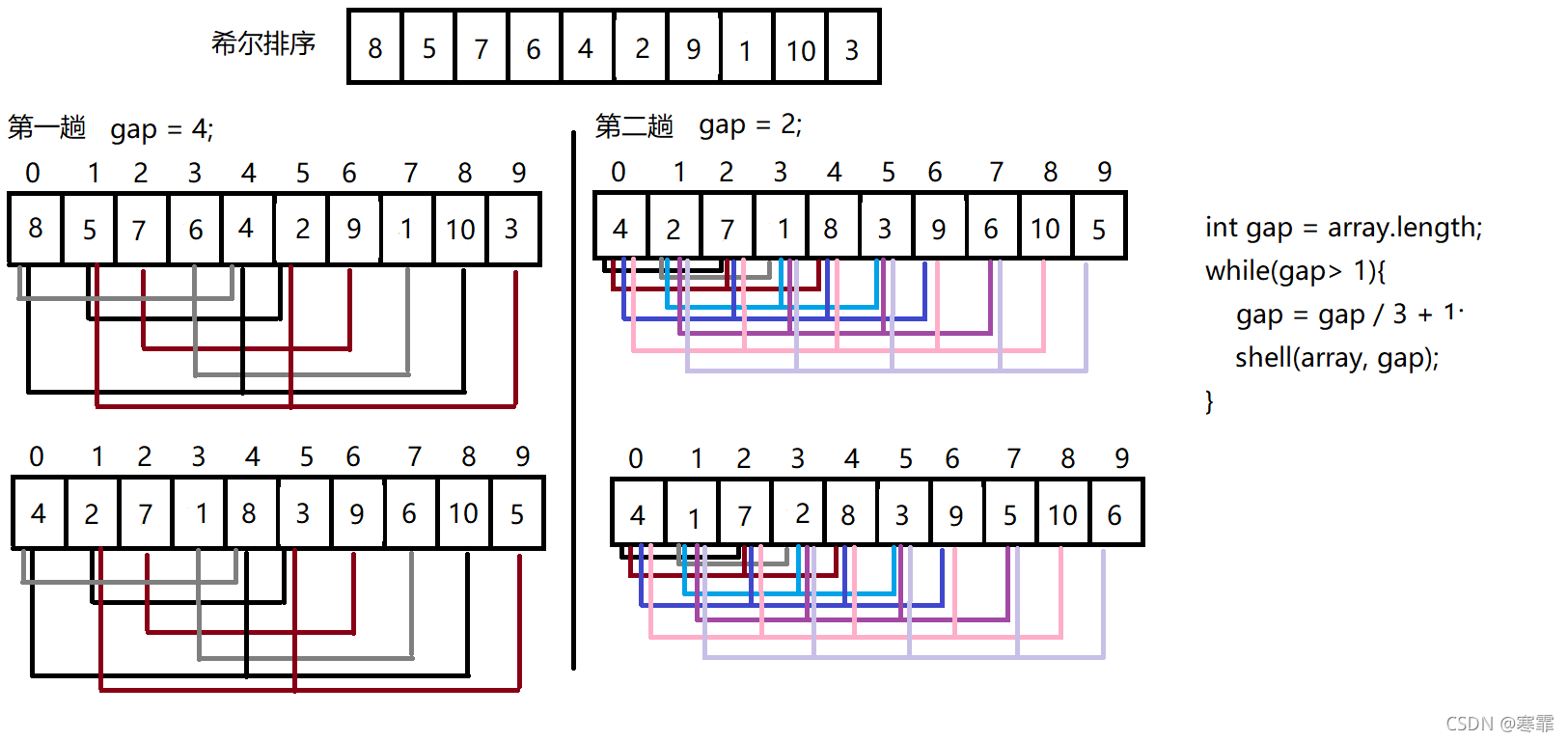

代码:
/**
* @param array 排序的数组
* @param gap 每段数组元素的间隔 也可以理解成组数
*/
public void shell(int[] array, int gap){
for (int i = gap; i < array.length; i++) {
int temp = array[i];
int j = i - gap;
for (; j >= 0 && array[j] > temp; j -= gap) {
array[j + gap] = array[j];
}
array[j + gap] = temp;
}
}
public void shellSort(int[] array){
int gap = array.length;
while(gap > 1){
gap = gap / 3 + 1;
shell(array,gap);
}
}
选择排序
1.简单选择排序:
思想:
第一个元素和第一个元素后面的所有的元素比较,确定第一个位置是有序的数,依次向后,直到每个位置都有序为止。
说明:
简单选择排序第一层循坏是确定比较趟数,第二层循坏是确定元素位置,每确定一个位置检索数组长度减一。
示例: 简单选择排序的比较趟数是确定的,可以看到第六躺和第七躺是一模一样的,因为第六躺时,正好第七个位置也有序了,但程序仍然会检索下去,此外第九躺和第十躺也是一样的(当然,这肯定可以优化,读者可自行展开)。
代码:
public void selectSort(int[] array){
for (int i = 0; i < array.length; i++) {
for (int j = i + 1; j < array.length; j++) {
if(array[i] > array[j]){
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
}
}
2.堆排序
思想:
堆排序利用了堆的自组织这个特点,让堆的堆顶元素与堆尾元素互换,然后堆尾元素有序,再让堆自组织长度减一,然后堆又自组织,再堆顶元素与堆尾元素互换,直到堆自组织长度为0,此时所有元素有序。
说明: 堆是一个极其精巧的数据结构,逻辑上是一个自组织的二叉树,底层物理上是一个优先级队列,二叉树父子节点之间总是存在 child = 2 * parent + 1; 或是 child = 2 * parent + 2; 这两种关系,利用这个来组织父子节点之间的数据,从而组织整个二叉树。
示例: 不要觉得堆排序繁琐,堆排序每次都是对半检索,检索的速度非常快,而且堆在逻辑上是一棵完全二叉树,不存在单分支树的情况,因而堆排序的效率是固定的,排序速度十分快!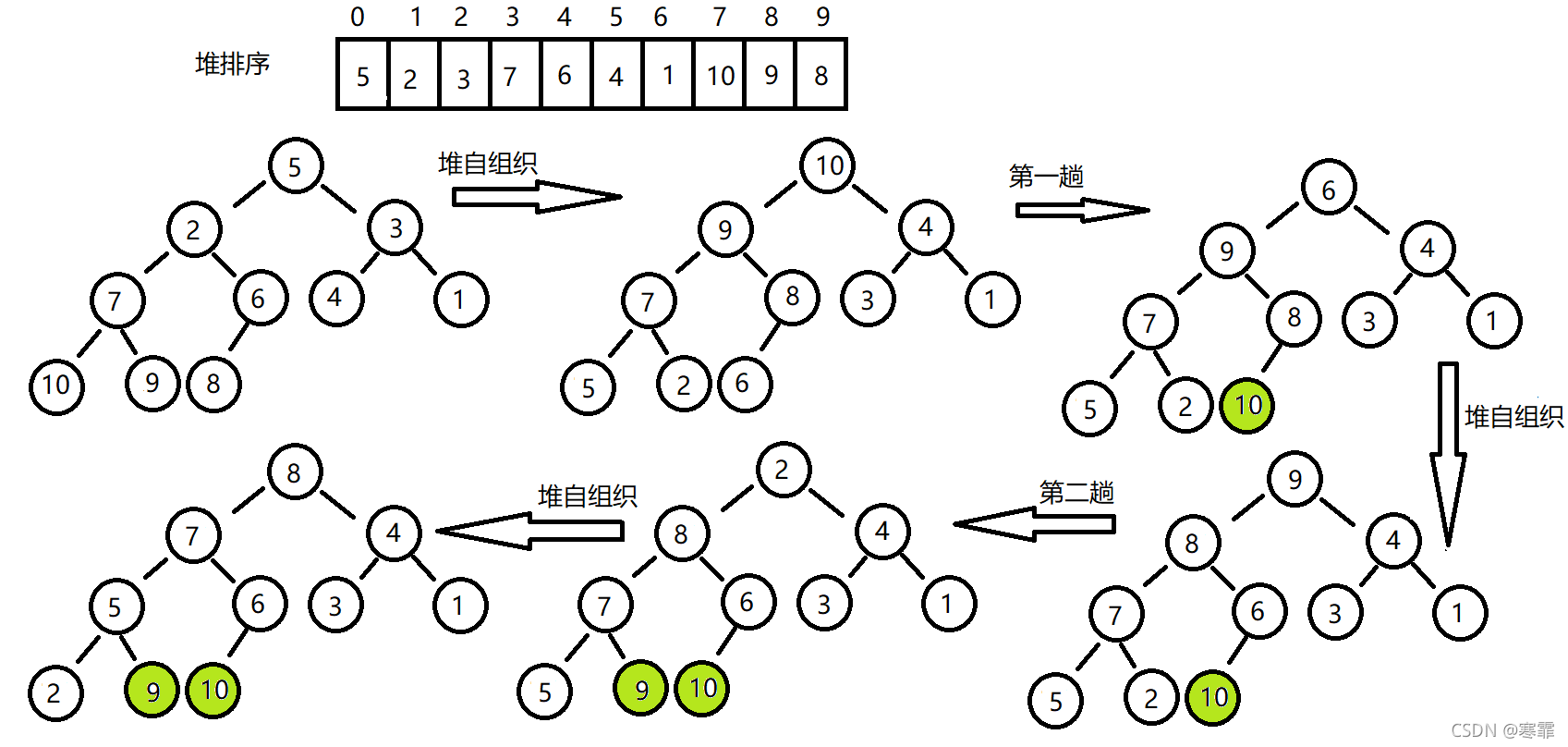


代码:
//建立大堆 从小到大排序
public void createHeap(int[] array) {
for (int i = (array.length - 1 - 1) / 2; i >= 0; i--) {
siftDown(array, i, array.length);
}
}
//堆的自组织
public void siftDown(int[] array, int root, int len) {
int parent = root;
int child = 2 * parent + 1;
while (child < len) {
if (child + 1 < len && array[child] < array[child + 1]) {
// 这里的child一定是兄弟节点中最大的元素。
child++;
}
if (array[child] > array[parent]) {
int temp = array[child];
array[child] = array[parent];
array[parent] = temp;
parent = child;
child = 2 * parent + 1;
} else {
break;
}
}
}
public void heapSort(int[] array) {
createHeap(array);
int end = array.length - 1;
while (end > 0) {
int temp = array[end];
array[end] = array[0];
array[0] = temp;
siftDown(array, 0, end);
end--;
}
}
归并排序
思想:
归并排序利用递归把数组分为长度为1和长度为2的片段,再回溯合并,使子片段依次有序,回溯大片段也有序.
说明:
归并排序让子数组全部有序,再对两个数组依次检索元素,合并成新数组,依次合并,直到所有数组全部合并完成。
示例: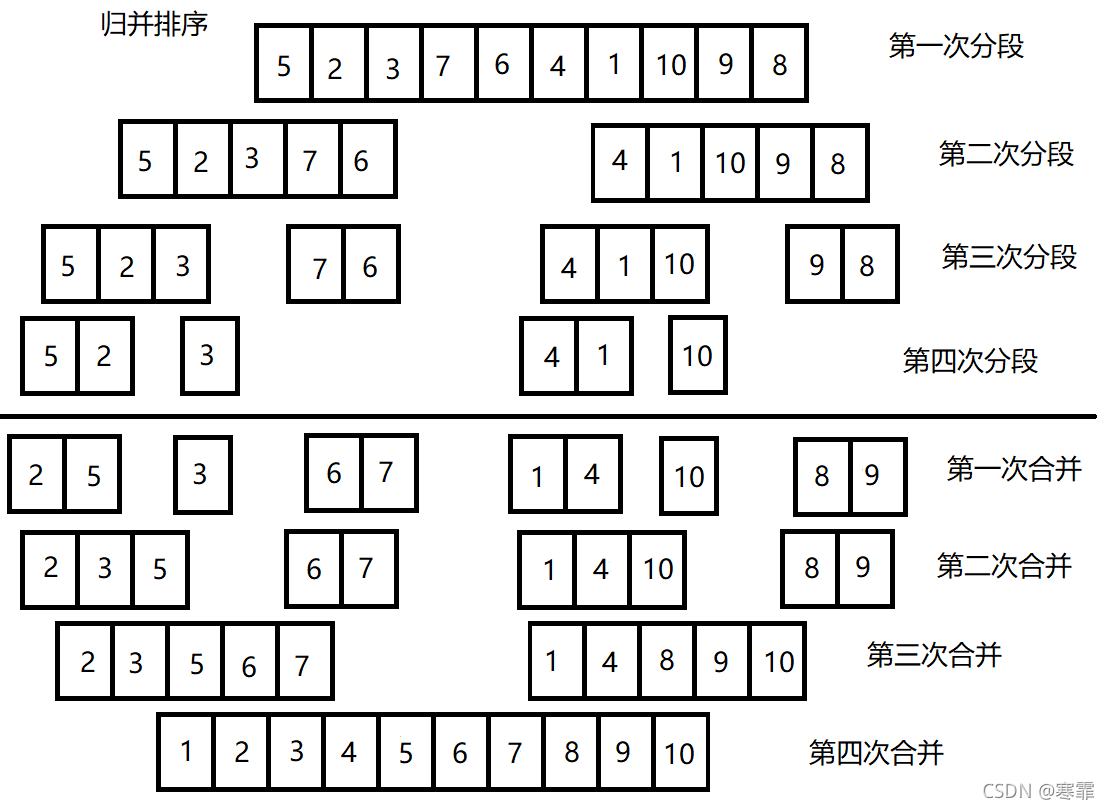
代码:
public void mergeSortInternal(int[] array, int low, int high){
if(low >= high){
return;
}
int mid = (low + high) / 2;
mergeSortInternal(array, low, mid);
mergeSortInternal(array, mid + 1, high);
//合并
merge(array, low, mid, high);
}
public void merge(int[] array, int low, int mid, int high){
int s1 = low;
int e1 = mid;
int s2 = mid + 1;
int e2 = high;
int[] temp = new int[high - low + 1];
int k = 0;
while(s1 <= e1 && s2 <= e2){
if(array[s1] <= array[s2]){
temp[k++] = array[s1++];
}else{
temp[k++] = array[s2++];
}
}
while(s1 <= e1){
temp[k++] = array[s1++];
}
while(s2 <= e2){
temp[k++] = array[s2++];
}
for (int i = 0; i < temp.length; i++) {
array[i + low] = temp[i];
}
}
public void mergeSort(int[] array){
mergeSortInternal(array, 0 ,array.length - 1);
}