一、定义
如果我们知道每幅影像的6个外方位元素,就能确定被摄物体与航摄影像的关系。因此,如何获取影像的外方位元素,一直是摄影测量工作者所探讨的问题。可采取的方法有:利用雷达、全球定位系统(GPS)、惯性导航系统(INS)以及星相摄影机来获取影像的外方位元素;也可利用影像覆盖范围内一定数量的控制点的空间坐标与影像坐标,根据共线方程反求该影像的外方位元素,这种方法称为单幅影像的空间后方交会。
二、基本流程
以单幅影像为基础,从该影像所覆盖地面范围内的若干控制点的已知地面坐标和相应点的像坐标量测值出发,根据共线条件方程,运用最小二乘间接平差,求解该影像在航空摄影时刻的外方位素
由于共线方程是非线性函数,为了运用最小二乘法,必须先将其线性化。
共线条件方程的线性化
某一点的共线方程为: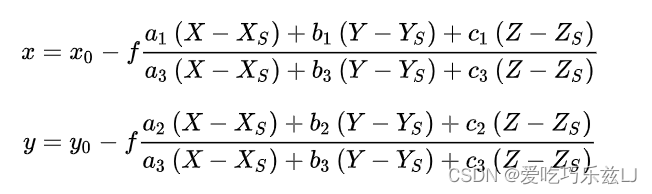
旋转矩阵R:

将共线方程在外方位元素近似值处一阶泰勒展开,得:
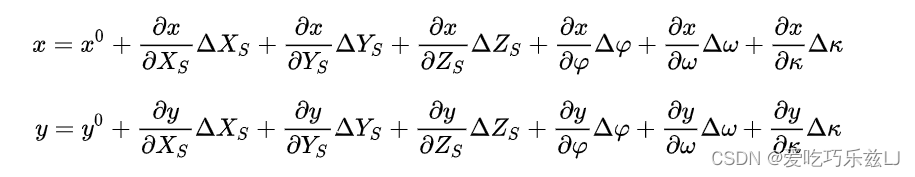
将控制点对应的像点的像平面坐标视为观测值,外方位元素视为参数,由共线方程的线性形式可列出误差方程:
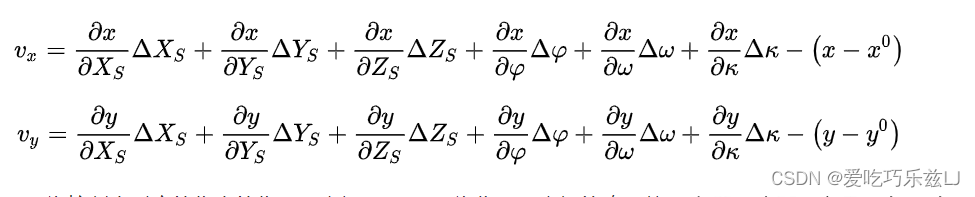
三、C#语言实现程序
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.IO;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;
namespace 空间后方交会1
{
public partial class Form1 : Form
{
string[][] zuobiao;
public double[,] zb1;//XYZ
double Xs0;
double Ys0;
double Zs0;
double[,] R;//旋转矩阵
double f0;
double[,] x0y0;//x0y0
double φ0 ;
double ω0 ;
double κ0 ;
public Form1()
{
InitializeComponent();
}
private void listView1_SelectedIndexChanged(object sender, EventArgs e)
{
}
private void button1_Click(object sender, EventArgs e)
{
string txt1 = "";
DialogResult de = openFileDialog1.ShowDialog();
//获取所打开文件的文件名
string filename = openFileDialog1.FileName;
if (de == System.Windows.Forms.DialogResult.OK && !string.IsNullOrEmpty(filename))
{
StreamReader sr = new StreamReader(filename);
txt1 = sr.ReadToEnd();
sr.Close();
}
string[] hang = txt1.Split(new string[] { "\r\n" }, StringSplitOptions.RemoveEmptyEntries);
string[][] hang1=new string[hang.Length][];
for (int i = 0; i < hang.Length; i++)
{
hang1[i] = hang[i].Split(',');
}
for (int i = 0; i < hang1.Length; i++)
{
ListViewItem item = new ListViewItem(hang1[i]);
listView1.Items.Add(item);
}
zuobiao = hang1;
double[,] zb2=new double[hang1.Length,3];
for (int i = 0; i < hang1.Length; i++)
{
for (int j = 0; j < 3; j++)
{
zb2[i, j] = Convert.ToDouble(hang1[i][j + 2]);
}
}
double[,] zb3=new double[hang1.Length,2];
for (int i = 0; i < hang.Length; i++)
{
for (int j = 0; j < 2; j++)
{
zb3[i, j] = Convert.ToDouble(hang1[i][j]);
}
}
zb1 = zb2;
x0y0= zb3;
}
private void listView1_MouseClick(object sender, MouseEventArgs e)
{
}
private void button2_Click(object sender, EventArgs e)
{
φ0 = 0;
ω0 = 0;
κ0 = 0;
Xs0 = zb(zuobiao, 2);
Ys0 = zb(zuobiao, 3);
double m0;
if (m.Text != "")
{
string[] mm = m.Text.Split('/');
m0 = Convert.ToDouble(mm[1]);
}
else
{
m0 = Math.Sqrt(Math.Pow(zb1[1, 0] - zb1[0, 0], 2) + Math.Pow(zb1[0, 1] - zb1[1, 1], 2)) / Math.Sqrt(Math.Pow(x0y0[1, 0] - x0y0[0, 0], 2) + Math.Pow(x0y0[1, 1] - x0y0[0, 1], 2))*1000;
m.Text = "1/"+m0.ToString();
}
f0=Convert.ToDouble(f.Text);
Zs0 = f0 * m0 / 1000;
Double[,] L;
double[,] B = new double[8, 6];
double[,] X;
int I = 0;
while (true)
{
//迭代
R = RR(φ0, ω0, κ0);
L = lxly(x0y0);
//double φ0;
//double ω0;
//double κ0;
for (int i = 0; i < 4; i++)
{
B[2 * i, 0] = (R[0, 0] * f0 + R[2, 0] * x0y0[i, 0]) / (R[2, 0] * (zb1[i, 0] - Xs0) + R[2, 1] * (zb1[i, 1] - Ys0) + R[2, 2] * (zb1[i, 2] - Zs0));
B[2 * i, 1] = (R[0, 1] * f0 + R[2, 1] * x0y0[i, 0]) / (R[2, 0] * (zb1[i, 0] - Xs0) + R[2, 1] * (zb1[i, 1] - Ys0) + R[2, 2] * (zb1[i, 2] - Zs0));
B[2 * i, 2] = (R[0, 2] * f0 + R[2, 2] * x0y0[i, 0]) / (R[2, 0] * (zb1[i, 0] - Xs0) + R[2, 1] * (zb1[i, 1] - Ys0) + R[2, 2] * (zb1[i, 2] - Zs0));
B[2 * i + 1, 0] = (R[1, 0] * f0 + R[2, 0] * x0y0[i, 1]) / (R[2, 0] * (zb1[i, 0] - Xs0) + R[2, 1] * (zb1[i, 1] - Ys0) + R[2, 2] * (zb1[i, 2] - Zs0));
B[2 * i + 1, 1] = (R[1, 1] * f0 + R[2, 1] * x0y0[i, 1]) / (R[2, 0] * (zb1[i, 0] - Xs0) + R[2, 1] * (zb1[i, 1] - Ys0) + R[2, 2] * (zb1[i, 2] - Zs0));
B[2 * i + 1, 2] = (R[1, 2] * f0 + R[2, 2] * x0y0[i, 1]) / (R[2, 0] * (zb1[i, 0] - Xs0) + R[2, 1] * (zb1[i, 1] - Ys0) + R[2, 2] * (zb1[i, 2] - Zs0));
B[2 * i, 3] = x0y0[i, 1] * Math.Sin(ω0) - (x0y0[i, 0] * (x0y0[i, 0] * Math.Cos(κ0) - x0y0[i, 1] * Math.Sin(κ0)) / f0 + f0 * Math.Cos(κ0)) * Math.Cos(ω0);
B[2 * i, 4] = -f0 * Math.Sin(κ0) - x0y0[i, 0] * (x0y0[i, 0] * Math.Sin(κ0) + x0y0[i, 1] * Math.Cos(κ0)) / f0;
B[2 * i, 5] = x0y0[i, 1];
B[2 * i + 1, 3] = -x0y0[i, 0] * Math.Sin(ω0) - (x0y0[i, 1] * (x0y0[i, 0] * Math.Cos(κ0) - x0y0[i, 1] * Math.Sin(κ0)) / f0 - f0 * Math.Sin(κ0)) * Math.Cos(ω0);
B[2 * i + 1, 4] = -f0 * Math.Cos(κ0) - x0y0[i, 1] * (x0y0[i, 0] * Math.Sin(κ0) + x0y0[i, 1] * Math.Cos(κ0)) / f0;
B[2 * i + 1, 5] = -x0y0[i, 0];
}
X = Matrix.matrix.Transpose(B);
X = Matrix.matrix.Athwart(Matrix.matrix.MultiplyMatrix(X, B));
X = Matrix.matrix.MultiplyMatrix(X, Matrix.matrix.Transpose(B));
X = Matrix.matrix.MultiplyMatrix(X, L);
Xs0 += X[0, 0];
Ys0 += X[1, 0];
Zs0 += X[2, 0];
φ0 += X[3, 0];
ω0 += X[4, 0];
κ0 += X[5, 0];
I++;
if (Math.Abs(X[0,0])<Convert.ToDouble(xian.Text)&& Math.Abs(X[1, 0]) < Convert.ToDouble(xian.Text)&& Math.Abs(X[2, 0]) < Convert.ToDouble(xian.Text)&& Math.Abs(X[3, 0]) < Convert.ToDouble(jiao.Text) && Math.Abs(X[4, 0]) < Convert.ToDouble(jiao.Text) && Math.Abs(X[5, 0]) < Convert.ToDouble(jiao.Text))
{
break;
}
}
textBox1.Text = "Xs=" + Xs0.ToString() + "\r\n" + "Ys=" + Ys0.ToString() + "\r\n" + "Zs=" + Zs0.ToString() + "\r\n" +
"φ=" + DMS(φ0).ToString() + "\r\n" + "ω=" + DMS(ω0).ToString() + "\r\n" + "κ=" + DMS(κ0).ToString();
label7.Text = "迭代次数:"+I.ToString();
}
static public double DMS(double ang)
{
int fuhao = 1;
if (ang < 0)
{
fuhao = -1;
ang = -ang;
}
ang = ang * 180.0 / Math.PI + 2.78E-10;//加 1.0E-6 秒
int d = (int)ang;
ang = (ang - d) * 60.0;
int m = (int)ang;
double s = (ang - m) * 60.0 - 1.0E-6;//减 1.0E-6 秒
if (s < 0) s = 0;
return (d + m / 100.0 + s / 10000.0) * fuhao;
}
public double zb(string[][] s,int i)
{
double sum = 0;
for (int k = 0; k <s.Length ; k++)
{
sum+=Convert.ToDouble(s[k][i]);
}
return sum/s.Length;
}
public double[,]RR(double a,double b,double c)//旋转R
{
double[,] R1=new double[3,3];
R1[0,0] = Math.Cos(a)*Math.Cos(c)-Math.Sin(a)*Math.Sin(b)*Math.Sin(c);
R1[1, 0] = -Math.Cos(a) * Math.Sin(c) - Math.Sin(a) * Math.Sin(b) * Math.Cos(c);
R1[2, 0] = -Math.Sin(a) * Math.Cos(b);
R1[0, 1] = Math.Cos(b) * Math.Sin(c);
R1[1,1]= Math.Cos(b) * Math.Cos(c);
R1[2, 1] = -Math.Sin(b);
R1[0, 2] = Math.Sin(a) * Math.Cos(c) + Math.Cos(a) * Math.Sin(b) * Math.Sin(c);
R1[1, 2] = -Math.Sin(a) * Math.Sin(c) + Math.Cos(a) * Math.Sin(b) * Math.Cos(c);
R1[2, 2] = Math.Cos(a) * Math.Cos(b);
return R1;
}
public double[,]lxly(double[,] a)//lxly
{
double[,] L = new double[zuobiao.Length * 2, 1];
double[,] LL = LL0(R, zb1, f0);
int j = 0;
for (int i = 0; i < zuobiao.Length; i++)
{
L[j, 0] = a[i,0]-LL[j,0];
j++;
L[j, 0] = a[i, 1] - LL[j, 0];
j++;
}
return L;
}
public double[,] LL0(double [,] a,double[,] b,double f)
{
double[,] L = new double[zuobiao.Length * 2, 1];
L[0,0]= -f * (a[0, 0] * (b[0, 0] - Xs0) + a[0, 1] * (b[0, 1] - Ys0) + a[0, 2] * (b[0, 2] - Zs0)) / (a[2, 0] * (b[0, 0] - Xs0) + a[2, 1] * (b[0, 1] - Ys0) + a[2, 2] * (b[0, 2] - Zs0));
L[1, 0] = -f * (a[1, 0] * (b[0, 0] - Xs0) + a[1, 1] * (b[0, 1] - Ys0) + a[1, 2] * (b[0, 2] - Zs0)) / (a[2, 0] * (b[0, 0] - Xs0) + a[2, 1] * (b[0, 1] - Ys0) + a[2, 2] * (b[0, 2] - Zs0));
L[2, 0] = -f * (a[0, 0] * (b[1, 0] - Xs0) + a[0, 1] * (b[1, 1] - Ys0) + a[0, 2] * (b[1, 2] - Zs0)) / (a[2, 0] * (b[1, 0] - Xs0) + a[2, 1] * (b[1, 1] - Ys0) + a[2, 2] * (b[1, 2] - Zs0));
L[3, 0] = -f * (a[1, 0] * (b[1, 0] - Xs0) + a[1, 1] * (b[1, 1] - Ys0) + a[1, 2] * (b[1, 2] - Zs0)) / (a[2, 0] * (b[1, 0] - Xs0) + a[2, 1] * (b[1, 1] - Ys0) + a[2, 2] * (b[1, 2] - Zs0));
L[4, 0] = -f * (a[0, 0] * (b[2, 0] - Xs0) + a[0, 1] * (b[2, 1] - Ys0) + a[0, 2] * (b[2, 2] - Zs0)) / (a[2, 0] * (b[2, 0] - Xs0) + a[2, 1] * (b[2, 1] - Ys0) + a[2, 2] * (b[2, 2] - Zs0));
L[5, 0] = -f * (a[1, 0] * (b[2, 0] - Xs0) + a[1, 1] * (b[2, 1] - Ys0) + a[1, 2] * (b[2, 2] - Zs0)) / (a[2, 0] * (b[2, 0] - Xs0) + a[2, 1] * (b[2, 1] - Ys0) + a[2, 2] * (b[2, 2] - Zs0));
L[6, 0] = -f * (a[0, 0] * (b[3, 0] - Xs0) + a[0, 1] * (b[3, 1] - Ys0) + a[0, 2] * (b[3, 2] - Zs0)) / (a[2, 0] * (b[3, 0] - Xs0) + a[2, 1] * (b[3, 1] - Ys0) + a[2, 2] * (b[3, 2] - Zs0));
L[7, 0] = -f * (a[1, 0] * (b[3, 0] - Xs0) + a[1, 1] * (b[3, 1] - Ys0) + a[1, 2] * (b[3, 2] - Zs0)) / (a[2, 0] * (b[3, 0] - Xs0) + a[2, 1] * (b[3, 1] - Ys0) + a[2, 2] * (b[3, 2] - Zs0));
return L;
}
private void f_TextChanged(object sender, EventArgs e)
{
}
private void button3_Click(object sender, EventArgs e)
{
double[,] xy = LL0(R, zb1, f0);
string sum = "";
for (int i = 0; i < 8; i++)
{
sum += xy[i, 0] + "\r\n";
}
textBox1.Text = sum;
}
}
}使用到的矩阵计算的类
using System;
namespace Matrix
{
class matrix
{
/// <summary>
/// 求矩阵的秩,改变了原矩阵
/// </summary>
/// <param name= "iMatrix "> </param>
/// <returns> </returns>
public static int OrderCount(double[,] iMatrix)
{
int i = 0;
for (i = 0; i < 3; i++)
{
if (iMatrix[i, i] != 0)
{
double intTemp = iMatrix[i, i];
for (int j = 0; j < 3; j++)
{
iMatrix[i, j] = iMatrix[i, j] / intTemp;
}
}
for (int j = 0; j < 3; j++)
{
if (j == i)
continue;
double intTemp = iMatrix[j, i];
for (int k = 0; k < 3; k++)
{
iMatrix[j, k] = iMatrix[j, k] - iMatrix[i, k] * intTemp;
}
}
}
for (i = 0; i < 3; i++)
if (iMatrix[i, i] == 0)
break;
return i;
}
/// <summary>
/// 求矩阵的秩,不改变原矩阵
/// </summary>
/// <param name= "iMatrix "> </param>
/// <returns> </returns>
public static int OrderCountNotChange(double[,] iMatrix)
{
double[,] TempMatrix = new double[3, 3];
int i = 0;
for (i = 0; i < 3; i++)
for (int j = 0; j < 3; j++)
TempMatrix[i, j] = iMatrix[i, j];
for (i = 0; i < 3; i++)
{
if (TempMatrix[i, i] != 0)
{
double intTemp = TempMatrix[i, i];
for (int j = 0; j < 3; j++)
{
TempMatrix[i, j] = TempMatrix[i, j] / intTemp;
}
}
for (int j = 0; j < 3; j++)
{
if (j == i)
continue;
double intTemp = TempMatrix[j, i];
for (int k = 0; k < 3; k++)
{
TempMatrix[j, k] = TempMatrix[j, k] - TempMatrix[i, k] * intTemp;
}
}
}
for (i = 0; i < 3; i++)
if (TempMatrix[i, i] == 0)
break;
return i;
}
/// <summary>
/// 矩阵的转置
/// </summary>
/// <param name= "iMatrix "> </param>
public static double[,] Transpose(double[,] iMatrix)
{
int row = iMatrix.GetLength(0);
int column = iMatrix.GetLength(1);
//double[,] iMatrix = new double[column, row];
double[,] TempMatrix = new double[row, column];
double[,] iMatrixT = new double[column, row];
for (int i = 0; i < row; i++)
{
for (int j = 0; j < column; j++)
{
TempMatrix[i, j] = iMatrix[i, j];
}
}
for (int i = 0; i < column; i++)
{
for (int j = 0; j < row; j++)
{
iMatrixT[i, j] = TempMatrix[j, i];
}
}
return iMatrixT;
}
/// <summary>
/// 矩阵的逆矩阵
/// </summary>
/// <param name= "iMatrix "> </param>
public static double[,] Athwart(double[,] iMatrix)
{
int i = 0;
int row = iMatrix.GetLength(0);
double[,] MatrixZwei = new double[row, row * 2];
double[,] iMatrixInv = new double[row, row];
for (i = 0; i < row; i++)
{
for (int j = 0; j < row; j++)
{
MatrixZwei[i, j] = iMatrix[i, j];
}
}
for (i = 0; i < row; i++)
{
for (int j = row; j < row * 2; j++)
{
MatrixZwei[i, j] = 0;
if (i + row == j)
MatrixZwei[i, j] = 1;
}
}
for (i = 0; i < row; i++)
{
if (MatrixZwei[i, i] != 0)
{
double intTemp = MatrixZwei[i, i];
for (int j = 0; j < row * 2; j++)
{
MatrixZwei[i, j] = MatrixZwei[i, j] / intTemp;
}
}
for (int j = 0; j < row; j++)
{
if (j == i)
continue;
double intTemp = MatrixZwei[j, i];
for (int k = 0; k < row * 2; k++)
{
MatrixZwei[j, k] = MatrixZwei[j, k] - MatrixZwei[i, k] * intTemp;
}
}
}
for (i = 0; i < row; i++)
{
for (int j = 0; j < row; j++)
{
iMatrixInv[i, j] = MatrixZwei[i, j + row];
}
}
return iMatrixInv;
}
/// <summary>
/// 矩阵加法
/// </summary>
/// <param name= "MatrixEin "> </param>
/// <param name= "MatrixZwei "> </param>
public static double[,] AddMatrix(double[,] MatrixEin, double[,] MatrixZwei)
{
double[,] MatrixResult = new double[MatrixEin.GetLength(0), MatrixZwei.GetLength(1)];
for (int i = 0; i < MatrixEin.GetLength(0); i++)
for (int j = 0; j < MatrixZwei.GetLength(1); j++)
MatrixResult[i, j] = MatrixEin[i, j] + MatrixZwei[i, j];
return MatrixResult;
}
/// <summary>
/// 矩阵减法
/// </summary>
/// <param name= "MatrixEin "> </param>
/// <param name= "MatrixZwei "> </param>
public static double[,] SubMatrix(double[,] MatrixEin, double[,] MatrixZwei)
{
double[,] MatrixResult = new double[MatrixEin.GetLength(0), MatrixZwei.GetLength(1)];
for (int i = 0; i < MatrixEin.GetLength(0); i++)
for (int j = 0; j < MatrixZwei.GetLength(1); j++)
MatrixResult[i, j] = MatrixEin[i, j] - MatrixZwei[i, j];
return MatrixResult;
}
/// <summary>
/// 矩阵乘法
/// </summary>
/// <param name= "MatrixEin "> </param>
/// <param name= "MatrixZwei "> </param>
public static double[,] MultiplyMatrix(double[,] MatrixEin, double[,] MatrixZwei)
{
double[,] MatrixResult = new double[MatrixEin.GetLength(0), MatrixZwei.GetLength(1)];
for (int i = 0; i < MatrixEin.GetLength(0); i++)
{
for (int j = 0; j < MatrixZwei.GetLength(1); j++)
{
for (int k = 0; k < MatrixEin.GetLength(1); k++)
{
MatrixResult[i, j] += MatrixEin[i, k] * MatrixZwei[k, j];
}
}
}
return MatrixResult;
}
/// <summary>
/// 矩阵对应行列式的值
/// </summary>
/// <param name= "MatrixEin "> </param>
/// <returns> </returns>
public static double ResultDeterminant(double[,] MatrixEin)
{
return MatrixEin[0, 0] * MatrixEin[1, 1] * MatrixEin[2, 2] + MatrixEin[0, 1] * MatrixEin[1, 2] * MatrixEin[2, 0] + MatrixEin[0, 2] * MatrixEin[1, 0] * MatrixEin[2, 1]
- MatrixEin[0, 2] * MatrixEin[1, 1] * MatrixEin[2, 0] - MatrixEin[0, 1] * MatrixEin[1, 0] * MatrixEin[2, 2] - MatrixEin[0, 0] * MatrixEin[1, 2] * MatrixEin[2, 1];
}
}
public class myMatrix
{
/// <summary>
/// 矩阵的行数
/// </summary>
public int row
{
get
{
return MatrixEin.GetLength(0);
}
}
/// <summary>
/// 矩阵的列数
/// </summary>
public int column
{
get
{
return MatrixEin.GetLength(1);
}
}
/// <summary>
/// 用二维数组储存的矩阵
/// </summary>
public double[,] MatrixEin;
public myMatrix(int r, int c)
{
MatrixEin = new double[r, c];
}
/// <summary>
/// 用二维数组初始化行列式
/// </summary>
public myMatrix(double[,] m)
{
MatrixEin = new double[m.GetLength(0), m.GetLength(1)];
for (int i = 0; i < row; i++)
{
for (int j = 0; j < column; j++)
{
MatrixEin[i, j] = m[i, j];
}
}
}
/// <summary>
/// 用一维数组初始化为行向量
/// </summary>
public myMatrix(double[] m1)
{
MatrixEin = new double[1, m1.Length];
for (int i = 0; i < m1.Length; i++)
{
MatrixEin[0, i] = m1[i];
}
}
/// <summary>
/// 转置
/// </summary>
public myMatrix T
{
get
{
return new myMatrix(matrix.Transpose(MatrixEin));
}
}
/// <summary>
/// 行列式值
/// </summary>
public double R
{
get
{
return matrix.ResultDeterminant(MatrixEin);
}
}
/// <summary>
/// 返回这个矩阵的逆矩
/// </summary>
public myMatrix A
{
get
{
return new myMatrix(matrix.Athwart(MatrixEin));
}
}
/// <summary>
/// 矩阵加法
/// </summary>
static public myMatrix operator +(myMatrix m1, myMatrix m2)
{
if (m1.row != m2.row || m1.column != m2.column)
{
throw new Exception("无法运算");
}
var d = matrix.AddMatrix(m1.MatrixEin, m2.MatrixEin);
return new myMatrix(d);
}
/// <summary>
/// 矩阵减法
/// </summary>
static public myMatrix operator -(myMatrix m1, myMatrix m2)
{
if (m1.row != m2.row || m1.column != m2.column)
{
throw new Exception("无法运算");
}
var d = matrix.SubMatrix(m1.MatrixEin, m2.MatrixEin);
return new myMatrix(d);
}
/// <summary>
/// 矩阵乘法
/// </summary>
static public myMatrix operator *(myMatrix m1, myMatrix m2)
{
if (m1.column != m2.row)
{
throw new Exception("无法运算");
}
var d = matrix.MultiplyMatrix(m1.MatrixEin, m2.MatrixEin);
return new myMatrix(d);
}
/// <summary>
/// 矩阵数乘
/// </summary>
static public myMatrix operator *(double d, myMatrix m2)
{
myMatrix m = new myMatrix(m2.MatrixEin);
for (int i = 0; i < m.row; i++)
{
for (int j = 0; j < m.column; j++)
{
m.MatrixEin[i, j] *= d;
}
}
return m;
}
public override string ToString()
{
string s = "";
for (int i = 0; i < row; i++)
{
for (int j = 0; j < column; j++)
{
s += MatrixEin[i, j] + " ";
}
s += "\n";
}
return s;
}
}
}四、具体实例
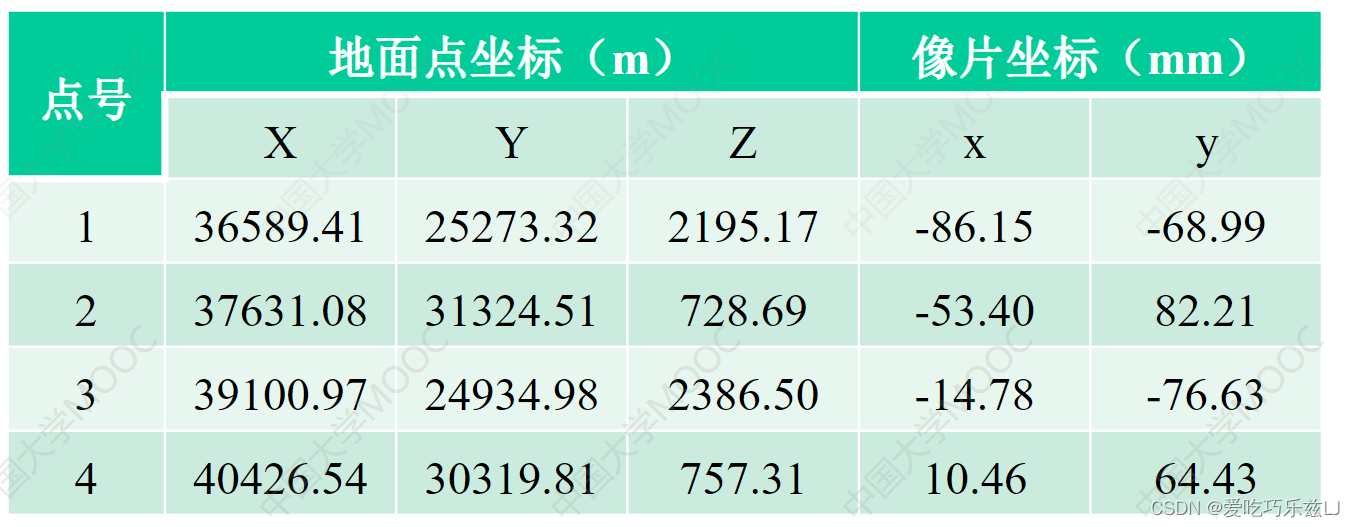
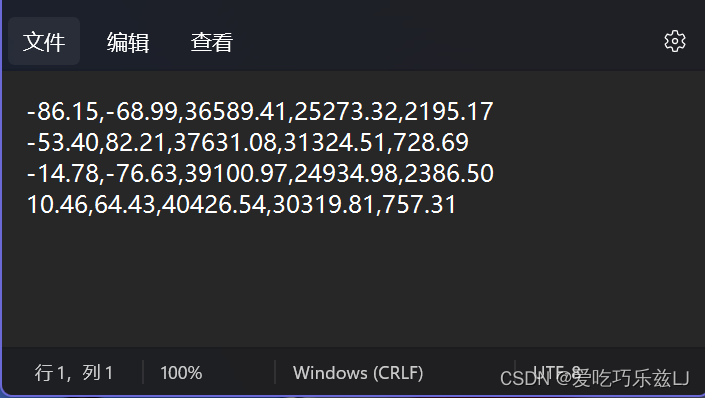
已知摄影机主距 f=153.24mm,四对点的像点坐标与相应的地面点坐标如下表:
计算近似垂直摄影情况下的后方交会解。
五、程序实现结果
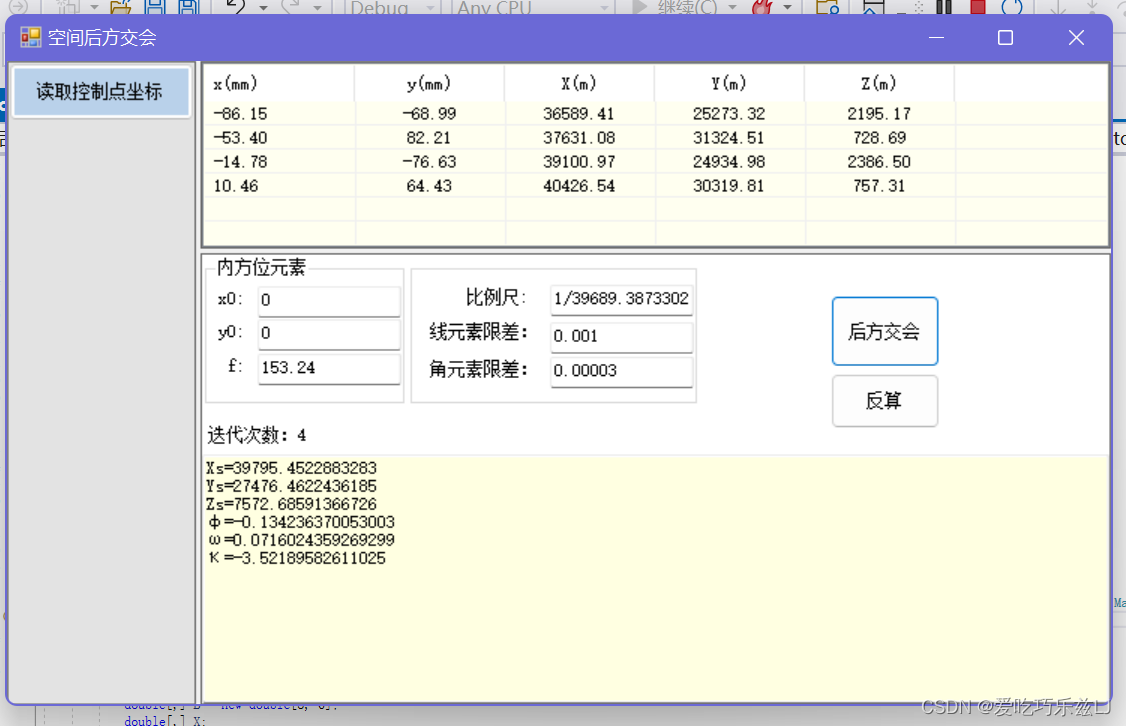
版权声明:本文为m0_71164917原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。