本文旨在记录算法笔记学习过程中的收获和一些知识点，部分易错知识点只针对个人而言，CCF-CSP考试冲鸭！！！

Chapter 2 C/C++快速入门（易错知识点）

2.1 基本数据类型

变量定义注意区分大小写。

一、整型

整型int，32bit（4Byte），取值范围是 $-2^{31}\sim (2^{31}-1)$ ，绝对值在 $10^{9}$ 范围内的整数都可以定义成int。

长整型long long，64bit（8Byte），取值范围是 $-2^{63}\sim(2^{63}-1)$ ，绝对值超过 $2.1\times 10^{9}$ 的整数就需要用long long存储。

如果long long型赋大于 $2^{31}-1$ 的初值，则需要在初值后加上LL，否则编译错误。

二、浮点型

单精度浮点float，取值范围 $-2^{128} \sim 2^{128}$ ，有效精度只有6~7位。

双精度浮点double，取值范围 $-2^{1024}\sim2^{1024}$ ,有效精度有15~16位。

尽量不要使用float，浮点型数据使用double存储。

2.2 顺序结构

一、使用scanf和printf输入/输出

scanf的%c是可以读入空格和换行的，因此在scanf的格式符选择上一定要注意是否能够正确读入需要输入的数据。

scanf对除%c以外，其他格式符的输入以空白符（空格、Tab）为结束判断标志；字符数组使用%s读入时以空格跟换行为读入结束标志。例如：

char str[10];
scanf("%s",str);
printd("%s",str);

上述代码段运行时，输入/输出结果如下：

//输入数据：
abcd efg
//输出数据：
abcd

即，abcd和efg之间的空格作为了scanf()读入字符数组结束的标志。

常用的输出格式：

（1）%md：使不足m位的int型变量以m位右对齐输出，高位以空格补齐；多于m位的变量原样输出。

（2）%0md：使不足m位的int型变量以m位右对齐输出，高位以0补齐；多于m位的变量原样输出。

（3）%.mf：让浮点数保留m位小数输出，舍入规则：“四舍六入五成双”。

2.5 数组

2.5.4 memset——对数组的每个元素赋相同的值

使用memset( )必须在程序开头添加string.h头文件。使用格式：

memset(数组名，值，sizeof(数组名))

注意：memset( )是按字节赋值！

2.7 指针

2.7.5 引用（c++）

引用（&）不产生副本，只是给原变量取了别名。

对引用变量的操作就是对原变量的操作。

使用引用变量简化了指针的使用。

2.8 结构体

2.8.3 结构体的初始化

*引入c++的构造函数进行初始化，可以简化结构体的初始化操作。

一、构造函数

在结构体中定义的，用于初始化结构体的一种函数。

特点：不需要写返回类型，函数名与结构体名相同。

一个结构体可以有多个构造函数，可以对部分结构体内变量进行初始化。

struct studentInfo{
    int id;
    char gender;
    //默认生成的构造函数
    studentInfo(){}
    //只初始化gender
    studentInfo(char _gender){
        gender = _gender;    
    }
    //初始化id和gender
    studentInfo(int _id,char _gender){
        id = _id;
        gender = _gender;
    }
};

注意：1.如果自定义了构造函数，不能不经初始化就定义结构体变量。（此时默认的构造函数已经不存在）

2. 只要参数个数不同，可以定义多个构造函数。

Chapter 3 入门模拟

3.1 简单模拟

PAT B1032 挖掘机技术哪家强

//题目请查看PAT官网https://pintia.cn/problem-sets/994805260223102976/problems/994805289432236032
//利用数组即可实现相应功能

int scores[MAXN] = {0};
int main() {
	int i = 0, N = 0;
	int school = 0, score = 0;
	scanf("%d", &N);
	for (i = 0; i < N; i++) {
		scanf("%d%d", &school, &score);
		scores[school] += score;
	}
	int flag = 0, max = 0;
	for (i = 1; i <= N; i++) {
        //这里循环条件必须是1~N，否则测试点2，不能通过测试
		if (scores[i] > max) {
			flag = i;
			max = scores[i];
		}
	}
	printf("%d %d", flag, max);
	return 0;
}

3.4 日期处理

codeup 1928 日期差值

解决日期差值问题，只需要通过增加小日期，通过比较day和当月日期，month和12的大小关系，实现月、年的增加即可，注意控制条件。

int isleapyear(int year);

int month[13][2] = {
	{0,0},{31,31},{28,29},{31,31},{30,30},{31,31},{30,30},
	{31,31},{31,31},{30,30},{31,31},{30,30},{31,31}
};
//用于存储平年（第0维）和闰年（第1维）各月的天数

int main() {
	int date1 = 0, date2 = 0;
	int year = 0, mon = 0;
	int day = 0, leap = 0;
	while (scanf("%d%d",&date1,&date2) != EOF) {
		if (date1 > date2) {
			int temp = date1;
			date1 = date2;
			date2 = temp;
		}
		int count = 1;
		while (date1 != date2) {
			count++;
			date1++;
			year = date1 / 10000;
			mon = (date1 % 10000) / 100;
			day = date1 % 100;
			leap = isleapyear(year);
			if (day > month[mon][leap]) {
				date1 = year * 10000 + (mon + 1) * 100 + 1;
			}//如果day的值超过了本月最大天数，月数增加
			year = date1 / 10000;
			mon = (date1 % 10000) / 100;
			if (mon > 12) {
				date1 = (year + 1) * 10000 + 101;
			}//如果mon的值大于12，年份增加
		}
		printf("%d\n", count);
	}
}

int isleapyear(int year) {
	if ((year % 100 != 0&& year % 4 == 0) || year % 400 == 0) {
		return 1;
	}
	return 0;
}

2021.08.12

Chapter 4 算法初步

4.1 排序

4.1.1 选择排序

简单选择排序：进行n趟操作，每趟从待排序的部分[i,n]选择最小的（或最大，由升序或者降序决定）元素，令其与A[i]交换，则[0,i]就变得有序了。

总的时间复杂度为O(n^2)。

4.1.2 插入排序

直接插入排序：对A[1~n]，令i=2开始枚举，进行n-1趟操作，每次将第i位插入到有序部分A[1~i-1]。

4.1.3 sort函数应用

参见第6.9.6节。

4.2 散列

4.2.1 散列（hash）定义与整数散列

将元素（key）通过一个函数（H）转换为整数，使得该整数可以尽量唯一地代表这个元素。

除留余数法：

H(key)=key%mod（mod一般直接取表长Tsize）

因为对于不同key的hash值可能相同，所以需要解决冲突：

1. 线性探查法：

依次探查H(key)+i（i=1,2,...）是否被占用。超过表长则回到0开始探查。

2. 平方探查法：

依次探查H(key)+i^2是否被占用，注意不能是负数，对于负数对表长求模。

3. 链地址法：

将H(key)相同的key连接成一个单链表。

4.2.2 字符串hash初步

将字母A~Z，a~z表示为进制数，如字符串中只含有A~Z，则转换为26进制数，再将其用于hash计算。

4.3 递归

4.3.1 分治

分解-解决-合并。

4.3.2 递归

递归边界、递归式

n皇后问题。

4.4 贪心

4.4.1 简单贪心

贪心法：考虑在当前状态下局部最优（或较优）的策略。来使全局的结果达到最优（或较优）

4.5 二分

4.5.3 快速幂

例如求 $a^{b}%m$ ,利用常规循环求解的时间复杂度是O(b)。

快速幂解法：基于二分思想

1. 如果b是奇数，有 $a^{b}=a*a^{b-1}$

2. 如果b是偶数，有 $a=a^{b/2}*a^{b/2}$

在经过log(b)级别次数转换后，可以把b变成0；任何正整数的0次方是1。

快速幂的递归写法：

typedef long long LL;
//求a^b%m递归写法
LL binaryPow(LL a, LL b, LL m) {
	if (b == 0) return 1;
	if (b % 2 == 1)return a * binaryPow(a, b - 1, m) % m;
	else {
		LL mul = binaryPow(a, b / 2, m);
		//注意此处必须以另一个变量来接收binaryPow()返回值，否则两次调用binaryPow()并未减少时间复杂度。
		return mul * mul % m;
	}
}

注意：1. 如果初始a可能大于m，则先对m取模

2. 如果m=1，则可以直接判断为0。

快速幂的迭代写法：

将b按二进制展开可以表示为b= $k_{n}k_{n-1}...k_{2}k_{1}k_{0}$ = $2^{k_{n}}+2^{k_{n-1}}+...+2^{k_2}+2^{k_1}+2^{k_0}$ 。所以可以将 $a^{b}$ 表示为 $a^{2^{k_n}+....2^{k_0}}$ ，迭代解法：

1. 如果b的第i位（第i次迭代，处理时是最低位）为1，则ans=ans*a%m。

2. a=a*a%m

3. b右移一位，相当于除2。

typedef long long LL;
//求a^b%m递归写法
LL binaryPow(LL a, LL b, LL m) {
	LL ans = 1;
	while (b>0) {
		if (b & 1 == 1) {     //该位为1说明需要累积。
			ans = ans * a % m;//令ans累积上a
		}
		a = a * a % m;
		b >>= 1;
	}
	return ans;
}

4.6 two pointers

4.6.2 归并排序

2-路归并排序的原理是：

将序列两两分组，将序列归并为 $\left \lceil n/2 \right \rceil$ 个组，组内单独排序；然后将这些组两两合并，生成 $\left \lceil n/4 \right \rceil$ 个组，组内单独排序；以此类推，直到只剩下一个组为止，归并排序的时间复杂度是O(nlogn)。

4.6.3 快速排序

快速排序的时间复杂度是O(nlogn)。

快速排序的原理：

1. 选定一个主元，将序列中不超过他的数放在他的左侧，比他大的数放在他的右侧；

2. 然后再分别从两侧的子序列中选择主元进行快速排序，直到调整区间不超过1。

当序列接近有序时会达到最坏的情况，时间复杂度为O(n^2)，随机选择主元能够将对于任意输入的时间复杂度降低到O(nlogn)。

Chapter 5 数学问题

5.2 最大公约数(gcd)和最小公倍数(lcm)

欧几里得算法：gcd(a,b)=gcd( b , a%b)。

lcm(a,b)=ab/d。(d=gcd(a,b))——a*b中d被乘了两次，除掉一个d则表示所有组成a，b的因子相乘。

5.4 素数

5.4.1 素数的判断

只需判断n能否被2,3,..., $\left \lfloor sqrt(n) \right \rfloor$ 整除即可。

5.4.2 素数表的获取

枚举法时间复杂度较高。

筛法能够有效降低时间复杂度O(nloglogn)。

算法从小到大枚举所有数，对每一个素数，筛去它的所有倍数，剩下的数即为素数。从2开始，如果验证到整数i，i还未被筛去，说明i就是一个素数（如果i是合数，必有小于i的质因子，而前期筛去素数的倍数时并没有筛掉i，说明i不是合数）。

利用筛法求解的时候注意：

1. 必须从2开始筛。

2. 素数表必须比n大1。

3. 注意函数中结束控制条件：验证的数9字i必须比设定的最大maxn（数组isPrime[maxn]）小，否则访问越界。

5.5 质因子分解

对一个正整数n来说，如果存在[2,n]的质因子，要么这些质因子都小于sqrt(n)；要么只存在一个大于sqrt(n)的质因子，其他质因子全小于等于sqrt(n)。

5.8 组合数

5.8.1 关于n!的问题

一、求n!有多少个质因子p

n!中有 $\left (\frac{n}{p}+\frac{n}{p^{2}}+\frac{n}{p^{3}}+... \right )$ 个质因子p，其中除法为向下取整。

n!中质因子p的个数，实际上等于1~n中p的倍数的个数n/p加上 $\frac{n}{p}!$ 中质因子p的个数。

推导过程：10！中2的个数

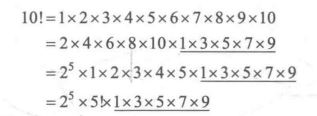
（10/2=5）+（5/2=2）+（2/2=1）=8个

5.8.2 组合数的计算

$C(n,m)=C_{n}^{m}=\frac{n!}{m!(n-m)!}$

一、计算 $C_{n}^{m}$ 的方法

1. 方法一：通过定义式暴力计算，但是由于阶乘一般比较大，所以即使是选择long long数据类型仍然很容易导致溢出。

2. 方法二：通过递推公式计算（最优方法）

$C_{n}^{m}=C_{n-1}^{m}+C_{n-1}^{m-1}$

递归边界： $C_{n}^{0}=C_{n}^{n}=1$

long long C(long long n, long long m) {
	if (m == n || m == 0)return 1;
	return C(n - 1, m) + C(n - 1, m - 1);
}

如果涉及到多次计算，为避免重复计算，可以用二维数组存储其值，也可以先将整张表都计算出来：

long long res[67][67] = { 0 };
//用一个数组记录已计算的C
long long C(long long n, long long m) {
	if (m == n || m == 0)return 1;
	if (res[n][m] != 0)return res[n][m];
	return res[n][m]=C(n - 1, m) + C(n - 1, m - 1);
}
//先将整张表计算出
const int n = 60;
void calC() {
	for (int i = 0; i <= n; i++) {
		res[i][0] = res[i][i] = 1;
	}
	for (int i = 2; i <= n; i++) {
		for (int j = 0; j <= i / 2; j++) {
			res[i][j] = res[i - 1][j] + res[i - 1][j - 1];
			res[i][i - j] = res[i][j];
		}
	}
}

3.方法三：通过定义式变形计算

因为运算过程涉及到乘除，所以一边乘一边除可以降低溢出的可能性。

二、计算 $C_{n}^{m}%p$ 的方法

1. 方法一：通过递推式计算

在5.8.2节C函数中修改即可，在返回时，返回 $\left ( C_{n-1}^{m}+C_{n-1}^{m-1}\right )%p$ 。

2. 方法二：根据定义式计算

$C_{n}^{m}%p=p_{1}^{c_1}\times p_2^{c_2}\times ...\times p_k^{c_k}%p$ ，可以通过快速幂来计算每一组 $p_i^{c_i}%p$ 。

遍历不超过n的所有素数 $p_i$ ，计算n!，m!，(n-m)!中分别含 $p_i$ 的个数x，y，z，可以知道 $C_{n}^{m}$ 中含有 $p_i$ 的个数x-y-z。

//使用筛法得到素数表prime，表中最大素数不小于n
int prime[maxn];

//计算C(n,m)%p
int C(int n, int m, int p) {
	int ans = 1;
	//遍历不超过n的左右质数
	for (int i = 0; prime[i] <= n; i++) {
		//计算C(n,m)中prime[i]的指数c，cal(n,k)为n！中含质因子k的个数
		int c = cal(n, prime[i]) - cal(m, prime[i]) - cal(n - m, prime[i]);
		//快速幂计算prime[i]^c%p
		ans = ans * binaryPow(prime[i], c, p) % p;
	}
	return ans;
}

Chapter 6 C++标准模板库（STL）

在STL提供容器中，绝大多数需要提供it，it2（it及it2为数组下标或者容器迭代器），实现的功能都是针对于[it, it2)之间的，即左闭右开！在使用时尤其注意右边界是否是需要作用it2指定的元素。如sort()、reverse();

6.1 vector

#include<vector>
using namespace std;
vector<typename> name;

typename可以是其他基本类型或STL容器，注意若typename也是STL容器需要在>>符号间加空格，如vector<vector<int> >name；可以将vector容器当做变长数组使用。

//一维已经固定的变长数组
vector<typename> Arrayname[arraySize]
//二维均可变长数组
vector<vector<int> > name;

访问方式：

（1）下标访问，同数组类似。

（2）迭代器访问：迭代器类似于指针。

vector<typename>::iterator it;

注意：在STL容器中，只有vector和string允许使用vi.begin()+k的形式。迭代器结束标志只能以it！=xxx结束，不支持大小比较。

vector常用函数：

push_back()在末尾添加元素。

pop_back()删除末尾元素。

insert(it,x)：在迭代器it处插入元素x。

erase(): 1）erase(it)删除it处元素。

2）erase(first,last)：删除[first,last)范围内的元素。

6.2 set

#include<set>
using namespace std;
set<typename> name;
set<typename>::iterator it;

set（集合）只能通过迭代器访问。

set中元素自动递增排序，且自动去除重复元素。

set常用函数：

find(value)返回set中对应值为value的迭代器。

erase(): 1）st.erase(it)删除it所指元素

st.erase(value)删除值为value的元素。

2）st.erase(first,last) 删除[first,last)的元素。

6.3 string

#include<string>
using namespace std;
string<typename> name;

注意：string头文件和string.h是不同的头文件。

通过下标访问和char数组相同。

注意：string类输出只能使用cout。要使用printf需要调用c_str();

string str;
......
cout << str;

printf("%s",str.c_str());

通过迭代器访问，string的迭代器定义方法略有不同：

string::iterator it;

string常用函数：

operator+=直接将两个string拼接。

compare operator：==,!=,<,<=,>,>=,比较的是字典序。

length()/size()均能返回string的长度。

insert()：1） insert(pos,string)在pos位置插入string。

2）insert(it,it2,it3)在it位置插入字符串（it2，t3为收尾迭代器），[it2,it3)。

erase()：1）str.erase(it)删除it所指字符。

2）str.erase(first,last)删除[first,last)区间字符。

str.erase(pos,length)删除从pos位置起length个字符。

substr():substr(pos,len)返回从pos位起长度为len的子串。

string::npos=-1作为find函数失配时返回值。

find(): str.find(str2)如果str2是str子串，返回第一次出现位置，失配返回string::npos；

str.find(str2,pos)从pos开始查找str2子串。

replace(): str.replace(pos,len,str2)把str从pos位开始长度为len的子串替换为str2.

str.replace(it1,it2,it3)把str的[it1,it2)替换为str2。

6.4 map

map可将任意基本类型（含STL容器）映射到任何基本类型（含STL容器）。

#include<map>
using namespace std;
map<typename1,typename2> mp;

typename1是键的类型，typename2是值的类型。

字符串到数组的映射，必须使用string。

通过下标访问mp[key]即可访问，因为map的键唯一。

通过迭代器访问

map<typename1,typename2>::iterator it;

map使用it->first访问键，it->second访问值。

map会按照键从小到大自动排序。

常用函数：

erase()：1） mp.erase(it)删除it所指键值对。

mp.erase(key)删除键key所表示的键值对。

2）mp.erase(first,last) 删除迭代器[first,last)所指键值对。

6.5 queue

queue只能通过front()访问队首元素，back()访问队尾元素。

使用pop()和front()需要用empty()判断队列是否为空。

6.6 priority_queue

#include<queue>
using namespace std;
priority_queue<typename> name;

只能通过top（）访问优先队列的队首元素。

优先队列按照优先级对队内元素自动排序，自动将优先级最高的元素排在top,不能使用front()、back()访问。

priority_queue内元素优先级设置：

（1）基本数据类型优先级设置：

priority_queue<int> q;
priority_queue<int,vector<int>,less<int> > q;

通过第一种方式定义，优先级：数值越大，优先级越高，或字典序越大，优先级越高。

第二种定义方式，vector<>,less<>中数据类型要与优先队列元素数据类型保持一致,

less<>表示数字越大，优先级越高；greater<>表示数字小的优先级高。

（优先队列的优先级设置与sort函数的比较函数相反）

（2）结构体的优先级设置

需要重载运算符<

struct fruit{
    string name;
    int price;
    friend bool operator < (fruit a,fruit b){
    return a.price < b.price;
    //表示价格高的优先级高。
    }
}

6.8 pair

使用pair需要添加utility头文件或者map头文件。

pair<typename1,typename2> p;

定义时初始化加上(元素1，元素2)即可

可以临时构建pair

pair<string,int>("haha",5)

make_pair("haha",5)

以p.first和p.second分别访问pair的两个元素。

比较操作数，先以first大小作为比较标准，当first相同时比较second。

用途：

代替二元结构体及其构造函数，

作为map的键值对来插入。

//功能一：简化二元结构体定义
struct _pair{
    typename1 first;
    typename2 second;
}
pair<typename1,typename2> p;

//功能二：用于map键值对插入
map<string,int> mp;
mp.insert(make_pair("haha",5));

6.9 algorithm头文件下常用函数

6.9.3 reverse()

reverse(it, it2)将数组指针在[it,it2)之间元素，或者容器的迭代器在[it,it2)范围内元素进行反转。对于本身有序的容器不可用。

6.9.4 next_permutation()

给出一个序列在全排列中的下一个序列，当next_permutation已经达到全排列的最后一个时会返回false，可用作循环结束条件！

6.9.5 fill()

fill()把数组或容器某一段区间赋某个相同值。注意同memset()不同：

memset只能按字节赋值，而fill()按照元素赋值，即fill赋值可以是数组类型对应范围内的任意值。

6.9.6 sort()

sort(首元素地址，尾元素地址的下一个地址，比较函数（选填）)

省略比较函数，默认对前面区间递增排序（char型数组默认按字典序）。

比较函数cmp的写法：

（1）基本数据类型数组排序

bool cmp(int a,int b){//或其他基本数据类型char double 
    return a<b;
    //表示按照递增顺序排列
    return a>b;
    //表示按照递减顺序排列
}

（2）结构体数组排序

bool cmp(结构名 a,结构名 b){
    return a.成员变量 > b.成员变量;
    //按照该成员变量递减排序
    return a.成员变量 < b.成员变量;
    //按照该成员变量递增排序
}

（3）其他容器排序：

仅有string、vector、deque允许排序。

6.9.7 lower_bound()和upper_bound()

lower_bound(first, last, val)寻找[first,last)范围内第一个≥val元素的位置，返回指针或者迭代器。即val值的下边界。

upper_bound(first, last, val)寻找[first,last)范围内第一个＞val元素的位置，返回指针或者迭代器。即val值的上边界。

Chapter 8 搜索专题

8.1 深度优先搜索（DFS）

深度优先搜索以“深度”作为关键词枚举所有完整路径。

DFS可以用模拟栈来实现，也可以使用递归实现，但递归也是通过系统栈来实现，本质上都是利用的栈的原理。

在每次分叉时，先将该分叉点入栈，再将子节点入栈，如果到达了死胡同，出栈，出栈检测是否还有其他子节点，如果有将另外的字节点入栈，反复进行上述操作，直到栈空为止。

递归中：递归式就是分叉口，递归边界就是死胡同。

剪枝：根据题目相关条件，当进行深度优先搜索时，如果到某个分叉口已经使得之后的节点都不能满足条件时，不再对该分叉口向下搜索了，可以降低无意义的运行时间。

深度优先搜索时需要标记节点是否已经访问过，否则会存在重复访问的问题。

8.2 广度优先搜索（BFS）

广度优先搜索以“广度”作为关键词，依次访问从该岔道口能够直接达到的所有节点。

广度优先搜索可以利用队列来实现。

从起点开始，对于每个分叉口，将所有支路节点依次进入队列，当这一层节点完全入队后，队首元素出队，从该元素继续向下广度优先搜索，直到达到死胡同。

广度优先搜索需要以是否进入过队列来作为标记，因为有可能还没访问该节点，该节点还在队列中，也会造成重复访问的问题。

对于STL的队列和栈来说，如果以结构为元素的话，入栈（入队）过程实际是创建了副本，如果需要修改原来的结构体内容，需要以指针作为元素。

Chapter 9 数据结构专题（2）

9.1 树与二叉树

9.1.1 树的定义与性质

树的性质：

1. 树可以没有结点，称为空树（root==NULL）。

2. 树的层次（layer）从根节点算起，根节点层次为1。

3. 结点的子树数量成为度（degree），树的度为最大的结点度。

4. 有n结点的树，边数一定是n-1；满足联通、边数=结点数-1的结构一定是树。

5. 叶节点的度为0，当树中只有一个节点（根节点）时，根节点也算作叶节点。

6. 结点深度：从根结点->该结点的深度值，树的深度=最大结点深度；

结点高度：最底层叶节点->该节点的高度值，树的高度=最大结点高度。

性质1和5常用作边界测试数据。

9.1.2 二叉树的递归定义

1. 要么二叉树没有结点，是空树；

2. 要么二叉树由根节点、左子树、右子树组成，且左右子树均为二叉树。

二叉树与度为2的树不同，二叉树严格区分左右子树。

两种特殊二叉树：

1. 满二叉树：每一层结点数都达到允许的最大结点数。

2. 完全二叉树：除最下面一层外，其余层的结点数都达到最大，且最底层只从左至右存在连续若干结点。

9.1.3 二叉树的存储结构和基本操作

存储结构：二叉链表。

基本操作中需要注意：

插入insert(node* &root,int x)必须使用引用，否则不能够正确插入。insert是根据条件插入，如果不满足条件会向下继续调用，如果不用引用，就不能把新产生的结点的指针赋给原来的二叉树的结点上。

完全二叉树可以使用数组存储，根据其特性。

对完全二叉树结点从上至下、从左至右依次编号（根节点编号为1），对于任意结点x，其左孩子一定是2x，右孩子一定是2x+1。

完全二叉树叶子结点个数为 $\left \lceil \frac{n}{2} \right \rceil$ 。

且数组存储的顺序正好是完全二叉树层序遍历的顺序。

9.2 二叉树的遍历

根据根节点访问的顺序：先序遍历，中序遍历，后序遍历（依靠DFS实现）

层序遍历（BFS实现）。

注意：层序遍历时，设置的队列，要以结点指针作为元素，否则不能实现对原树的修改。

只有中序遍历只能确定左右子树的结点，不能确定树的结构，必须有先序、后序、层序其一才能确定根节点。

如果要根据先序或者后序以及中序确定树，需要去寻找具体的关系，以下是根据先序和中序，确定递归调用的参数。

当前先序区间是[preL，preR],中序区间[inL，inR]。当前根节点：pre[preL]，in[k].左子树的结点数量为（k-inL）左子树的区间是：[preL+1,preL+k-inL]，[inL,k-1]。右子树的区间是：[preL+k-inL+1，preR]，[k+1，inR]。

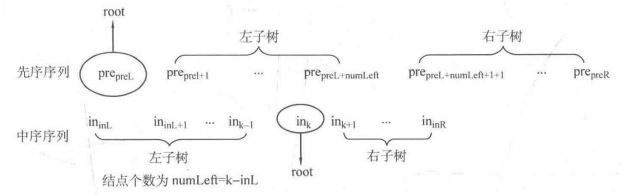
//当前先序区间为preL，preR；中序区间为inL，inR，重建二叉树,返回根节点地址
node* create(int preL, int preR, int inL, int inR){
	if (preL > preR) return NULL;
	node* root = new node;
	root->data = pre[preL];
	int k;
	for(int k = inL; k <= inR; k++){
		if (in[k] == pre[preL]) break;
	}
	root->lchild = create(preL + 1, preL + k - inL, inL, k - 1);
	root->rchild = create(preL + k - inL + 1, preR, k + 1, inR);
	return root;
}

9.2.5 二叉树的静态实现

静态二叉链表，左右指针域由int型代替（表示子节点在数组中的序号），二叉树以数组实现。

9.3 树的遍历

9.3.1 树的静态写法

以数组下标代替地址，子节点的地址需要用数组保存，或者采用vector容器，

struct node{
    typename data;// 数据域
    vector<int> child;//指针域
}

9.3.2 树的先根遍历

先访问根节点，再访问所有子树。

void PreOrder(int root) {
	;//访问当前节点
	for (int i = 0, i < Node[root].size(); i++) {
		PreOrder(Node[root].child[i]);
	}
}

对于叶节点，不会进入for循环，以此作为递归边界。

9.3.3 树的层序遍历

利用BFS原理即可实现。

9.3.4 从树的遍历看DFS和BFS

对于所有合法的DFS求解过程，可将分叉路口视作非叶节点，将死胡同视作叶节点，以此构造树的形式，树的先根遍历过程就是DFS遍历过程。

对所有合法的BFS求解过程，同样可以构造树，树的层序遍历就是BFS过程。

9.4 二叉查找树（BST）

9.4.1 二叉查找树的定义

1. 要么二叉查找树是一棵空树。

2. 要么二叉查找树由根节点、左子树、右子树组成，左子树和右子树都是二叉查找树，且满足：左子树结点数据域 ≤ 根节点数据域，右子树结点数据域＞根节点数据域。

9.4.2 二叉查找树的基本操作

一、查找

时间复杂度O(h)，h是树高。

二叉查找树的查找在于左右子树的选择，只需要在一条路径上查找，避免了在整棵树查找。

二、插入

二叉查找树的插入与查找类似，当在BST中查找x，而root为NULL时，说明查找失败，而在查找过程中可以确定，查找失败的地方就是应该插入的地方，所以在查找失败处插入新结点即可。

注意：同普通二叉树一样，BST的插入函数insert(node *&root, int x)必须使用引用，否则不能将新建结点正确链接到树上。

三、建立

依次将所有数据插入树即可。

四、删除

时间复杂度O(h)。

前驱：BST中比结点权值小的最大结点。左子树的最右孩子。

后继：BST中比结点权值大的最小结点。右子树的最左孩子。

删除操作：

1. root为NULL，结点不存在，直接返回。

2. 删除部分（比较搜索部分不作说明）：

root不存在左、右孩子则为叶节点，直接删除，将root直接设置为NULL，父节点就引用不到他了。

root存在左孩子，在左子树中查找前驱pre，让pre的数据覆盖root，删除pre。

root存在右孩子，在右子树中查找后继next，让next数据覆盖root，删除next。

注意：deleteNode(node* &root, int x)函数仍然需要使用引用。

可以将删除pre和next进行优化，以pre的左子树作为pre的父节点的右子树，释放pre的空间；以next的右子树作为next父节点的左子树，释放next的空间，以此优化空间使用。

9.4.3 二叉查找树的性质

对二叉查找树中序遍历，遍历结果有序。

9.5 平衡二叉树（AVL）

9.5.1 平衡二叉树的定义

平衡因子：左子树的高度 — 右子树的高度。

AVL树：仍是一棵二叉查找树，只是对AVL树任意结点，平衡因子的绝对值 ≤1。

AVL树可以使树的高度在插入元素后仍能够保持O(logn)级别。

对于任意结点root，root的height=max(左子树height，右子树height)+1

9.5.2 平衡二叉树的基本操作

二、插入

1. 左旋

B的左子树->A的右子树

A->B的左子树

B->root

void L(Node* &root) {
	Node* temp = root->rchild;
	root->rchild = temp->lchild;
	temp->lchild = root;
	updateHeight(root);
	updateHeight(temp);
	root = temp;
}

2. 右旋

A的右子树->B的左子树

B->A的左子树

A->root

void R(Node*& root) {
	Node* temp = root->lchild;
	root->lchild = temp->rchild;
	temp->rchild = root;
	updateHeight(root);
	updateHeight(temp);
	root = temp;
}

注意：左旋和右旋过程中，修改root之前，更新结点高度时，必须先更新两者中作为子节点（root）的高度，否则在后续高度更新过程中会产生错误。

3. 插入操作

只要将最靠近插入结点的失衡结点调整到正常，路径上所有节点都会正常。

四种失衡情况：第一个字母表示root左/右高度高，第二个字母表示root高的字节点的左右侧高度情况。

LL型：右旋（root）

LR型：左旋（root->lchild）,右旋（root）

RR型：左旋（root）

RL型：右旋（root->rchild），左旋（root）

void insert(Node*& root, int data) {
	if (root == NULL) {
		root = new Node;
		root->data = data;
		return;
	}
	if (data < root->data) {
		insert(root->lchild, data);
		updateHeight(root);//递归调用插入后，会更新该路径上所有节点的高度
		if (getBanlanceFactor(root) == 2) {
			if (getBanlanceFactor(root->lchild) == 1)R(root);
			else if (getBanlanceFactor(root->lchild) == -1) {
				L(root->lchild);
				R(root);
			}
		}
	}
	else {
		insert(root->rchild, data);
		updateHeight(root);
		if (getBanlanceFactor(root) == -2) {
			if (getBanlanceFactor(root->rchild) == -1)L(root);
			else if (getBanlanceFactor(root->rchild) == 1) {
				R(root->rchild);
				L(root);
			}
		}
	}
}

注意查看注释如何更新结点高度。

9.6 并查集

9.6.1 并查集的定义

并查集支持：合并两个集合，查找：判断两个元素是否在同一集合中。

用数组表示集合father[N]，father[i]表示元素i的父节点，如果father[i]==i，元素i是集合的根节点。同一个集合只有一个根节点，将其作为所属集合标识。

9.6.2 并查集的基本操作

一、初始化

令所有father[i]=i

二、查找

反复查找，直到满足father[i]==i。可以修改代码，在查找过程中将所有属于同一集合的结点的father[x]赋值为根节点（实现方式见9.6.3 路径压缩）。

三、合并

1. 判断是否属于同一个集合

2. 不属于同一集合之后合并，合并过程中，将一个集合的根节点的父亲指向另一个集合的根节点。

void Union(int a, int b){
    int faA = findFather(a);
    int faB = findFather(b);
    if(faA != faB){
        father[faA] = faB;
    }
}

9.6.3 路径压缩

修改findFather()函数，将当前查询结点路径上所有节点的父亲都指向根节点。

int findFather(int x) {
    int a = x;//保存查询起点
    while(x != father[x]){
        x=father[x];
    }//寻找根节点
    while(a != father[a]){
        int z = a;
        a = father[a];
        father[z] = x;
    }//将从查询起点起的路径上所有的结点的父亲修改为根节点
    return x;
}

9.7 堆

9.7.1 堆的定义与基本操作

一、堆的定义：堆是一个完全二叉树。

大顶堆：每个结点的值 ≥孩子结点的值。每个结点的值都是以其为根节点的子树的最大值。

小顶堆：每个结点的值≤孩子结点的值。每个结点的值都是以其为根节点的子树的最小值。

下列操作以大顶堆为例：

二、堆的初始化：先根据输入顺序，建立完全二叉树，再“从下往上，从右往左”进行向下调整。

向下调整：将当前节点V与左（L）右（R）孩子比较，假如孩子中存在比V大的，交换V和较大孩子的权值；交换完毕后，再次比较，直到V比孩子的权值都大，或V不存在孩子。

时间复杂度为O(logn)

//对heap数组在[low,high]区间向下调整，
//low为欲调整数组下标，high一般为最后一个元素数组下标
void downAdjust(int low, int high) {
    int i = low, j = i * 2;
    while(j <= high) {//存在孩子结点
        if(j + 1 <= high && heap[j + 1] > heap[j]){
            j = i + 1;
        }//j保存权值最大的孩子结点
        if(heap[j] > heap[i]) {
            swap(heap[j], heap[i]);
            i = j;
            j = 2 * i;
        }//如果较大权值孩子结点比当前节点大，当前节点向下调整。
        else{
        break;//孩子结点都比当前节点小，调整结束。
        }
    }
}

建堆就只需要对非叶节点进行向下调整，所以 i 从 $\left \lfloor \frac{n}{2} \right \rfloor$ 倒着枚举到1，在[i，n]的范围进行调整。

三、删除结点：

删除堆顶元素：以最后一个元素覆盖堆顶元素，然后对根节点进行向下调整。

四、添加元素：

添加元素：将欲添加元素放在数组最后，然后向上调整：

把欲调整元素与父元素比较，如果比父元素大，交换父元素和欲调整元素。直到到达堆顶或者权值比父节点小为止。

时间复杂度为O(logn)。

向上调整代码：

//对heap数组在[low,high]区间向上调整，
//low一般为1，high表示欲调整元素
void upAdjust(int low, int high) {
    int i = high, j = i / 2;
    while(j >= low) {
        if(heap[j] < heap[i]) {
            sawp(heap[j], heap[i]);
            i = j;
            j = i / 2;
        }
        else{
        break;
        }
    }
}

添加元素代码：

void insert(int x) {
    heap[++n] = x;
    upAdjust(1, n);
}

9.7.2 堆排序

堆排序取出堆顶元素，将堆的最后一个元素替换至堆顶，再将堆顶元素向下调整，重复上述操作，直到只剩一个元素。

倒着遍历数组，假设访问 i 号位，将堆顶元素与 i 号位元素交换，在[1,i-1]对堆顶元素向下调整。

void heapSort( ) {
    createHeap();//如果已经有堆了就不需要建堆操作
    for(int i = n; i > 1; i--) {
        swap(heap[1], heap[i]);
        downAdjust(1, i - 1);
    }
}

9.8 哈夫曼树

9.8.1 哈夫曼树

叶节点的带权路径长度 = 叶节点权值 x 路径长度

树的带权路径长度 = $\sum$ 叶节点带权路径长度

哈夫曼树的建立：

将初始状态下n个结点视作n棵树，合并根节点权值最小的两棵树，生成两棵树根节点的父节点，权值为二者之和，再将n-1棵树进行上述操作，直到只剩一棵树为止。

可以用优先队列实现建立哈夫曼树，下列代码是求哈夫曼树的带权路径长度：

#include<cstdio>
#include<queue>
#include<vector>
using namespace std;

priority_queue<long long, vector<long long>, greater<long long>> q;//代表小顶堆的优先队列

int main() {
    int n;
    long long temp, x, y, ans = 0;
    scanf("%d",&n);
    for(int i = 0; i < n; i++) {
        scanf("%lld", &temp);
        q.push(temp);
    }
    while(q.size() > 1) {
        x = q.top();
        q.pop();
        y = q.top();
        q.pop();
        q.push(x + y);
        ans += x + y;
    }
    printf("%d",ans);
    return 0;
}

Chapter 10 图算法专题

10.2 图的存储

一、邻接矩阵法：

设图G有N个结点，令二维数组G[N][N]表示图，G[i][j]为0表示顶点 i 和顶点 j 之间没有边，如果为k，则说明 i 和 j 之间有一条权为k的边。

读入邻接矩阵时，对于无向图，一定要保证G(i,j)=G(j,i)，否则在后续处理过程中会产生错误。

二、邻接表法：

把同一个顶点所有出边放在同一个列表中，N个结点就会有N个列表，这N个列表即为图G的邻接表。

如果邻接表只存储终点编号，不存放边权，则这N个列表为int型vector即可。

如果邻接表需要存储边权，则N个列表用Node型vector。

//不存储边权
vector<int>Adj[N]
//需要存储边权
struct Node {
    int v;//顶点编号
    int w;//边权
}
vector<Node>Adj[N]

10.3 图的遍历

10.3.1 深度优先搜索（DFS）遍历图

连通分量：无向图中，两点之间可互相到达，则两顶点连通，如果无向图G(V,E)任意两点均连通，则称G为连通图。

强连通分量：有向图中，两顶点之间能够互相到达（注意方向），则两顶点强连通，如果有向图G(V,E）任意两点均互相强连通，则称G为强连通图。

对图的DFS遍历就是对这个图所有的连通块（连通分量或强连通分量）分别遍历。

DFS遍历图的基本思想是：将经过的顶点设置为已访问，在下一次递归碰到这个顶点不做处理，直到整个图的顶点都被标记为已访问。

DFS遍历图的伪代码：

DFS (u) {
    vis[u] = true;
    for(从u出发所有能够到达的顶点v)//枚举从u出发的所有节点，深度优先
        if (vis[v] == false) DFS(v);//如果v未被访问，访问之
}

DFSTrave(G) {
    for(G的所有顶点u) {
        if(vis[u] == false) {
            DFS(u);//确保每个连通块都能被完全访问。
        }    
    }
}

10.3.2 广度优先搜索（BFS）遍历图

BFS遍历图的基本思想是：建立一个队列，把初始顶点加入队列中，此后每次都去队首顶点进行访问，并把从该顶点出发可到达的未曾加入过队列的顶点全部加入队列，直到队列为空。

BFS遍历图的伪代码：

BFS(u) {
    queue q;
    将u加入队列；
    inq[u] = true;
    while(q非空) {
        取q的队首元素u访问；
        for(所有能从u到达的顶点v) {
            if (inq[v] == false){
                将v入队;
                inq[v] = true;
            }
        }
    }
}

BFSTrave(G) {
    for(G所有顶点u) {
        if(inq[u] == false) {
            BFS(u);
        }
    }
}

10.4 最短路径

10.4.1 Dijkstra算法

Dijkstra算法用于解决单源最短路问题（从同一点出发，到图中各点路径最短）。

Dijkstra算法思想：对图G(V,E)社指集合S，存放已经访问的顶点，然后从集合V-S中选择与起点s的最短距离最小的顶点记为u，访问并加入集合S，之后令顶点u为中介点，优化起点s与所有可以经过u到达的点v之间的最短距离。

Dijkstra算法伪代码：

Dijkstra(G, d[], s) {
    初始化;
    for(循环n次) {
        u = 使d[u]最小的还未被访问的顶点的标号;
        记u已被访问;
        for(从u出发能到达的所有顶点v) {
            if(v未被访问 && 以u为中介点使s到顶点v的最短距离d[v]更优) {
                优化d[v];
            }
        }
    }
}

注意：Dijkstra算法只能解决所有边权都是非负数的情况。

如果需要输出最短路径，可以在Dijkstra算法 if（.....）优化 d[v] 处增加将u赋给pre[v]的操作，如此，pre数组就可记录各点的前驱，输出s到v最短路径时，就从pre[v]开始递归，直到到达s点。

针对题目，Dijkstra算法可以做的优化（这些优化都只在优化d[v]的步骤进行优化）：

以邻接矩阵法为例：

1. 给每条边增加边权，要求最短路径有多条时，输出该边权之和最小（或最大）。

增加 cost[u][v] 表示从u到v的边权，用c[u]表示从s到u的边权之和。初始化时 c[s]=0；其他都设置为INF。

如果对于中介点u，d[v]不变，但是边权之和能够减小时，优化c[v]。

for (int v = 0; v < n; v++) {
    //如果v未访问，且u能到达v
    if（vis[v] == false && G[u][v] !=INF） {
        if(d[u] + G[u][v] < d[v]) {
            d[v] = d[u] + G[u][v];
            c[v] = c[u] + cost[u][v];
        }
        else if(d[u] + G[u][v] == d[v] && c[u] + cost[u][v] < c[v]) {
             c[v] = c[u] + cost[u][v];
        }
    }    
}

2. 给每点增加点权，要求最短路径有多条时，输出点权和最大（或最小）。

以 weight[u] 表示点 u 的点权，w[u] 表示从 s 到 u 的点权之和。初始化时 w[s] = weight[s],其他点都为0。

如果对于中介点u，d[v]不变，但是点权之和能够增大时，优化c[v]。

for (int v = 0; v < n; v++) {
    //如果v未访问，且u能到达v
    if（vis[v] == false && G[u][v] !=INF） {
        if(d[u] + G[u][v] < d[v]) {
            d[v] = d[u] + G[u][v];
            w[v] = w[u] + weight[v];
        }
        else if(d[u] + G[u][v] == d[v] && w[u] + weight[v] > w[v]) {
             w[v] = w[u] + weight[v];
        }
    }    
}

3. 直接问最短路径条数。

增加数组num[]，num[u] 表示 s 到 u 的最短路径数。

如果从中介点 u 能让 v 简化，则到 v 的最短路径数与 u 相同；如果正好相等，说明到 v 能够增加 num[u] 条最短路径。

for (int v = 0; v < n; v++) {
    //如果v未访问，且u能到达v
    if（vis[v] == false && G[u][v] !=INF） {
        if(d[u] + G[u][v] < d[v]) {
            d[v] = d[u] + G[u][v];
            num[v] = num[u];
        }
        else if(d[u] + G[u][v] == d[v]) {
            num[v] += num[u];
        }
    }    
}

使用Dijkstra算法记录所有最短路径。

因为需要记录所有最短路径，每个结点会存在多个前驱结点，所以用vector<int> pre[maxn]记录前驱结点，对于每个结点 v，pre[v] 是一个变长数组，可以存放节点v所有能产生最短路径的前驱结点。修改之后的代码：

for (int v = 0; v < n; v++) {
    //如果v未访问，且u能到达v
    if（vis[v] == false && G[u][v] !=INF） {
        if(d[u] + G[u][v] < d[v]) {
            d[v] = d[u] + G[u][v];
            pre[v].clear();
            pre[v].push_back(u);    
        }
        else if(d[u] + G[u][v] == d[v]) {
            pre[v].push_back(u);
        }
    }    
}

之后可以利用DFS获取所有最短路径。

根据pre数组可以生成一棵递归树，每次从根节点到达叶子结点可以得到一条完整的最短路径。计算第二标尺的值，可以选择得到题目需要的解。

int optvalue;//第二标尺最优值
vector<int> pre[maxn];
vector<int> path,tempPath;//最优路径，临时路径
void DFS(int v) {
    if(v == s) {
        tempPath.push_back(v);
        int value;
        计算路径tempPath上的value值;
        if(value 优于 optvalue) {
            optvalue = value;
            path = tempPath;
        }
        tempPath.pop_back();
        return;
    }
    tempPath.push_back(v);
    for(int i = 0; i < pre[v].size(); i++) {
        DFS(pre[v][i]);
    }
    tempPath.pop_back();
}

10.4.2 Bellman-Ford算法和SPFA算法

10.4.3 Floyd算法

Floyd算法解决全源最短路问题，求图G(V,E)中任意两点 u，v 之间的最短路径，时间复杂度为O(n^3)。

Floyd算法伪代码：

枚举顶点k ∈[1,n]
    以顶点k作为中间结点，枚举所有对i和j（i∈[1,n]，j∈[1,n]）
        如果dis[i][k] + dis[k][j] < dis[i][j]成立
            dis[i][j] = dis[i][k] + dis[k][j];

10.5 最小生成树

10.5.1 最小生成树及其性质

最小生成树：在无向图G(V,E)中求一棵树T，T含有G所有顶点，且所有边来自G，并且满足整棵树的边权之和最小。

最小生成树的性质：

1. 最小生成树，边数=顶点数-1，且不存在环。

2. 对于给定图G，最小生成树可能不唯一，但是边权之和一定唯一。

3. 最小生成树在无向图G中生成，根节点可以是任意结点。

Prim算法和Kruskal算法都采用贪心思想，可用于求最小生成树。

10.5.2 Prim算法

基本思想：设置集合 S，存放已经访问的顶点，每次从集合 V-S 中选取与集合 S 的最短距离最小的一个顶点 u，访问并加入 S；以 u 为中介点，优化所有从 u 能够到达的顶点 v 与集合 S 之间最短距离，重复上述 n 次操作。

Prim算法：优化顶点 v 到集合 S 的最短距离；

Dijkstra算法：优化顶点 v 到起点 s 的最短距离。

具体实现：

1. 集合 S 的实现：用一个bool型数组 vis[] 表示顶点是否已经访问，true表示已访问，false表示未访问。

2. 与集合S的最短距离：用int型数组 d[] 存放顶点 Vi 与集合 S 的最短距离，初始时，只有起点s的d[s]赋值为0，其余顶点都赋一个很大的数INF。

伪代码：

//G为图，一般设置为全局变量，数组d为顶点到集合S的最短距离
Prim （G，d[]） {
    初始化；
    for（循环n次） {
        u=使d[u]最小的还未被访问的顶点；
        记u已经访问；
        for（从u出发能够到达的所有顶点v） {
            if（v未被访问&&以u为中介使得v与集合S的最短距离d[v]更优）{
                将G[u][v]赋值给v与集合S最短距离d[v]；
            }    
        }
    }
}

时间复杂度是O(V^2)，邻接表实现的prim算法可以通过堆优化使时间复杂度降低到O(VlogV+E)。prim 算法一般用于顶点数较少、边数较多的情况。

10.5.3 Kruskal算法

Kruskal算法采取边贪心的策略。

基本思想：每次选择最小边权的边，如果边的两个顶点不在同一个连通块，将这条边加入最小生成树。

1. 对所有边按照边权从小到大排序

2. 按边权从小到大测试所有边，如果当前边的两个顶点不在同一个连通块中，则把这条测试变加入当前最小生成树中；否则，丢弃。

3. 执行步骤2，直到最小生成树的边数等于总边数-1,或者测试完所有边时结束。当结束时，如果最小生成树的边数小于总顶点数-1，则该图不连通。

Kruskal算法用一个结构体保存边，（顶点u，v；边权cost）

伪代码：

int Kruskal（）{
    令最小生成树边权之和为ans，最小生成树的当前边数Num_Edge；
    将所有边按权从小到大排序；
    for（从小到大枚举所有边） {
        if（当前测试边的两个端点在不同的连通块中）{
            将该测试边加入最小生成树；
            ans += 测试边边权；
            Num_Edge++；
            当边数Num_Edge等于顶点数-1时结束循环；
        }
    }
    return ans；
}

判断测试边两个端点是否在同一连通块、将测试边加入最小生成树，需要使用到并查集。

Kruskal算法的时间复杂度是O(ElogE)。

10.6 拓扑排序

10.6.2 拓扑排序

拓扑排序是将有向无环图（DAG）G的所有顶点排成一个线性序列（拓扑序列），使得对图G中任意两个顶点 u，v ，如果存在边 u->v，则在序列中 u 一定在 v 前面。

基本思想：

1. 定义一个队列，将所有入度为0的结点加入队列

2. 取队首顶点，输出。删除所有从他出发的边（可以不删去），并将这些边到达的顶点的入度减1，如果某个结点的入度减为0，将其入队。

3. 反复进行第2步，直到队列为空。如果队列为空时如果队的节点数目恰好为N，则拓扑排序成功，G为有向无环图，否则，拓扑排序失败，G中有环。

10.7 关键路径

10.7.1 AOV网和AOE网

AOV网：顶点活动网，用顶点表示活动，边表示活动间优先关系的有向图。

AOE网：边活动网，以带权边集表示活动，用顶点表示事件的有向图。边权表示活动需要时间。事件：前面的活动已经结束。

AOV网和AOE网都不应该有环。

AOE网中最长路径就是关键路径，关键路径上的活动是关键活动。

关键路径总是选择最长道路，也是完成所有活动的最短时间。

10.7.2 最长路径

对于没有正环的图，要求最长路径，将所有边权乘以-1，使用Bellman-Ford算法或者SPFA算法求最短路径长度，将结果取反即可得到。

如果图中有正环，最长路径不存在。

10.7.3 关键路径

设置数组 e 和 l ，其中 e[r] 和 l[r] 表示活动ar的最早开始时间和最晚开始时间。

设置数组 ve 和 vl ，其中 ve[i] 和 vl[i] 分别表示事件 i 的最早发生时间和最迟发生时间。

对于活动ar，Vi最早发生时ar立刻进行，则ar发生时间最早，e[r]=ve[i] ；

如果 l[r] 是ar最迟发生时间，那么 l[r] + lenght[r] 就是事件 Vj 的最迟发生时间，所以 l[r]=vl[j]-legnth[r]；

假设Vj可以由 Vi1~Vik达到，那么 $ve[j]=\underset{p}{max}\left \{ ve[ip]+length[rp] \right \}$

如果要获得 ve[j] 的正确的值，那么ve[i1]~ve[ik]必须已经得到，即在访问某结点时，其前驱结点都已经访问完毕，拓扑排序可以实现。

修改后拓扑排序代码：

stack<int> topOrder;
bool topologicalSort() {
    queue<int> q;
    for(int i = 0; i < n; i++) {
        if(inDegree[i] == 0) {
            q.push(i);
        }
    }
    while(!q.empty()) {
        int u = q.front();
        q.pop();
        topOrder.push(u);
        for(int i = 0; i < G[u].size(); i++) {
            int v = G[u][i].v;
            inDegree[v]--;
            if(inDegree[v] == 0) [
                q.push(v);
            }
            //用ve[u]来更新u的所有后继结点v
            if(ve[u] + G[u][i].w > ve[v] ) {
                ve[v] = ve[u] +G[u][i].w;
            }
        } 
    
    }
    if(topOrder.size() == n) return true;
    else return false;
}

假设 Vi 能够达到 Vj1 ~Vjk,那么 $vl[i]=\underset{p}{min}\left \{ vl[jp]-length[rp] \right \}$

如果要获得 vl[i] 的正确的值，那么vl[j1]~vl[jk]必须已经得到，即在访问某结点时，其后继结点都已经访问完毕，逆拓扑排序可以实现。上述代码中topOrder栈出栈即是逆拓扑序列。

fill（v1, v1 +n , ve[n-1] ）;
while(!topOrder.empty()) {
    int u = topOrder.top();
    topOrder.pop();
    for(int i = 0; i < G[u].size(); i++) {
        int v = G[u][i].v;
        //用u的所有后继结点v的vl值来更新Vl[u]
        if(vl[v] - G[u][i].w <vl[u]) {
            vl[u] = vl[v] - G[u][i].w;
        }
    }
}

总结：

1. 拓扑排序和你拓扑排序获得各顶点的最早发生时间和最晚发生时间
最早（拓扑）： $ve[j]=\underset{i,\exists i->j}{max}\left \{ ve[i]+length[i->j] \right \}$

最迟（逆拓扑）： $vl[i]=\underset{j,\exists i->j}{min}\left \{ vl[j]-length[i->j] \right \}$

2. 用上边结果计算各边最早开始时间和最晚开始时间

最早：e[i->j] = ve[i]

最晚：l[i->j] = vl[j] - length[i->j]

3. e[i->j] = l[i->j] 的活动即为关键活动。

Chapter 11 动态规划专题

11.1 动态规划的递归写法和递推写法

11.1.1 动态规划

最优化问题：动态规划将一个复杂问题分解为多个子问题，通过综合子问题的最优解来得到原问题的解。

最优子结构：一个问题的最优解能够通过子问题的最优解求出。

必须拥有重叠子问题和最优子结构才能通过动态规划解决。

递归写法也叫作记忆化搜索。

11.1.2 动态规划的递归写法

记忆化搜索：记录子问题的解，避免下次遇到相同子问题（重叠子问题）时重复计算。

递归写法是从顶向下，分解问题，直到分解到边界。

11.1.3 动态规划的递推写法

数塔问题：以二维数组 f[N][N] 存储每一层的数字，令 dp[i][j] 表示从第 i 行第 j 个数字到最底层路径能够得到的最大和。

要求得 dp[i][j] 就必须求得 dp[i+1][j] 和 dp[i+1][j+1] 中的最大值，由此可以得状态转移方程：

$dp[i][j]=max(dp[i+1][j], dp[i+1][j+1]) + f[i][j]$

递推边界：

$dp[n][i]=f[n][i](1\leqslant i\leqslant n)$

//递推部分代码
for (int i = n - 1; i >= 1; i--) {
    for(int j = 1; j <= i; j++) {
        dp[i][j] = max( dp[i+1][j], dp[i+1][j+1]) + f[i][j];
    }
}

递推写法是自底向上，从边界开始向上求解问题。

分治和动态规划的区别：

分治法分解出的问题是不重叠的，动态规划求解的问题拥有重叠子问题。

分治法求解的不一定是最优解问题，动态规划求解的是最优解问题。

贪心和动态规划的区别：

贪心自顶向下解决问题，通过一种策略直接选择一种子问题求解，其他子问题放弃求解。

动态规划自底向上求解问题，每一种子问题都被求解了，最终选择最优的解。

11.2 最大连续子序列和

        令状态 dp[i] 表示以 A[i] 作为结尾的连续序列的最大和，求解整个序列的最大连续子序列和就是求数组 dp 中的最大值。
        对于 dp[i] 只有两种情况：
                1.最大和的连续序列只有一个元素，以 A[i] 开头，以 A[i] 结尾。
                2.最大和的连续序列有多个元素，从某处 A[p]开始，A[i] 结尾。

状态转移方程：

$dp[i]=max(A[i],dp[i-1]+A[i])$