图像处理(HSV) – 源码巴士

**1.图像相似性计算

HSV模型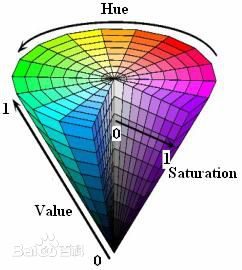
在这里插入图片描述
HSV颜色检测：https://www.jianshu.com/p/33af63a63a12
①色调H（Hue）
用角度度量，取值范围为0°～360°，从红色开始按逆时针方向计算，红色为0°，绿色为120°,蓝色为240°，。它们的补色是：黄色为60°，青色为180°,品红为300°，0°- 359°时颜色会依次变换当角度到达360°时也就是红色，角度也就又回到0°了，所以总共为360°，每变换1°时，色相就会有轻微的变化！如果是顺时针的话这个变换过程会从红色逐渐变换到绿色，在由绿色逐渐变换到蓝色，在由蓝色逐渐变换到红色！逆时针的话就是相反的！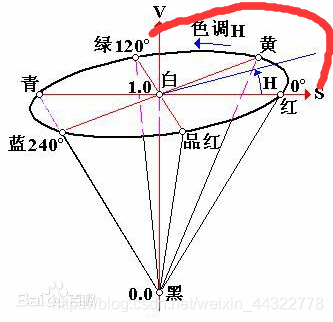
在这里插入图片描述
②饱和度 S（Saturation）
饱和度S表示颜色接近光谱色的程度。一种颜色，可以看成是某种光谱色与白色混合的结果。其中光谱色所占的比例愈大，颜色接近光谱色的程度就愈高，颜色的饱和度也就愈高。饱和度高，颜色则深而艳。光谱色的白光成分为0，饱和度达到最高。通常取值范围为0%～100%，值越大，颜色越饱和。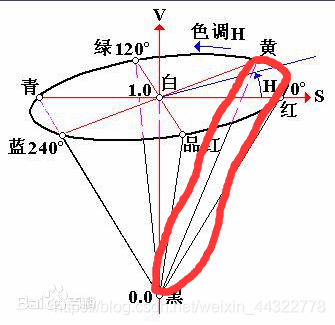
在这里插入图片描述
③明度V（Value）
明度表示颜色明亮的程度，对于光源色，明度值与发光体的光亮度有关；通常取值范围为0%（黑）到100%（白）。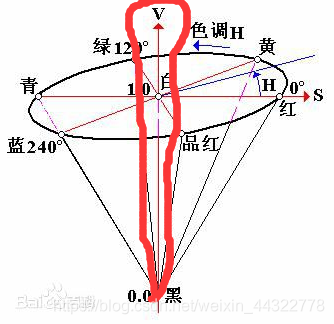

————————————————
原文链接：https://blog.csdn.net/bjbz_cxy/article/details/79701006
step1：RGB颜色空间到HSV颜色空间的转换**

import math
import cv2  
import numpy as np  
from matplotlib import pyplot as plt
import matplotlib.mlab as mlab  

img = cv2.imread('~/target1.jpg',cv2.IMREAD_COLOR)
HSV = cv2.cvtColor(img, cv2.COLOR_BGR2HSV)

step2：多维矩阵转换为向量数组
第一步我们将RGB颜色空间转换为HSV后得到的是多维的矩阵格式。而在python中，无论是画直方图还是接下来我们需要使用的欧几里得距离计算都需要向量表示。因此，在这一步我们需要对第一步获得结果进行处理，最终的表示结果是向量格式。

H, S, V = cv2.split(HSV)
aH = np.array(H).flatten()
aS = np.array(S1).flatten()
aV = np.array(V).flatten()

step3:HSV三维空间坐标计算公式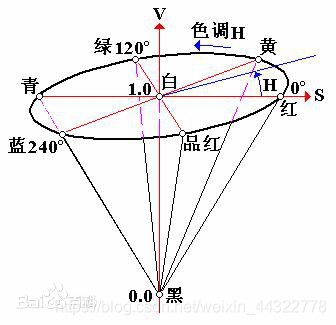
在这里插入图片描述
在斜边长R，底面圆半径为r，高为h的HSV圆锥体内，以地面圆心为原点，H=0为x轴正方向建立坐标轴。那么色值是(H,S,V)的点的三维坐标(x,y,z)是

x=r∗V∗S∗cosH
y=r∗V∗S∗sinH
z=h∗(1−V)

x1 = r * V1[i] * S1[i] * math.cos(H1[i] / 180.0 * math.pi);
y1 = r * V1[i] * S1[i] * math.sin(H1[i] / 180.0 * math.pi);
z1 = h * (1 - V1[i]);

完整代码：

import math
import cv2  
import numpy as np  
from matplotlib import pyplot as plt
import matplotlib.mlab as mlab  

img1 = cv2.imread('/home/*/result/target1.jpg',cv2.IMREAD_COLOR)

HSV1 = cv2.cvtColor(img1, cv2.COLOR_BGR2HSV)
aH1, aS1, aV1 = cv2.split(HSV1)
H1 = np.array(aH1).flatten()
S1 = np.array(aS1).flatten()
V1 = np.array(aV1).flatten()

# img2 = cv2.imread('/home/*/allAreaColor/result1.jpg',cv2.IMREAD_COLOR)
img2 = cv2.imread('/home/*/localColor/result1.jpg',cv2.IMREAD_COLOR)

HSV2 = cv2.cvtColor(img2, cv2.COLOR_BGR2HSV)
aH2, aS2, aV2 = cv2.split(HSV2)
H2 = np.array(aH2).flatten()
S2 = np.array(aS2).flatten()
V2 = np.array(aV2).flatten()

R = 100.0;
angle = 30.0;
h = R * math.cos(angle / 180 * math.pi);
r = R * math.sin(angle / 180 * math.pi);

sum = 0.0
for i in range(0, len(H1)):
    x1 = r * V1[i] * S1[i] * math.cos(H1[i] / 180.0 * math.pi);
    y1 = r * V1[i] * S1[i] * math.sin(H1[i] / 180.0 * math.pi);
    z1 = h * (1 - V1[i]);

    x2 = r * V2[i] * S2[i] * math.cos(H2[i] / 180.0 * math.pi);
    y2 = r * V2[i] * S2[i] * math.sin(H2[i] / 180.0 * math.pi);
    z2 = h * (1 - V2[i]);

    dx = x1 - x2;
    dy = y1 - y2;
    dz = z1 - z2;

    sum = sum + dx * dx + dy * dy + dz * dz

eucli_dean = math.sqrt(sum)
print eucli_dean

原文链接：https://blog.csdn.net/weixin_44322778/article/details/100006896