def levenshtein(first, second):
if len(first) > len(second): # 保证长度小的在后
first, second = second, first
if len(first) == 0: # 空字符替换成second
return len(second)
if len(second) == 0: # xxx 替换成空
return len(first)
first_length = len(first) + 1
second_length = len(second) + 1
"""因为在此初始化每行都是从0~ second_length, 需要判断两个字符串的长度,返回相应的编辑距离"""
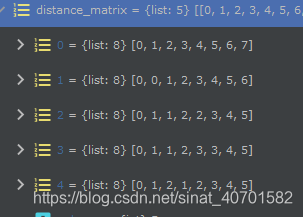
distance_matrix = [list(range(second_length)) for x in range(first_length)]
# print distance_matrix
for i in range(1, first_length):
for j in range(1, second_length):
deletion = distance_matrix[i - 1][j] + 1
insertion = distance_matrix[i][j - 1] + 1
substitution = distance_matrix[i - 1][j - 1]
if first[i - 1] != second[j - 1]:
substitution += 1
distance_matrix[i][j] = min(insertion, deletion, substitution)
print(distance_matrix[-1][-1])
return distance_matrix[-1][-1]
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
n1 = len(word1)
n2 = len(word2)
dp = [[0] * (n2 + 1) for _ in range(n1 + 1)]
# 第一行
for j in range(1, n2 + 1):
dp[0][j] = dp[0][j-1] + 1
# 第一列
for i in range(1, n1 + 1):
dp[i][0] = dp[i-1][0] + 1
for i in range(1, n1 + 1):
for j in range(1, n2 + 1):
if word1[i-1] == word2[j-1]:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = min(dp[i][j-1], dp[i-1][j], dp[i-1][j-1] ) + 1
print(dp)
return dp[-1][-1]
分析
(一)、当word1[i]==word2[j]时,由于遍历到了i和j,说明word1的0~ i-1和word2的0~ j-1的匹配结果已经生成<前n个位置都是相匹配的>,
由于当前两个字符相同,
因此无需做任何操作,dp[i][j]=dp[i-1][j-1]
(二)、当word1[i]!=word2[j]时,可以进行的操作有3个:
① 替换操作<0~ i/j -1两者的字符字符都相同>:
可能word1的0~ i-1位置与word2的0~ j-1位置的字符都相同,
只是当前位置的字符不匹配,进行替换操作后两者变得相同<其实没有真真正正做替换操作,只是在斜对角线的基础上增加一个操作>, 所以此时dp[i][j]=dp[i-1][j-1]+1(这个加1代表执行替换操作)
②删除操作<word1的长度大于word2的长度>:
若此时word1的0~ i-1位置与word2的0~ j位置已经匹配了, 此时多出了word1的i位置字符,应把它删除掉,才能使此时word1的0~ i(这个i是执行了删除操作后新的i)和word2的0~j位置匹配,因此此时dp[i][j]=dp[i-1][j]+1(这个加1代表执行删除操作)
③插入操作<word1的长度小于word2的长度>:
若此时word1的0~ i位置只是和word2的0 ~ j-1位置匹配, 此时只需要在原来的i位置后面插入一个和word2的j位置相同的字符使得此时的word1的0 ~ i(这个i是执行了插入操作后新的i)和word2的0~j匹配得上, 所以此时dp[i][j]=dp[i][j-1]+1(这个加1代表执行插入操作)
④由于题目所要求的是要最少的操作数:所以当word1[i] != word2[j] 时,
需要在这三个操作中选取一个最小的值赋格当前的dp[i][j]
(三)总结:状态方程为:
if(word1[i] == word2[j]):
dp[i][j] = dp[i-1][j-1]
else:
min(dp[i-1][j-1],
dp[i-1][j],
dp[i][j-1])+1 # 三种操作就看哪些操作最便宜
Q&A
- 斜对角线为啥代表替换?
答:斜对角线代表两个单词一 一对应位置的数据 - 让word1变成word2的模样如何做?
答:可以采用替换,删除<(i-1,j) j不变,i往上一格>,插入<(i,j-1) i不变, j 往前移动一格 NOTACK 不知道为啥这代表插入>的直角坐标系表示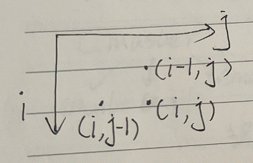
- 解法1 和解法2的输出区别
解法2输出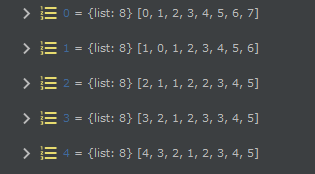
解法1 输出<刚开始初始化,每一行都是0~ 7>