前言

这篇文章我整理了力扣上一些难度偏低和适中的二分查找例题，整理了一些我对二分查找的浅见和方法，题解也仅是通俗讲解，并非代表最好，希望帮助 大家能够更好地理解二分查找。本人代码和见识有限，，有错误欢迎指出！

二分查找

二分查找也叫作折半查找法，每次查找一次便缩小一次范围，关键就在于边界问题和范围的缩小

第一题：二分查找

首先我们举一个比较经典的例子：力扣：二分查找

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

我们先随便举出一种情况：
题目变量：int search(int* nums, int numsSize, int target)

解题思路

1. 我们首先定义两个边界int left = 0，right = numsSize - 1，需要注意的是我所定义的right变量是最后一个元素的下标。

2. 关于循环部分：while(left < right)，因为我的左边界left和右边界right都是可以取到的下标（不会越界访问），当left = right的时候结束循环，如果按照这种方法写while(left <= right)的话，部分情况会出现死循环的情况

3. 然后再定义int mid = left + (right - left) / 2;，除了这个表达式之外，还有一个int mid = (left + right) / 2;其实这两个表达式的运算结果都是一样的，但是前者能够防止数据溢出的情况

4. 如果nums[mid]<target，那就说明mid在target的左边（题意数组是升序的），因为target不可能出现在[0,mid]的位置了，所以这时候我们就要调整左边界left的大小，让搜索范围更新成[mid+1,right] ，即left = mid +1;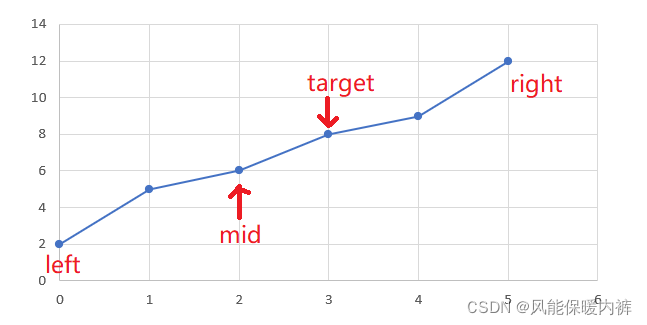

5. 如果nums[mid]>target，那就说明mid在target的右边，同理，这时候target就不可能出现在mid右边的位置了，所以我们就要调整右边界的大小，减少搜索范围，即right = mid - 1。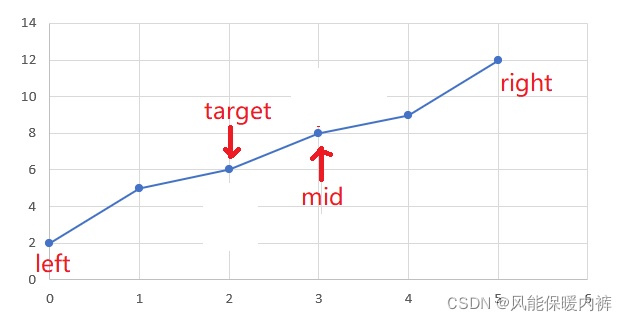

（为啥是mid-1? 因为nums[mid]已经大于target了，nums[mid]就肯定不等于target，mid就可以从我们的搜索范围中除去)

6. 然后重复3,4步骤即可，如果出现了等于的情况，那就不用想了，符合题意，直接返回这个坐标
7. 如果二分查找都结束了，也就是left = right 了，我们就要判断nums[left]是否为target，是的话，返回left，否则返回-1；

GIF

（假设target=7，在这个例子中应该返回-1）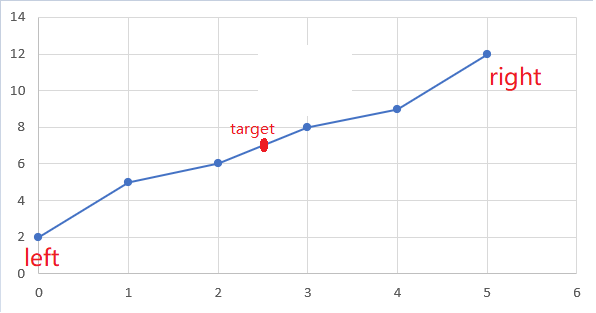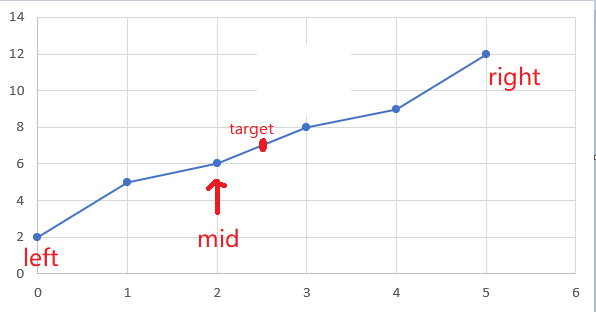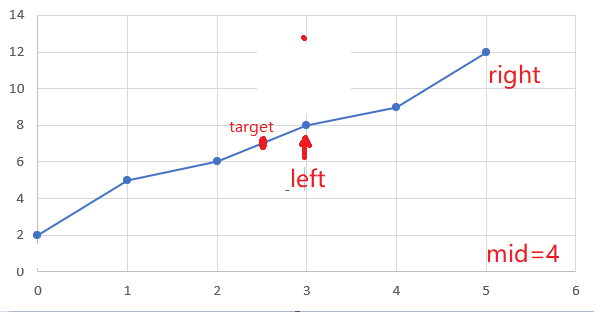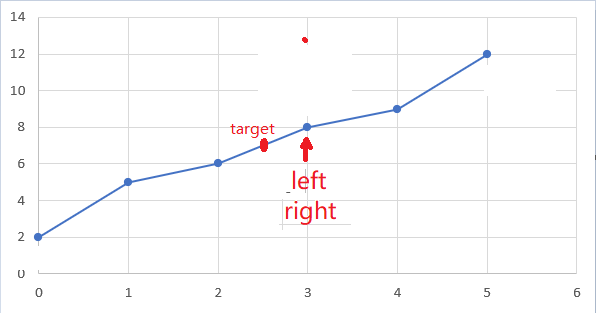

代码

int search(int* nums, int numsSize, int target)
{
    int left=0;
    int right=numsSize-1;
    while(left<right)
    {
        int mid=left+(right-left)/2; //防止溢出
        if(nums[mid]<target)
        {
            left=mid+1;
        }
        else if(nums[mid]>target)
        {
            right=mid-1;
        }
        else
        {
            return mid;
        }
    }
    return nums[left]==target?left:-1;//如果不等于说明不存在，返回-1
}

第二题：搜索插入位置

这个题难度就稍微上升了一丢丢：搜索插入位置

题目：给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

解题思路

所给函数体：int searchInsert(int* nums, int numsSize, int target)

1. 首先还是先定义int left = 0, right = numsSize - 1 ;和我的循环体模板while(left < right)
2. 如果nums[mid] < target，那说明插入位置肯定不是mid也不是小于mid的下标，所以我们要把mid以及mid左边的下标排出我们的搜索范围，即left = mid + 1;
3. 如果nums[mid] > target，那就说明插入位置肯定不在mid右边，但是，可不可以是mid呢？可以看出在下图这种情况的时候，target又刚好不是数组中的元素，此时插入位置恰好是mid，所以mid下标不能移出搜索范围，即更新：right = mid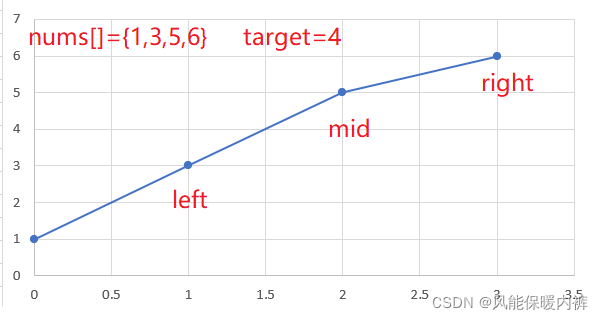
4. 然后按照2和3循环。如果nums[i] = target，那就容易了，直接返回
5. 但是！以我这种方法，当nums[] = {1,3,5,6} target = 7，也就是target比数组中元素都大的时候，二分查找结束的时候，下标left会等于3，但是这时候应该插入的位置应该是4才对，所以在这种情况下，我单独判断二分查找结束时，nums[left]会不会小于target就行啦，如果最后nums[left] < target，那就返回left+1

代码

int searchInsert(int* nums, int numsSize, int target)
{
    int right=numsSize-1,left=0;
    while(left<right)
    {
        int mid=left+(right-left)/2;
        if(nums[mid]<target) 
        {
            left=mid+1;//那么<=mid的地方肯定不是搜素范围
        }
        else if(nums[mid]>target)
        {
            right=mid;//这时候mid有可能是题解，不能-1
        }
        else
        {
            return mid;
        }
    }
    return nums[left]<target?left+1:left;//判断target会不会比最大的元素还大
}

第三题：寻找旋转排序数组中的最小值

然后是：寻找旋转排序数组中的最小值

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：
若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]
注意，数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

说直白一点就是，在这种形状中的数组中寻找最小值。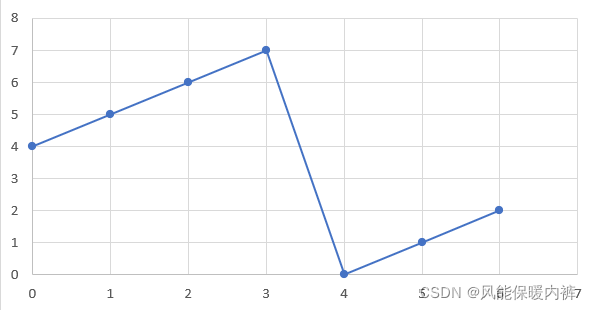

解题思路

其实这个题可以直接一次遍历找出最小值，但是这样就没什么意思了。我分享一下二分法

题目给定函数： int findMin(int* nums, int numsSize)

1. 还是一样啊，先定义int left = 0 ,right =numsSize - 1 ；还有循环体while(left < right) ，我们依旧是要拿mid跟left和right作对比，根据对比情况得到最小值的位置。
2. 如果nums[mid] > nums[left]（如下图），这就说明最小值的下标肯定是在mid右边的，不能是mid和mid左边的下标，我们就要更新一下左边界：left = mid + 1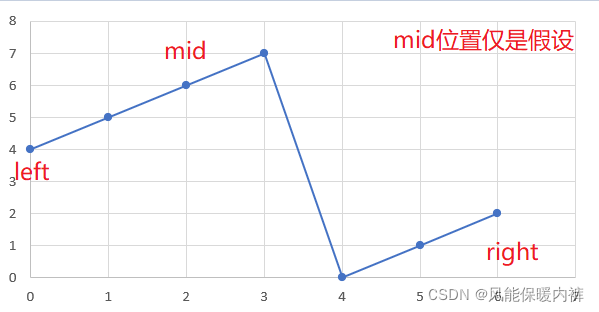
3. 如果nums[mid] < nums[right]（如下图），我要就要更新一下右边界，但是这里要不要 -1呢，我们分析一下：因为nums[mid] < nums[right]，然而nums[mid]本身有可能是最小值的，所以mid有可能就是最小值的下标，所以这个地方不能把mid下标移出搜索区域，即right = mid。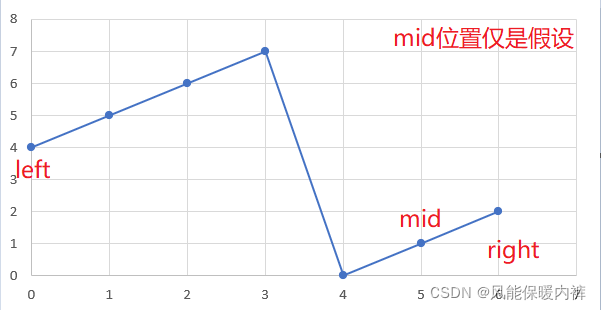
4. 说完大于和小于的情况，那会不会出现nums[mid] == nums[left] 或者 nums[mid]==nums[right]的情况呢？
5. ①首先我们先看一下nums[mid] == nums[right]：关于表达式int mid = left + (right - left) / 2;是有向下取整的效果的；（相反int mid = left + (right - left + 1) / 2;是有向上取整的效果的，不过先不讨论这个），所以不管怎么样，mid不会等于right。
6. ②然后是nums[mid] == nums[left] ，如果出现这种表达式，那么这个二分查找的搜索区间最长就是2（就是只剩两个元素），这样的话就只剩下面两幅图的趋势。如果是左图，那就更新right = mid，如果是右图，那就是left = mid + 1。

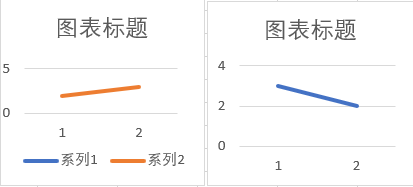
总结一下：如下

代码

int findMin(int* nums, int numsSize)    
{//不断减少查找范围
    int left=0,right=numsSize-1;
    while(left<right)  
    {
        int mid=left+(right-left)/2;
        if(nums[mid]<nums[right])
        {
            right=mid;         
        }
        else
        {
            left=mid+1;
        }
    }
    return nums[left];
}

第四题：寻找峰值

接下来：寻找峰值（学习了力扣大佬的做法）

峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。

没想到吧，这种情况下还是可以用二分法。

解题思路

题意所给函数：int findPeakElement(int* nums, int numsSize)

1. 还是一样啊，啪的一下把我的模板写出来，很快啊，先定义int left = 0 ,right =numsSize - 1 ；还有循环体while(left < right)
2. 这次不那么一样。这个题目我们只要找出峰值就行，也就是找出nums[i-1] < nums[i] < nums[i+1]。
3. 所以我们还是要找出nums[mid]，让它和右边一个元素比较即if(nums[mid] > nums[mid+1])，如果nums[mid] < nums[mid+1]，说明还在上升，但是nums[mid]肯定不是峰值，而nums[mid+1]有可能是，所以我们更新左边界left = mid + 1

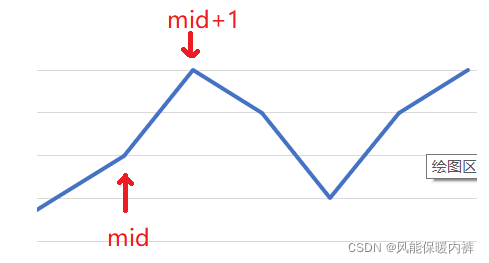
5. 相反，nums[mid] > nums[mid+1],说明nums[mid+1]肯定不是峰值，但是nums[mid]有可能是，既然有可能是，我们就不能把mid移出搜索范围，即更新右边界right = mid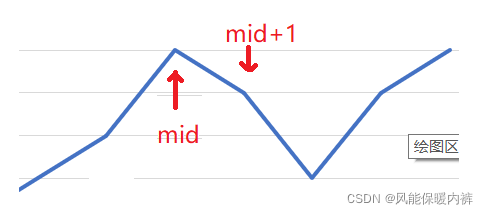
6. 然后3,4步骤循环，当left = right的时候二分结束，left即为峰值下标

代码

int findPeakElement(int* nums, int numsSize)
{
    int left=0,right=numsSize-1;
    while(left<right)
    {
        int mid=left+(right-left)/2;  //有向下取整的效果
        if(nums[mid]<nums[mid+1])   //如果是上坡（第七行）
        {  //当二分查找的区间长度时1时，这个过程也就结束了。
            left=mid+1;
        }
        else
        {
            right=mid;
        }
    }
    return left;
}

• 补充：上面代码第七行不用判断下标越界的原因是，二分查找的区间长度至少为2，而int mid = left + (right - left) / 2;是有向下取整的效果的，所以mid+1一直都在二分查找搜索的范围内

第五题：在排序数组中查找数字Ⅰ

再来一题：在排序数组中查找数字Ⅰ

统计一个数字在排序数组中出现的次数。

当然这个题有别的做法，不过我们还是来尝试一下二分查找法。

解题步骤

所给函数：int search(int* nums, int numsSize, int target)

1. 如果这个题用二分查找的方法来写：那么我们只需要找出target出现的第一个下标，再找出target出现的最后一个下标。然后后者下标 - 前者下标 + 1 = 出现次数，如图

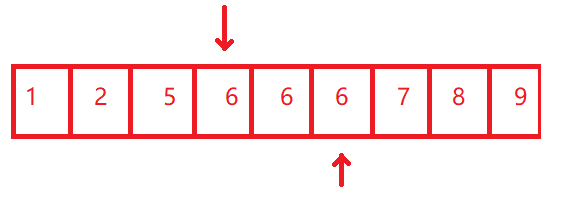
2. 然后还是一样先定义int left = 0 ,right =numsSize - 1 ；还有循环体while(left < right)

3. 所以首先我们就要找出第一个出现target位置的下标：
   ①如果nums[mid] < target，那么nums[mid]自然nums[mid] != target，而mid左边的下标也不可能是target的下标，所以我们更新一下左边界left = mid + 1

   ②如果nums[mid] = target，▲那么nums[mid]有可能是第一次出现target的下标，nums[mid-1]也有可能是第一次出现target的位置，而nums[mid+1]就不可能是第一次出现target的位置了，所以我们就可以更新右边界right = mid（不能-1，因为▲）

   ③如果nums[mid] > target，那么mid和mid右边的下标就不可能是target最后出现的位置，所以：right = mid - 1

//找出第一个出现target的下标
int SearchLeft(int* nums,int numsSize,int target)
{
    int left=0;
    int right=numsSize-1;
    while(left<right) //这个地方需要的是小于号，而不是小于等于号
    {
        int mid=left+(right-left)/2;
        if(nums[mid]<target)
        {
            left=mid+1;
        }
        else if(nums[mid]==target)
        {
            right=mid;
        }
        else
        {
            right=mid-1;
        }
    }
    //如果最终还没找到等于target的下标，那就返回0
    return nums[left]==target? left : 0;
}

4. 然后就要找出最后一次出现target的位置：
   ①诶那到这里就有点不一样了，我们这时候就要定义int mid = left + (right - left + 1) / 2这个如上文所说，这个表达式具有向上取整的效果，通俗一点说，就是int mid = left + (right - left) / 2会尽量靠近left，int mid = left + (right - left + 1) / 2会尽量靠近right

   ②所以，如果nums[mid] < target，那么mid和mid左边的值肯定不会是target处的下标，所以更新左边界left = mid + 1

   ③如果nums[mid] = target，▲mid处有可能是最后一个出现target的，但是mid左边肯定不会是最后一个出现target的，而mid右边也有可能是最后一个出现target的，因此我们缩小左边界left = mid（不能-1，就是因为▲）

   ④如果nums[mid] > target，那么mid和mid右边就不可能是最后一个出现target的，更新右边界right = mid - 1

   ⑤由于int mid = left + (right - left + 1) / 2，所以mid会尽量靠近right，所以我们二分查找结束的时候，要返回nums[right] ，而不是nums[left]。原因：我们举个例子，数组nums[2] = { 1 , 2 } target = 3的时候，这时候mid = 1，而nums[mid] < target，这时候我们更新left = mid + 1的时候，left就会越界

int SearchRight(int* nums,int numsSize,int target)
{
    int left=0;
    int right=numsSize-1;
    while(left<right)
    {
        int mid=left+(right-left+1)/2;
        if(nums[mid]<target)
        {
            left=mid+1;
        }
        else if(nums[mid]==target)
        {
            left=mid;
        }
        else
        {
            right=mid-1;
        }
    }
    //注意这边是nums[right]
    return nums[right]==target? right : -1 ;
}

代码

int SearchLeft(int* nums,int numsSize,int target)
{
    int left=0;
    int right=numsSize-1;
    while(left<right) 
    {
        int mid=left+(right-left)/2;
        if(nums[mid]<target)
        {
            left=mid+1;
        }
        else
        {
            right=mid;
        }
    }
    return nums[left]==target? left : 0;
}

int SearchRight(int* nums,int numsSize,int target)
{
    int left=0;
    int right=numsSize-1;
    while(left<right)
    {
        int mid=left+(right-left+1)/2;
        if(nums[mid]>target)
        {
            right=mid-1;
        }
        else
        {
            left=mid;
        }
    }
    return nums[left]==target? left : -1 ;
}

int search(int* nums, int numsSize, int target)
{
    if(numsSize==0)
    {
        return 0;
    }
    //如果找不到第一个出现target的下标，那就肯定找不到最后一个出现target的下标
    //所以一个返回0，一个返回-1，下面这行代码就会返回0
    return SearchRight(nums,numsSize,target) - SearchLeft(nums,numsSize,target) + 1;
}