栈以及栈实现简易计算器（实现中缀转后缀表达式以及后缀表达式的运算）

栈的概念

栈（stack）又名堆栈，它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶，相对地，把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。

栈这种数据结构可以想象成弹夹，元素先进后出，后进先出，栈为空时top指向-1，进栈top++，出栈top–

用栈实现一个正整数加减乘除的计算器

步骤：
1. 遍历表达式，如果是数字则入数栈，符号就入符号栈
2. 如果要入栈的符号的优先级小于或等于符号栈顶中的符号，则从数栈中弹出两个数字，从符号栈中弹出一个符号进行运算（次栈顶元素对于栈顶元素运算），得到的结果重新入数栈
3. 将先前的符号入符号栈

符号栈：

public class CharStack {
    private int maxSize;
    private char[] stack;
    private int top = -1;

    public CharStack(int maxSize) {
        this.maxSize = maxSize;
        this.stack =new char[this.maxSize];
    }

    /**
     * 获得栈顶元素，不弹出
     * @return
     */
    public Character getTop(){
        if (isEmpty()){
            return null;
        }
        return stack[top];
    }
    /**
     * 栈满
     */
    public boolean isFull(){
        return top == maxSize-1;
    }

    /**
     * 栈空
     */
    public boolean isEmpty(){
        return top == -1;
    }

    /**
     * 入栈
     * @param i
     */
    public void push(char i){
        if (isFull()){
            System.out.println("满栈");
            return;
        }
        stack[++top] = i;
    }

    /**
     * 出栈
     */
    public Character pop(){
        if (isEmpty()){
            System.out.println("空栈");
            return null;
        }
        return stack[top--];
    }

    /**
     * 返回符号优先值
     */
    public int priority(char o){
        if (o == '*' || o == '/'){
            return 1;
        }else if (o == '+' || o == '-'){
            return 0;
        }else {
            return -1;
        }
    }

    /**
     * 判断是不是运算符
     */
    public boolean isChar(char o){
        HashSet<Character> characters = new HashSet<>();
        characters.add('+');
        characters.add('-');
        characters.add('*');
        characters.add('/');
        return characters.contains(o);
    }

}

数栈：

public class ArrayStack {
    private int maxSize;
    private int[] stack;
    private int top = -1;

    public ArrayStack(int maxSize) {
        this.maxSize = maxSize;
        this.stack =new int[this.maxSize];
    }
	....................................
	省略了入栈，出栈，栈满，栈空的重复代码
	....................................
	/**
     * 计算
     */
    public int calculate(int num1, int num2, char o){
        int result = 0;
        switch (o){
            case '+':
                result = num1+num2;
                break;
            case '-':
                result = num1-num2;
                break;
            case '*':
                result = num1*num2;
                break;
            case '/':
                result = num1/num2;
                break;
        }
        return result;
    }
    public static void main(String[] args) {
        String s = "1";
        System.out.println(Integer.parseInt(s));
    }
}

代码实现：

public class Calculate {
    public static void main(String[] args) {
		//分别定义符号栈和数字栈
        ArrayStack numStack = new ArrayStack(10);
        CharStack charStack = new CharStack(10);

        int num1 = 0;
        int num2 = 0;
        //保存读到的符号
        char temp = ' ';
        //符号栈中取出的符号
        char ch = ' ';
        String multiNum = "";
        String expression = "50*2-10";
        for (int i=0; i<expression.length(); i++){
            temp = expression.charAt(i);//取出的符号或者数字
            if(charStack.isChar(temp)){
                try {
                    ch = charStack.getTop();
                }catch (NullPointerException e){//符号栈空直接入栈
                    charStack.push(temp);
                    continue;
                }
                //符号栈顶的优先级
                int top = charStack.priority(ch);
                // 读取到符号的优先级
                int tempNum = charStack.priority(temp);
                while (tempNum <= top && top != -1){
                    charStack.pop();//将栈中的符号先弹出
                    num1 = numStack.pop();
                    num2 = numStack.pop();
                    int cal = numStack.calculate(num2, num1, ch);
                    numStack.push(cal);
                    try {
                        ch = (char) charStack.getTop();
                        top = charStack.priority(ch);
                    }catch (NullPointerException e){
                        break;//符号栈中已经没有符号，跳出循环
                    }
                }
                //符号栈空时或temp优先级高时则直接压入temp
                charStack.push(temp);
            }else  {
                //累加多位数
                multiNum += temp;
//                如果后面是符号或已经是最后一个元素则多位数入栈
                if (i == expression.length()-1 || charStack.isChar(expression.charAt(i+1))) {
                    int val = Integer.parseInt(multiNum);
                    multiNum = "";//清空
                    numStack.push(val);//转为数字压入栈时要减去48
                }
            }
        }
        //将符号栈中的符号全部弹出并运算
        do {
            ch = charStack.pop();
            num1 = numStack.pop();
            num2 = numStack.pop();
            int cal = numStack.calculate(num2, num1, ch);
            numStack.push(cal);
        }while (!charStack.isEmpty());


        System.out.println(numStack.pop());
    }
}

在遍历表达式时要考虑多位数，所以用一个字符串拼接来记录数字
在元素出栈时要考虑空栈的结果

关于栈有一个Stack类可以使用

Stack<Object> stack = new Stack<>();

以上计算器计算的表达式不能计算带有括号的表达式，因为符号栈中没有定义，代码逻辑中也没考虑。

而后缀表达式对于计算机来说是理解友好的，中缀表达式则对于人类友好，所以有一种通用算法可以将中缀表达式转换成后缀表达式（逆波兰表达式）。

操作：

1. 初始化两个栈，分别是运算符栈s1和储存运算结果的栈s2
2. 从左到右扫描中缀表达式
3. 【1】如果是数则进s2栈，如果是运算符先与s1顶部运算符比较优先级，如果s1空或者符号是‘（’则直接进s1栈。
【2】如果运算符号优先级比栈顶运算符高也直接进s1栈（遇见符号‘（’，不比较优先级，直接入s1栈），否则将s1栈顶元素弹出并压入s2。
【3】如果符号是‘）’则一次弹出s1中元素并压入s2，直到弹出左括号为止，并将这一对括号销毁
4. 2，3两步执行到最后一个表达式元素为止，将剩余的s1栈中元素弹出并压入s2栈
5. 依次弹出s2栈的元素，逆序后就是后缀表达式。

代码中用toList把方法转换成了List结构，并且s2用了List实现，因为s2没有pop操作，并且直接输出List就不用执行第五步操作了。

public class Transfer {
    /**
     * 将表达式元素分割转换为List便于操作
     * @param str
     * @return
     */
    public static List<String> toList(String str){
        int i = 0;//索引
        ArrayList<String> list = new ArrayList<>();
        char c ;
        String mulNum = "";//多位数字符串
        for (i=0; i<str.length(); i++){
            c = str.charAt(i);
            //c是符号
            if (c > 57 || c < 48)
                list.add(""+c);
            //c是数字
            else{
                mulNum += c;
                if (i==str.length()-1 || str.charAt(i+1)>57 || str.charAt(i+1)<48) {
                    list.add(mulNum);
                    mulNum = "";
                }
            }
        }
        System.out.println(list);
        return list;
    }

    /**
     * 返回符号优先值
     */
    public static int priority(String o){
        if (o.equals("*") || o.equals("/") ){
            return 1;
        }else if (o.equals("+" ) || o.equals("-") ){
            return 0;
        }else {
            return -1;
        }
    }

    /**
     * 转换成逆波兰表达式
     * @return
     */
    public static List toRPN(String str ){

        List<String> list = toList(str);
        Stack<String> s1 = new Stack<>();
        ArrayList<String> s2 = new ArrayList<>();

        for (String s : list){
            //正则表达式，如果是一个数
            if (s.matches("\\d+")){
                s2.add(s);
                //如果s1空或者此符号是"(",直接进栈
            }else if (s1.isEmpty() || s.equals("(")){
                s1.push(s);
                //如果此符号是")"
            }else if (s.equals(")")){
                while (!s1.peek().equals("(")){
                    s2.add(s1.pop());
                }
                s1.pop();//弹出"("
                //如果运算符优先级高于s1栈顶的元素或者栈顶元素是"(",直接进栈
            }else if (priority(s)>priority(s1.peek()) || s1.peek().equals("(")){
                s1.push(s);
                //运算符优先级低于或等于s1栈顶元素
            }else {
                while (!s1.isEmpty() && priority(s)<=priority(s1.peek()))
                    s2.add(s1.pop());
                s1.push(s);
            }
        }//s1中元素弹出并压入s2
        while (!s1.isEmpty()){
            s2.add(s1.pop());
        }
        System.out.println(s2);
        return s2;
    }
    public static void main(String[] args) {
        toRPN("1+((3*6))-7+3");
    }
}

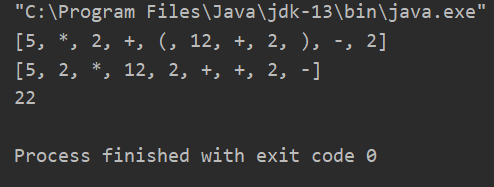
打印结果：

后缀表达式计算：
计算很简单，从左到右扫描后缀表达式，如果数字直接入栈，如果是运算符则从栈中弹出两个数字，用次栈顶元素（后弹出的那个数）对栈顶元素运算，将运算的数重新入栈，最后栈中只剩下一个数，就是结果。
（前缀表达式从右往左扫描，运算时用栈顶元素对次栈顶元素运算）

public static boolean isChar(String o){
        HashSet<String> strings = new HashSet<>();
        strings.add("+");
        strings.add("-");
        strings.add("*");
        strings.add("/");
        return strings.contains(o);
    }
    public static int operation(int num1, int num2, String o){
        int result = 0;
        switch (o){
            case "+":
                result = num1+num2;
                break;
            case "-":
                result = num1-num2;
                break;
            case "*":
                result = num1*num2;
                break;
            case "/":
                result = num1/num2;
                break;
        }
        return result;
    }
    /**
     * 计算后缀表达式
     */
    public static int calculate(List<String> list){
        Stack<String> stack = new Stack<>();
        for (String s : list){
            if (isChar(s)){
                int o1 = Integer.parseInt(stack.pop());
                int o2 = Integer.parseInt(stack.pop());
                int val = operation(o2, o1, s);
                stack.push(String.valueOf(val));
            }else {
                stack.push(s);
            }
        }
        int result = Integer.parseInt(stack.peek());
        System.out.println(result);
        return result;
    }

isChar和operation方法分别是判断是否是运算符已经对两个元素运算。

main方法：

public static void main(String[] args) {
        List list = toRPN("5*2+(12+2)-2");
        calculate(list);
    }

结果：