分析:
小Ho:这种简单的谜题就交给我吧!
小Hi:真的没问题么?
<10分钟过去>
小Ho:啊啊啊啊啊!搞不定啊!!!骨牌数量一多就乱了。
小Hi:哎,我就知道你会遇到问题。
小Ho:小Hi快来帮帮我!
小Hi:好了,好了。让我们一起来解决这个问题。
小Hi:原来是这样。。。小Ho你仔细观察这个例子:

因为相连的两个数字总是相同的,不妨我们只写一次,那么这个例子可以写成:3-2-4-3-5-1。6个数字刚好有5个间隙,每个间隙两边的数字由恰好对应了一块骨牌。
如果我们将每一个数字看作一个点,每一块骨牌看作一条边。你觉得是怎么样的呢?
小Ho:以这个例子来说的话,就是:
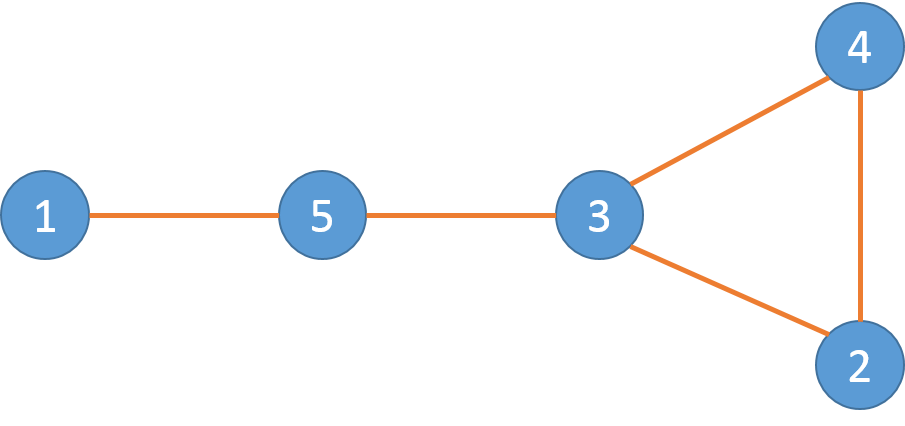
要把所有的骨牌连起来,也就是把所有的边都走一次。咦,这不是欧拉路问题么!
小Hi:没错,这问题其实就是一个欧拉路的问题,不过和上一次不一样的在于,这一次我们要找出一条欧拉路径。
小Ho:那我们应该如何来找一条路径呢?
小Hi:我们还是借用一下上次的例子吧
使用我们上一次证明欧拉路判定的方法,我们在这个例子中找到了2条路径:
L1: 4-5-2-3-6-5
L2: 2-4-1-2
假设我们栈S,记录我们每一次查找路径时的结点顺序。当我们找到L1时,栈S内的情况为:
S: 4 5 2 3 6 5 [Top]
此时我们一步一步出栈并将这些边删除。当我们到节点2时,我们发现节点2刚好是L1与L2的公共节点。并且L2满足走过其他边之后回到了节点2。如果我们在这个地方将L2先走一遍,再继续走L1不就刚好走过了所有边么。
而且在上一次的证明中我们知道,除了L1之外,其他的路径L2、L3...一定都满足起点与终点为同一个点。所以从任意一个公共节点出发一定有一条路径回到这个节点。
由此我们得到了一个算法:
在原图中找一个L1路径
从L1的终点往回回溯,依次将每个点出栈。并检查当前点是否还有其他没有经过的边。若存在则以当前点为起点,查找L2,并对L2的节点同样用栈记录重复该算法。
当L1中的点全部出栈后,算法结束。
在这里我们再来一个有3层的例子:
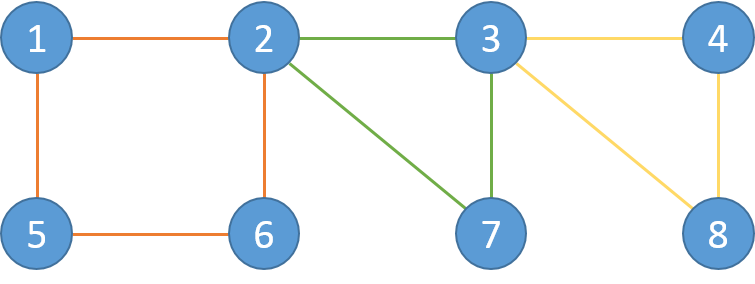
在这个例子中:
L1: 1-2-6-5-1
L2: 2-3-7-2
L3: 3-4-8-3
第一步时我们将L1压入栈S,同时我们用一个数组Path来记录我们出栈的顺序:
S: [1 2 6 5 1]
Path:
然后出栈到节点2时我们发现了2有其他路径,于是我们把2的另一条路径加入:
S: 1 [2 3 7 2]
Path: 1 5 6
此时L2已经走完,然后再开始弹出元素,直到我们发现3有其他路径,同样压入栈:
S: 1 2 [3 4 8 3]
Path: 1 5 6 2 7
之后依次弹出剩下的元素:
S:
Path: 1 5 6 2 7 3 8 4 3 2 1
此时的Path就正好是我们需要的欧拉路径。
小Ho:原来这样就能求出欧拉路,真是挺巧妙的。
小Hi:而且这个算法在实现时也有很巧妙的方法。因为DFS本身就是一个入栈出栈的过程,所以我们直接利用DFS的性质来实现栈,其伪代码如下:
DFS(u):
While (u存在未被删除的边e(u,v))
删除边e(u,v)
DFS(v)
End
PathSize ← PathSize + 1
Path[ PathSize ] ← u
#include
#include
#include
#include
#include
#include
using namespace std;
const int N = ;
int n, m, flag, top, sum, du[N], ans[], map[N][N];
void dfs(int x)
{
ans[++top] = x;
for(int i = ; i <= n; i++)
{
if(map[x][i] >= )
{
map[x][i]--;
map[i][x]--;
dfs(i);
break;
}
}
}
void fleury(int x)
{
top = ;
ans[top] = x;
while(top > )
{
int k = ;
for(int i = ; i <= n; i++)//判断是否可扩展
{
if(map[ans[top]][i] >= )//若存在一条从ans[top]出发的边 那么就是可扩展
{k = ; break;}
}
if(k == )//该点x没有其他的边可以先走了(即不可扩展), 那么就输出它
{
printf("%d ", ans[top]);
top--;
}
else if(k == )//如可扩展, 则dfs可扩展的哪条路线
{
top--;//这需要注意
dfs(ans[top+]);
}
}
}
int main()
{
while(scanf("%d%d", &n, &m) != EOF)
{
memset(du, , sizeof(du));
memset(map, , sizeof(map));
for(int i = ; i <= m; i++)
{
int x, y;
scanf("%d%d", &x, &y);
map[x][y]++; //记录边, 因为是无向图所以加两条边, 两个点之间可能有多条边
map[y][x]++;
du[x]++;
du[y]++;
}
flag = ; // flag标记开始点。 如果所有点度数全为偶数那就从1开始搜
sum = ;
for(int i = ; i <= n; i++)
{
if(du[i] % == )
{
sum++;
flag = i;// 若有奇数边, 从奇数边开始搜
}
}
if(sum == || sum == )
fleury(flag);
}
return ;
}
转:https://www.cnblogs.com/wd-one/p/4584182.html
hiho欧拉路&#183;二 --------- Fleury算法求欧拉路径
hiho欧拉路·二 分析: 小Ho:这种简单的谜题就交给我吧! 小Hi:真的没问题么? <10分钟过去> 小Ho:啊啊啊啊啊!搞不定啊!!!骨牌数量一多就乱了. 小Hi:哎,我就知道你会遇 ...
HihoCoder1181欧拉路(Fleury算法求欧拉路径)
描述 在上一回中小Hi和小Ho控制着主角收集了分散在各个木桥上的道具,这些道具其实是一块一块骨牌. 主角继续往前走,面前出现了一座石桥,石桥的尽头有一道火焰墙,似乎无法通过. 小Hi注意到在桥头有一张 ...
Fleury算法 求欧拉回路
Fleury算法 #include #include #include #include
【欧拉回路】【欧拉路径】【Fleury算法】CDOJ1634 记得小苹初见,两重心字罗衣
Fleury算法看这里 http://hihocoder.com/problemset/problem/1181 把每个点看成边,每个横纵坐标看成一个点,得到一个无向图. 如果新图中每个点的度都是偶数 ...
C++迪杰斯特拉算法求最短路径
一:算法历史 迪杰斯特拉算法是由荷兰计算机科学家狄克斯特拉于1959 年提出的,因此又叫狄克斯特拉算法.是从一个顶点到其余各顶点的最短路径算法,解决的是有向图中最短路径问题.迪杰斯特拉算法主要特点是以 ...
poj 3565 uva 1411 Ants KM算法求最小权
由于涉及到实数,一定,一定不能直接等于,一定,一定加一个误差<0.00001,坑死了…… 有两种事物,不难想到用二分图.这里涉及到一个有趣的问题,这个二分图的完美匹配的最小权值和就是答案.为啥呢 ...
HDU-1233 还是畅通工程 (prim 算法求最小生成树)
prim 算法求最小生成树 还是畅通工程 Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Oth ...
Dijkstra算法求单源最短路径
Description 在每年的校赛里,所有进入决赛的同学都会获得一件很漂亮的t-shirt.但是每当我们的工作人员把上百件的衣服从商店运回到赛场的时候,却是非常累的!所以现在他们想要寻找最短的从商店 ...
ZOJ Problem - 2588 Burning Bridges tarjan算法求割边
题意:求无向图的割边. 思路:tarjan算法求割边,访问到一个点,如果这个点的low值比它的dfn值大,它就是割边,直接ans++(之所以可以直接ans++,是因为他与割点不同,每条边只访问了一遍) ...
随机推荐
同一行多个div宽度自适应布局
主要运用到的是:布局神器display:table-cell 元素两端对齐 第一个案例是让两个元素分别向左和向右对齐,如果是过去,我一定会用float来实现,但其实用table可以这么做: 自动平均划 ...
sql语句的匹配
like 的通配符有两种 %(百分号):代表零个.一个或者多个字符. _(下划线):代表一个数字或者字符. 1. name以"李"开头 where name like '李%' 2 ...
影响 PHP 行为的扩展和网络函数
THINKPHP 默认模板路径替换
APP_PATH // 当前项目目录APP_NAME // 当前项目名称 ACTION_NAME // 当前操作名称 CACHE_PATH // 项目模版缓存目录 CONFIG_PATH //项目配置 ...
368. Largest Divisible Subset -- 找出一个数组使得数组内的数能够两两整除
Given a set of distinct positive integers, find the largest subset such that every pair (Si, Sj) of ...
消息点击事件的响应链---hitTest:withEvent:方法
*当用户点击屏幕时,会产生一个触摸事件,系统会将触摸事件加入到 UIApplication管理事件队里中 *UIApplication 会从事件队列中取出最前面的事件进行分发以便处理,通常,先发送事件 ...
CEP简介
CEP即Complex Event Processing缩写,翻译过来就是复杂事件处理(复合事件可能更加准确). 1.为什么我们需要CEP?CEP是具有实时分析以及快速响应等等功能.下面让我们通过 ...
jQuery 快速入门教程
内容目录 jQuery 入门 什么是jQuery 如何使用jQuery jQuery的运行原理 如何选择jQuery版本 ready() 准备就绪时执行代码 jQuery 核心:选取元素 使用jQue ...
java并发:Synchronized 原理
1.同步代码块: 反编译结果: monitorenter : 每个对象有一个监视器锁(monitor).当monitor被占用时就会处于锁定状态,线程执行monitorenter指令时尝试获取moni ...
thymeleaf 货币格式化 数字格式化问题
格式化数字对象 ${'¥'+#numbers.formatDecimal(pro.price,0,'COMMA',2,'POINT')} ${'¥'+#numbers.formatDecimal(pr ...