文章目录

一、树是什么？
- 树的特点
二、二叉树
- 1.概念及特点
- 2.常见的二叉树
三、二叉树的遍历（递归和迭代）
总结

一、树是什么？

树是一种非线性的数据结构，它是由n(n >= 0)个有限结点组成的一个具有层次关系的集合。(线性数据结构就是：线性表，数组，栈，链表，队列，字符串…元素之间逻辑上一个挨着一个，呈值直线排列)把它叫做树是因为它看起来像一颗倒着的树，意思就是根朝上，叶子朝下。

树的特点

有一个特殊的结点，称为根节点，根节点没有前驱结点。
除根节点外，其余节点被分成M(M > 0) 个互不相交的集合T1、T2、…、Tm,其中每一个集合又是一颗子树。每颗子树的根节点有且只有一个前驱，可以有0个或者多个后继。
树是递归定义的。
子树不相交。
除了根节点没有父节点之外，每个节点有且只有一个父节点。
树，边的个数x，和树中节点的个数n，x=n - 1（每个节点都有一个父节点，只有根节点没有父节点）
节点和树的“度” ： 节点的度是指该节点中包含的子树个数称为该节点的度。树的度：树中最大的节点的度就称为子树的度。
叶子节点： 度为0的节点。即该节点没有任何子树。
节点的层次(高度)： 从根节点开始计算，根节点为第一层，根节点的左子树和右子树是第二层，以此类推。
树的高度： 当前树中节点高度最大的即为树的高度。

二、二叉树

1.概念及特点

树中节点最大的度为2的树称之为二叉树。
在二叉树中一个节点最多有两颗子树，二叉树节点的度 <=2；子树有左右之分，左右顺序不能颠倒。

深度为k的二叉树中，最多存在 (2^k )- 1 个节点。
在第k层，该层最多有 2^(k-1) 个节点。
任意二叉树都满足节点个数n和边长x具备 :
x = n -1

2.常见的二叉树

满二叉树： 在该二叉树中，每一层节点个数都是最大值，每一层节点个数都是拉满了。
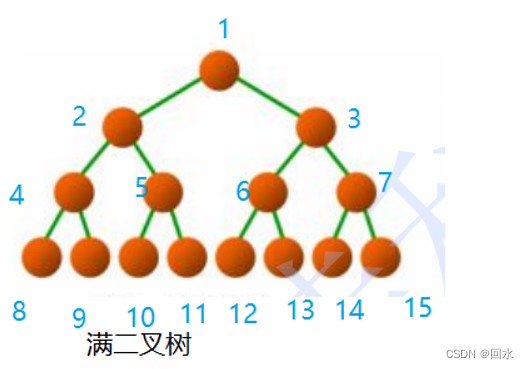
完全二叉树： 除了最深的一层节点不满，其余层都满了。满二叉树就是一种特殊的完全二叉树。完全二叉树中不存在只有右子树，没有左子树的节点。若存在度为1的节点，那么该节点必然只有左子树，且该节点有且只能有一个。完全二叉树的节点编号(根节点为1)和满二叉树完全一致。

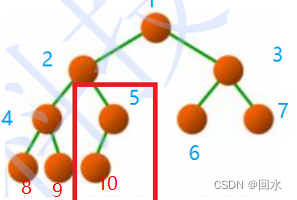
在这里插入图片描述

二分搜索树(BST)
节点的值之间有一个大小关系：
左子树的值 < 根节点的值 < 右子树的值
如图：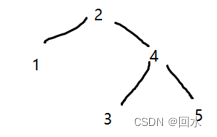

若在BST中查找一个元素，其实就是二分查找。
平衡二叉树
该树中任意一个节点的左右子树高度差 <= 1。

三、二叉树的遍历（递归和迭代）

按照一定的顺序访问这颗树的所有元素，做到不重复，不遗漏。
对于二叉树来说，一共有四种遍历方式

前序遍历(根左右) 节点第一次访问的时候就输出。
中序遍历(左根右) 节点第二次访问的时候输出。
后序遍历(左右根) 节点第三次访问的时候输出。
层序遍历(从根节点开始，一层一层去遍历)
前三种遍历方式属于深度优先遍历，层序遍历属于广度优先遍历。

我们自己定义一个二叉树：

比如我们要手写出这颗二叉树的中序遍历，按照上面所说的第二次访问节点输出，有以下流程：

先一路走到 D ,一路上过来的节点都属第一次访问，不输出，然后访问 D 的左子树，发现为空，倒回来再走到 D ，此时D就是第二次访问，进行输出，然后再访问D的右子树，发现为空，再倒回到D。
D这个节访问完毕后，倒回到B节点，此时B是第二次访问，输出B,然后访问B的右子树。
E节点是第一次访问，左根右，继续往左走，走到G，继续访问G的左子树，发现为空，倒回去访问G，此时G是第二次访问，进行输出；再去访问G的右子树，节点H是第一次访问，继续往左走，H的左子树为空，倒回去走H此时H是第二次访问，进行输出。
4.此时我们已经输出了 D B G H,剩下的节点以次类推就行。
那么上面这颗二叉树的遍历代码应该如何去写呢？我们首相应该想到的是递归，因为二叉树就是一个天然的递归结构。

3.1自定义二叉树

public void build() {
		//先将所有的节点值保存到node中
        TreeNode<Character> node = new TreeNode<>('A');
        TreeNode<Character> node1 = new TreeNode<>('B');
        TreeNode<Character> node2 = new TreeNode<>('C');
        TreeNode<Character> node3 = new TreeNode<>('D');
        TreeNode<Character> node4 = new TreeNode<>('E');
        TreeNode<Character> node5 = new TreeNode<>('F');
        TreeNode<Character> node6 = new TreeNode<>('G');
        TreeNode<Character> node7 = new TreeNode<>('H');
        //根据上图连接二叉树
        //A节点的左子树是B,也就是node1，下面的节点以此类推
        node.left = node1;
        node.right = node2;
        node1.left = node3;
        node1.right = node4;
        node2.right = node5;
        node4.left = node6;
        node6.right = node7;
        //根节点是A
        root = node;
        //自定义类型TreeNode类保存树的左右子树和节点值
        private class TreeNode<E> {
        	//当前结点的值
        	E val;
        	//左子树的根
        	TreeNode<E> left;
        	//右子树的根
        	TreeNode<E> right;

        	public TreeNode(E val) {
        
        		this.val = val;
        
        	}
	}
}

3.2 前序遍历(递归)

代码如下：

	//这里不太明的话可以按照我的代码自己画一下递归展开图，就会容易理解很多
	public void preOrder(TreeNode root) {
		//判断传进来的节点是否为空
        if (root == null) {
            return;
        }
        //前序遍历是根左右
        // 1.先打印根节点的值
        System.out.print(root.val + " ");
        //2.递归去访问左子树
        preOrder(root.left);
        //3.递归访问右子树
        preOrder(root.right);
    }

定义测试类：

public class TreeTest {
	public static void main(String[] args) {
        MyBinTree binTree = new MyBinTree();
        binTree.build();
        System.out.println("前序遍历：");
        binTree.preOrder(binTree.root);
    }
}

运行结果如下：
在这里插入图片描述

3.3 前序遍历(迭代)

public List<Character> preorderNoRecursion(TreeNode root) {
        List<Character> ret = new ArrayList<>();
        if (root == null) {
            return ret;
        }
        Deque<TreeNode> stack = new LinkedList<>();
        stack.push(root);
        while(!stack.isEmpty()) {
            TreeNode node = stack.pop();
            //添加根结点
            ret.add((Character) node.val);
            //因为栈是先进后出的，所以先添加右子树，后添加左子树
            //下一次循环开始的时候，先添加到数组ret中的就是左子树的值了
            if (node.right != null) {
                stack.push(node.right);
            }
            if (node.left != null) {
                stack.push(node.left);
            }
        }
        return ret;
    }

定义测试类：

public class TreeTest {
	public static void main(String[] args) {
        MyBinTree binTree = new MyBinTree();
        binTree.build();
        System.out.println("前序遍历：");
        System.out.println(binTree.preorderNoRecursion(binTree.root));
    }
}

运行结果如下:
在这里插入图片描述

3.4.中序遍历(递归)

代码如下：

public void inOrder(TreeNode root) {
        if (root == null) {
            return;
        }
        //先访问左子树
        inOrder(root.left);
        //打印当前根节点的值
        System.out.print(root.val + " ");
        //再访问右子树
        inOrder(root.right);
    }

大家自己在测试类里面调用中序遍历，我这里就不再重复写了

运行结果如下：
在这里插入图片描述

3.5 中序遍历(迭代)

public List<Object> inorderTraversal(TreeNode root) {
        List<Object> ret = new ArrayList<>();
        if (root == null) {
            return ret;
        }
        Deque<TreeNode> stack = new LinkedList<>();
        TreeNode node = root;
        //依旧用栈保存，栈不为空，或者节点不为空都进行迭代
        while (node != null || !stack.isEmpty()) {
        //节点不为空时，把左子树的所有结点都入栈，因为栈是后进先出的
        //所以最后一个入栈的一定是当前二叉树左子树的最后一个结点
            while (node != null) {
            //先一路向左走到底
                stack.push(node);
                node = node.left;
            }
            //此时node为空，弹出栈顶元素，就是第一个左子树为空的节点
            //左根右，先将最后一个节点弹出，将其添加到数组中
            node = stack.pop();
            ret.add(node.val);
            //再去看看当前结点有无右子树
            node = node.right;
        }
        return ret;
    }

运行结果如下:
在这里插入图片描述

3.6 后序遍历(递归)

public void postOrder(TreeNode root) {
        if (root == null) {
            return;
        }
        //左子树
        postOrder(root.left);
		//右子树
        postOrder(root.right);
		//打印根节点的值
        System.out.print(root.val + " ");
    }

3.7 后序遍历(迭代)

后序遍历的迭代写法还是有点难度的，左右根，根节点第三次访问的时候才能出栈。

先一路向左走到底，此时栈中栈顶就是第一个左子树为空的节点。
难点就在于如何得知这个节点是第三次访问到：就是左右子树都遍历了！
如果node == null，说明左子树已经走完了，那右子树如何去确定呢？引用一个新的变量prev，prev代表上一个完全访问结束的节点。
如果node.right != null && prev != node.right;这就代表node的右子树还不为空，且没完全访问。
每当一个节点完全访问(出栈)，就让prev指向最新的完全访问的节点。当node.right == null || node.right == prev,右子树就可以输出。

public List<Object> postorderNoRecursion(TreeNode root) {
        List<Object> ret = new ArrayList<>();
        if (root == null) {
            return ret;
        }
        Deque<TreeNode> stack = new LinkedList<>();
        TreeNode node = root;
        //prev代表上一个完全处理完毕的节点
        TreeNode prev = null;
        while (node != null || !stack.isEmpty()) {
        //先一路向左走到底
            while (node != null) {
                stack.push(node);
                node = node .left;
            }
            //查看当前栈顶元素情况
            node = stack.pop();
            //检查右子树情况
            if (node.right == null || prev == node.right) {
            //此时右子树为空或者右子树已经被处理完毕
            //此时可以输出node节点
                ret.add(node.val);
                //node节点就是最新处理完毕的节点
                prev = node;
                //将node置空，继续从栈顶取出元素
                //如果不置空，下一次循环开始的时候，当前节点又会被入栈，就死循环了
                node =null;
            } else {
                //此时node.right!=null且没被访问过，把当前节点再入栈，继续访问右子树
                stack.push(node);
                node= node.right;
            }
        }
        return ret;
    }

运行结果如下：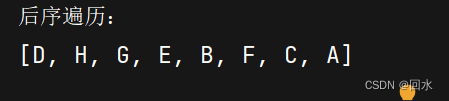
在这里插入图片描述

总结

这就是关于二叉树的四种遍历方式，很多二叉树的问题其实都是二叉树遍历问题的延伸。后面会继续给大家讲解。谢谢

原文链接：https://blog.csdn.net/weixin_50262394/article/details/124967083