1介绍

图数据结构在很多位置都有引用，例如网络爬虫，地图应用(最近距离，最短时长推荐)，社交网络分析(社交关系，好友推荐),舆情控制等领域。

2 图的基本概念

2.1 定义性质

图是由顶点集合(vex_set)，边集合(arc_set)。
度：一个顶点与之相邻的边；对于有向图则分为出度和入度

2.2 分类

按照方向区分：有向图和无向图
按权重来区分：有向权重图，无向权重图。
按照功能来区分：连通图和非连通图

3 图的存储方式

图的存储主要是顶点和边。
常见的图的存储方式：链接矩阵和链接表

3.1 链接矩阵

顶点集合：用一维数组方式存储
边集合：用二维数组方式存储

出度：行 1的个数和
入度：列 1的个数和。
优点：很容易算出连接关系，以及结点的度。
缺点：存储空间复杂度大，空间利用率不高。对于无向图只需要存储一半。

3.2 链接表

实际工程中应用链接表。
顶点集合：一维数组存储
边集合：链接表

有向图

缺点：无法计算入度

无向图

优点：度比较好计算

逆链接表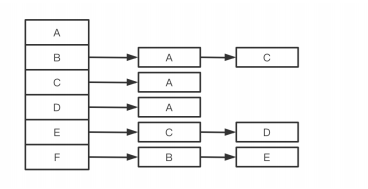

4 图的遍历

图的遍历方式主要两种：深度优先和广度优先，俗称dfs，bfs。
从图中某一个顶点触发，访问图中其余顶点，每个顶点被访问一次且只被访问一次。
可以从图中任意一点进行发起遍历。

1 缺点一条搜索路径
2 确保每个顶点都访问到
3 每个顶点只能被访问一次

设置辅助数组visited，数组元素的初始均为false，一旦遍历过后就设置为true.

4.1 dfs

深度优先：分有向图和无向图两类：
主要思想：利用递归，栈方式实现。加上本来就有辅助数组visited。

    // 对图进行深度优先遍历 (不能遍历删除)
    void DFSTraverse(vector<bool> &visited, VisitFunc func) {
        for (size_t i = 0; i < _graph_vex.size(); i++) { // 有多个
            if (!visited[i]) {
                _dfs_traverse(i, visited, func);
            }
        }
    }

// 回溯 函数堆栈来实现 实际开发过程 图纵深  尾递归
// 所有的递归 都能够转化为 递推
    void _dfs_traverse(int idx, vector<bool> &visited, VisitFunc func) {
        if (visited[idx]) return;
        visited[idx] = true;
        func(_graph_vex[idx]);
        auto &arclist = _graph_arc[idx];
        for (auto iter = arclist.begin(); iter != arclist.end(); iter++) {
            int next = INDEX(*iter);
            if (!visited[next]) {
                _dfs_traverse(next, visited, func);
            }
        }
    }

应用：
检测连通分量的个数；
两个点是否在⼀个连通分量中；
检测是否构成环；从⼀个点出发能否回到出发点；

4.2 bfs

广度优先：分有向图和无向图两类：
主要用队列来加上visited数组来实现。

    // 对图进行广度优先遍历 (不能遍历删除)
    void BFSTraverse(vector<bool> &visited, VisitFunc func) {
        for (size_t i = 0; i < _graph_vex.size(); i++) { // 可能出现多个连通图
            if (!visited[i]) {
                _bfs_traverse(i, visited, func);
            }
        }
    }

    void _bfs_traverse(int idx, vector<bool> &visited, VisitFunc func) {
        deque<int> queue;
        queue.push_back(idx);
        visited[idx] = true;
        func(_graph_vex[idx]);
        while (0 != queue.size()) {
            int i = queue.front(); queue.pop_front();
            auto &arclist = _graph_arc[idx];
            for (auto iter = arclist.begin(); iter != arclist.end(); iter++) {
                int next = INDEX(*iter);
                if (!visited[next]) {
                    queue.push_back(next);
                    visited[next] = true;
                    func(_graph_vex[next]);
                }
            }
        }
    }

应用：
游戏中找寻路径问题；不过一般也不用这个，而是采用A*算法实现

5 dijkstra算法

该算法主要解决最短路径问题，采用贪心思想。
对象是：权重图
核心过程：每次从路径最短的点出发遍历相邻边，检测修改路径值（确保相邻点也最短），从未被确认路径最短的订单集合中选择最短路径的点，将该点加入确认路径最短的订单集合，并将该点作为下次遍历相邻边的出发点。
核心流程：更新，扫描，修改

void CGraph::Dijkstra(VexType s, vector<bool> &visited, vector<int> &dis, vector<int> &parend)
{
    int iStart = _get_idx(s);
    if (-1 == iStart) {count << "start not exists!" << endl;return;}

    visited[iStart] = true;
    dis[iStart] = 0;
    parent[iStart] = iStart

    int i = iStart;
    while(true){
        //更新 相连节点的距离信息
        auto &arclist = _graph_arc[i];
        int min = INF, midx = -1;
        for(auto iter = arclist.begin(); iter != arclist.end(); iter++){
            int idx = INDEX(*iter);
            int wgt = WEIGHT(*iter);
            if (dis[idx] > wgt + dis[i]){
                dis[idx] = wgt + dis[i];
                parent[idx] = i;
            }
        }

        //扫描
        for(size_t j = 0; j < dis.size(); j++){
            if (!visited[j] && min > dis[j]){
                min = dis[j];
                midx = j;
            }
        }

        if (midx == -1) break;

        //重新选取点
        visited[midx] = true;
        i = midx;
    }

}

6 动态规划hp

这块主要是寻找状态转移方程，如果找到了就解决了。

7 简单封装一个图类

代码：https://github.com/hengfengyaoren/Data-Structure-Algorithm/tree/main/graph

参考博客：
https://mp.weixin.qq.com/s/UCTjKA7olFb00C6CLlqHAA