切映射

这一段我并看不懂，基本上照搬北京大学出版社谭小江、伍胜健《复变函数简明教程》

• 切空间 设$p=(0,0)$是$\mathbb R^2$的原点，$l:t\mapsto(x(t),y(t))$是过$p$点的一条光滑曲线，$p=(x(0),y(0))$，则$\alpha=(x'(0),y'(0))$是曲线$l$在$p$点的切向量。将所有经过$p$点的光滑曲线在$p$点的切向量的全体记为$T_p$，则$T_P$是一个线性空间，称为$\mathbb R^2$在$p$点的切空间。
• 如果$f(x,y)=(u(x,y),v(x,y))$是$p$点邻域内到$q=(0,0)$点邻域内的一个可微映射，且$f(0,0)=(0,0)$，则对过$p$点的光滑曲线$l:t\mapsto(x(t),y(t))$，$f(l):t\mapsto f((x(t),y(t))$是经过$q$点的一条光滑曲线。$\beta=\left(\dfrac{\mathrm du}{\mathrm dt}(0),\dfrac{\mathrm dv}{\mathrm dt}(0)\right)$是$f(l)$在$q$点的切向量。$f:l\mapsto f(l)$诱导了$f^*:\alpha\mapsto \beta$,从而有$f^*:T_p\to T_q$，这个映射称为切映射。

$f^*$是$f$的线性项，$f^*$对应的矩阵就是$f$在$p=(0,0)$处的Jacobi矩阵

$$\beta = f^* \alpha$$

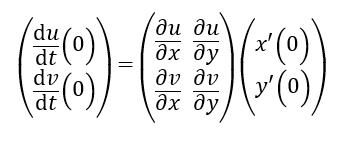
如果利用复变量$z$来表示映射，那么$l$可以表示为$z(t)=x(t)+iy(t)$，切向量$\alpha=z'(0）=x'(0)+iy'(0))$.令$f(z)=u+iv$，则切映射可以表示为

$$f^*:\alpha\mapsto \beta=\left.\dfrac{\mathrm df(z(t))}{\mathrm dt}\right\vert_{t=0}=\dfrac{\partial f}{\partial z}z'(0)+\dfrac{\partial f}{\partial \bar z}\bar z'(0)$$
这个映射是实线性的，但是不一定是复线性的。当 $\dfrac{\partial f}{\partial \bar z}\ne 0$时，由于 $\bar z'(0)$，映射不再是复线性的了，即
$$f^*(c_1\alpha_1+c_2\alpha_2)=c_1f^*(\alpha_1)+c_2f^*(\alpha_2)$$ 仅在 $c_1,c_2$为实数的时候成立。

全纯切映射

如果$f$是解析的，那么切映射是复线性的，这时定义

$$T'_{z_0}=\left\{\dfrac{\mathrm d z(0)}{\mathrm dt}\middle |z(t)是经过z_0的可微曲线，z(0)=z_0\right\}$$
称为$z_0$点的全纯切面.

对于解析函数$f$，称

$$f^*:T'_{z_0}\to T'_{f(z_0)}$$
为全纯切映射.

保角映射