题目

[BalkanOI 2011] timeismoney | 最小乘积生成树

分析

将各种生成树对应边的 $a$ 值之和作为 $x$ 坐标，$b$ 值之和作为 $y$ 坐标，那么我们需要求一个 $x\times y$ 最小的点。

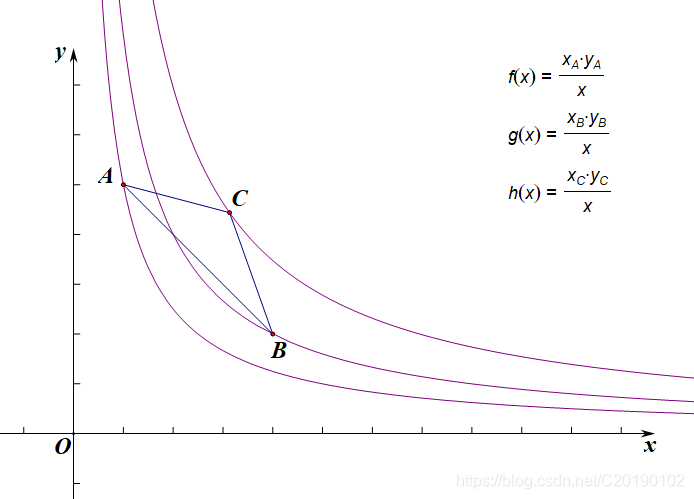
如图，如果某点 $C$ 在直线 $AB$ 上方，$x_c\times y_c$ 必然不是最小的（因为它对应的反比例函数图像在 $A$ 或 $B$ 的上方），因此 $C$ 不可能是最优的，我们找下凸包即可。

由于我们不知道具体有哪些点，不能用传统的某些方法，于是大佬发现了基于分治的 Quick Hull 快速凸包算法，算法流程如下：

1. 找到横坐标最小的点 $A$、纵坐标最小的点 $B$。
2. 直线 $AB$ 将平面分成两个部分，由于我们是找下凸包，所以在直线 $AB$ 的下方找到与直线 $AB$ 距离最远的点 $C$。
3. 对于直线 $AC$，递归第 2 步。
4. 对于直线 $CB$，递归回到第 2 步。
5. 当找不到这样的点 $C$ 时结束递归。

问题变为如何求直线 $AB$ 与其距离最大的点 $C$。$C$ 与 $AB$ 的距离看作 $△ABC$ 的高，由于底 $AB$ 是定值，只需要找使 $S_{△ABC}$ 最大的 $C$ 点。又有 $S_{△ABC}=\frac{|\overrightarrow{AC}\times \overrightarrow{AB}|}{2}$，带入坐标形式可得 $$\begin{array}{rl}2S_{△ABC}=& (x_C-x_A)(y_B-y_A)-(y_C-y_A)(x_B-x_A)\\ =& (y_B-y_A)x_C-(x_B-x_A)y_C+P\end{array}$$ $P$ 是常数，于是我们只用求 $(y_B-y_A)x_C-(x_B-x_A)y_C$ 的最大值，又 $x_C={\sum }_{e\in T}{a}_e,y_C={\sum }_{e\in T}{b}_e$ 可以用分配率拆开，于是将每条边的边权设为 $(y_B-y_A)a_e-(x_B-x_A)b_e$，跑一边最大生成树即可。

判断边界只需判断找到的点 $C$ 是否在直线 $AB$ 下方，同过叉积 $x_1{y}_2-x_2{y}_1$ 得到有向面积，若为负数说明向量 $2$ 在向量 $1$ 的顺时针方向，因此计算 $\overrightarrow{AC}$ 与 $\overrightarrow{AB}$ 的叉积是否非正即可。

代码

#include <bits/stdc++.h>

int Read() {
	int x = 0; char c = getchar();
	while (c < '0' || c > '9')
		c = getchar();
	while (c >= '0' && c <= '9')
		x = x * 10 + (c ^ 48), c = getchar();
	return x;
}

const int MAXN = 200;
const int MAXM = 10000;
const int INF = 0x7fffffff;

int N, M;
struct Edge {
	int u, v, a, b, w;
} E[MAXM + 5];

struct Vector {
	int x, y;

	Vector operator - (const Vector &other) const {
		return { x - other.x, y - other.y };
	}
	int operator * (const Vector &other) const {
		return x * other.y - y * other.x;
	}
} Ans = { INF, INF };

int Par[MAXN + 5];

int Find(const int &u) {
	return Par[u] == u ? u : (Par[u] = Find(Par[u]));
}

Vector Kruscal() {
	for (int i = 1; i <= N; i++)
		Par[i] = i;
	std::sort(E + 1, E + M + 1, [](const Edge &i, const Edge &j) {
		return i.w < j.w;
	});
	Vector ret = { 0, 0 };
	int cnt = 0;
	for (int i = 1; i <= M && cnt < N - 1; i++) {
		int u = E[i].u, v = E[i].v;
		if (Find(u) != Find(v)) {
			Par[Find(u)] = Find(v);
			ret.x += E[i].a, ret.y += E[i].b;
			cnt++;
		}
	}
	return ret;
}

void Update(const Vector &cur) {
	long long x = (long long)cur.x * cur.y, y = (long long)Ans.x * Ans.y;
	if ((x < y) || (x == y && cur.x < Ans.x))
		Ans = cur;
}

void Solve(const Vector &A, const Vector &B) {
	for (int i = 1; i <= M; i++)
		E[i].w = -(E[i].a * (B.y - A.y) - E[i].b * (B.x - A.x)); // 方便求最小生成树
	Vector C = Kruscal();
	Update(C);
	if ((C - A) * (B - A) <= 0)
		return;
	Solve(A, C), Solve(C, B);
}

int main() {
	N = Read(), M = Read();
	for (int i = 1; i <= M; i++)
		E[i].u = Read() + 1, E[i].v = Read() + 1, E[i].a = Read(), E[i].b = Read();
	for (int i = 1; i <= M; i++)
		E[i].w = E[i].a;
	Vector A = Kruscal(); Update(A);
	for (int i = 1; i <= M; i++)
		E[i].w = E[i].b;
	Vector B = Kruscal(); Update(B);
	Solve(A, B);
	printf("%d %d", Ans.x, Ans.y);
	return 0;
}