目录
0 引言
临时想到一个问题Mark一下供参考,
对于有遮挡的行人或者物体识别,或者泛化为不全的模式识别问题。
是否可以从矩阵计算的角度,引入某个矩阵分解方式去把整个图片分成:
没被遮挡的公共的在多个图片中一致的landmark 因子和体现在不同图片中的无规律的遮挡因子。
凭我的经验感觉可以去了解一下subspace,稀疏表示以及矩阵分解等知识,也许可以做一些思考和尝试。
有想法了可以找我讨论。
前三节是学习和复习记录,第四节的其他发现感觉有用,最后的思考和总结放在结束语部分。
1 模式识别
首先,看看百科上的定义
模式识别(Pattern recognition),就是通过计算机用数学技术方法来研究模式的自动处理和判读。
或者用更直白的一个定义
所谓模式识别的问题就是用计算的方法根据样本的特征将样本划分到一定的类别中去。
用人话讲,就是人制定出一些规则输入给电脑,电脑应用规则去处理和操作信息,从而能够描述、辨认、分类或者解释某些信息。
而模式识别中的模式就可以理解为一种抽象信息,例如语音识别里的声音的波形图等。而如果需要识别的东西一开始没有什么确定的信息,那就要通过数学建模等方式抽象出一些信息以使机器有能力执行和完成识别任务。
2 有遮挡的行人或物体识别
其实主要的课题是行人重识别,就是在图像或监控视频中重新找到我想找到的一个人。这个任务其实不算难,也是通过深度学习来提取特征再分类特征信息从而找人。
而老师语义中的麻烦之处就是“有遮挡”三个字。对于原本的这个问题,师兄和老师的解决之道大概是把人分成几个主要部分,比如说头、身子、手臂、双腿和脚,然后每一部分单独提取特征并与其他图像的这一部分去进行比对。所以在遇到遮挡问题的时候,就可以不比较遮挡部分的信息,只分析和比较其他部分的信息,以达到不被遮挡部分的像素影响总体找人精确度的目的。
3 矩阵计算及分解
3.1 子空间(Subspace)
子空间指的是维度小于全空间的部分空间。
举个例子来说明的就是,我所在的房间内部是一个空间,或者我把它定义成最大的空间(全空间);那么,桌面所在的这个面上的空间,就是一个子空间。
子空间也需要满足封闭性,也就是桌面上的一个向量加另一个向量得到的还在这个桌面之上。
3.2 稀疏表示(Sparse Representations)
稀疏表示是用较少的基本信号的线性组合来表达大部分或者全部的原始信号。
很好理解。用个不恰当的比喻来说明就是,一套《冰与火之歌》有超级多的字儿,但其是由26个英文字母和空格标点什么的组成的。在图像领域的话就是,一个图片数据集(包含各种动物)作为一个字典,那么用尽量少的图片去表示人类,这个过程就可以理解为是一个稀疏表示。
在数学上表示[1]就是,arg min ∥ Y i − D × X i ∥ 2 2 s.t. ∥ X i ∥ 0 < T \arg \min \left\|Y_{i}-D \times X_{i}\right\|_{2}^{2} \quad \text { s.t. }\left\|X_{i}\right\|_{0}<Targmin∥Yi−D×Xi∥22 s.t. ∥Xi∥0<T
其中,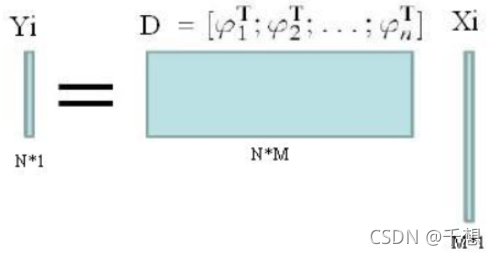
具体说明请参看参考[1]。
3.2 矩阵分解(Matrix Decomposition)
具体说明请参看参考[2]。
3.2.1 LU分解
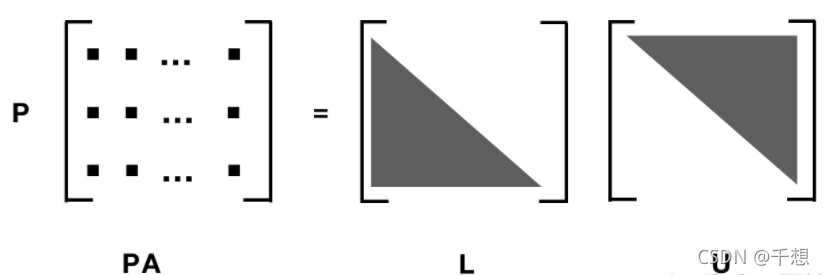
3.2.2 QR分解
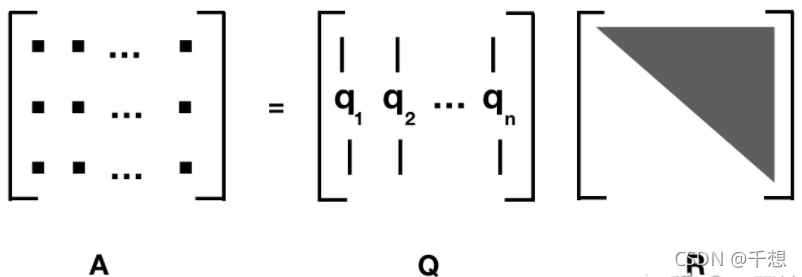
其中,Q是正交矩阵;QR分解可以用Gram–Schmidt法去完成。
3.2.3 特征分解
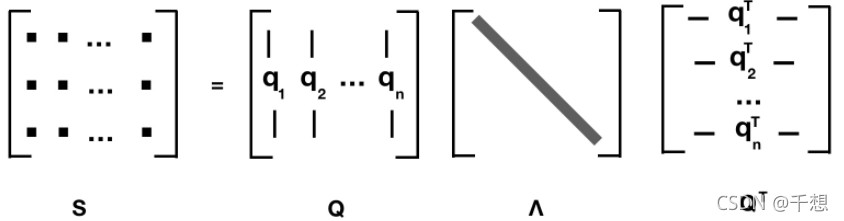
其中,S是实对称矩阵(所以自然是方阵了),Q是正交矩阵,Λ是对角矩阵;Q中是特征向量, Λ中是特征值。
3.2.1 奇异值分解(Singular Value Decomposition)
具体说明请参看参考[3]。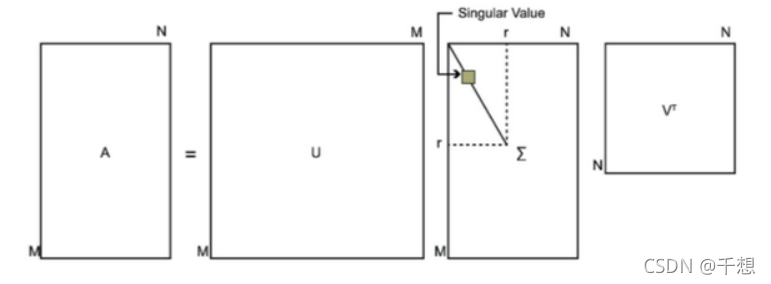
其中,A为M乘N的矩阵,U和V分别为M和N阶的方阵,∑为M乘N的除了主对角线之外全为0的矩阵。
SVD有个有趣的性质:
奇异值和特征值类似,在奇异值矩阵中也是按照从大到小排列,而且奇异值的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。
也就是说,可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。
即
A m × n = U m × m Σ m × n V n × n T ≈ U m × k Σ k × k V k × n T . A_{m \times n}=U_{m \times m} \Sigma_{m \times n} V_{n \times n}^{T} \approx U_{m \times k} \Sigma_{k \times k} V_{k \times n}^{T}.Am×n=Um×mΣm×nVn×nT≈Um×kΣk×kVk×nT.
根据这个原理就可以对矩阵进行降维。
4 其他发现
4.1 低秩矩阵分解
低秩分解是一个更加宽泛的定义,其主要包括SVD分解、Tucker分解和Block Term分解。
低秩矩阵可以理解为冗余信息较多的矩阵,比如一幅纯色图片或者图案较为规律的图片。再具体来说,就是图像矩阵可以用少数的几个基表示(这地方是不是可以先降维到如此?)。满足低秩条件的矩阵,就可以通过某些算法将原始矩阵分为低秩矩阵和噪声矩阵的加和。
即D ( 原 始 矩 阵 ) = A ( 低 秩 矩 阵 ) + E ( 稀 疏 噪 声 矩 阵 ) . D(原始矩阵)=A(低秩矩阵)+E(稀疏噪声矩阵).D(原始矩阵)=A(低秩矩阵)+E(稀疏噪声矩阵).
而分解的话可通过将其转化为凸优化问题再去求解,方法有迭代阈值算法、加速近端梯度算法、对偶方法、增广拉格朗日乘子法等。
5 结束语
结束语部分写一下整体的总结和思考。
整体知识内容和老师表达的意思都应该理解充分了。目前感觉有用的信息点就是稀疏表示和低秩矩阵分解。
稀疏表示可以将初始的遮挡图片分解为大的字典矩阵和用到的矩阵,不过这个能有效应用的前提估计是建立好较大范围的字典矩阵,这就需要已知遮挡前的众多图像,感觉又不完全符合所应用方向。
低秩矩阵分解笼统上觉得离整体方向最近,很多论文也用稀疏表示加低秩矩阵分解进行有遮挡的人脸识别问题的识别。其中,奇异值分解就是低秩矩阵分解的一种。奇异值分解的话可以进行有效且计算简单的降维,如果图像中有大量冗余信息,那么经过降维之后再进行模式识别会不会有好的进展?或者说有遮挡部分的图片经过降维后可以清晰的找出,比如平常是五维的,遮挡后其中一维表现不出来就是四维的了。但并不完全确定。
目前看到的几篇类似的文章是有这么用的,但是看起来效果一般,不知道是不是正确的方向。
参考文献
[1] https://blog.csdn.net/Forever_pupils/article/details/88572281
[2] https://zhuanlan.zhihu.com/p/97923419
[3] https://zhuanlan.zhihu.com/p/29846048