题目:请从字符串中找出一个最长的不包含重复字符的子字符串,计算该最长子字符串的长度。
示例 1:
输入: "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
输入: "bbbbb"
输出: 1
解释:因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3:
输入: "pwwkew"
输出: 3
解释:因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
提示: s.length <= 40000
解题思路:动态规划
长度为N的字符串共有 (1+N)N\2个子字符串(复杂度为O(N2),判断长为N的字符串是否有重复字符的复杂度为O(N),因此本题使用暴力解决法的复杂度为O(N3)。考虑使用动态规划降低时间复杂度。
动态规划解析:
- 状态定义:设动态规划列表 dp ,dp[ j ] 代表以字符 s[ j ] 为结尾的 “最长不重复子字符串” 的长度。
- 转移方程: 固定右边界 j ,设字符 s[ j ] 左边距离最近的相同字符为 s[ i ] ,即 s[ i ] = s[ j ] 。
- 当 i < 0 ,即 s[ j ] 左边无相同字符,则 dp[ j ] = dp[ j - 1 ] + 1 ;
当 dp[ j - 1] < j - i ,说明字符 s[ i ] 在子字符串 dp[ j - 1 ] 区间之外 ,则 dp[ j ] = dp[ j - 1 ] + 1;
当 dp[ j − 1 ] ≥ j − i ,说明字符 s[ i ] 在子字符串 dp[ j - 1 ] 区间之中 ,则 dp[ j ] 的左边界由 s[ i ] 决定,即 dp[ j ] = j - i ;
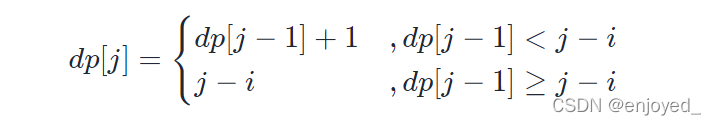
- 返回值:max( dp ) ,即全局的 “最长不重复子字符串” 的长度。
方法一:动态规划+哈希表
- 哈希表统计:遍历字符串 s 时,使用哈希表(记为 dic )统计各字符最后一次出现的索引位置 。
- 左边界 i 获取方式:遍历到 s[ j ] 时,可通过访问哈希表 dic[ s[ j ] ] 获取最近的相同字符的索引 i 。
class Solution {
public int lengthOfLongestSubstring(String s) {
Map<Character, Integer> dic = new HashMap<>();
int res = 0, tmp = 0;
for(int j = 0; j < s.length(); j++) {
int i = dic.getOrDefault(s.charAt(j), -1); // 获取索引 i
dic.put(s.charAt(j), j); // 更新哈希表
tmp = tmp < j - i ? tmp + 1 : j - i; // dp[j - 1] -> dp[j]
res = Math.max(res, tmp); // max(dp[j - 1], dp[j])
}
return res;
}
}方法二:动态规划 + 线性遍历
- 左边界 i 获取方式:遍历到 s[ j ] 时,初始化索引 i = j - 1 ,向左遍历搜索第一个满足 s[ i ] = s[ j ] 的字符即可。
class Solution {
public int lengthOfLongestSubstring(String s) {
Map<Character, Integer> dic = new HashMap<>();
int res = 0, tmp = 0;
for(int j = 0; j < s.length(); j++) {
int i = j - 1;
while(i >= 0 && s.charAt(i) != s.charAt(j)) i--; // 线性查找 i
tmp = tmp < j - i ? tmp + 1 : j - i; // dp[j - 1] -> dp[j]
res = Math.max(res, tmp); // max(dp[j - 1], dp[j])
}
return res;
}
}