空间描述和变换

1、位姿描述：即操作臂的位置和状态。

2、坐标系一般变换：

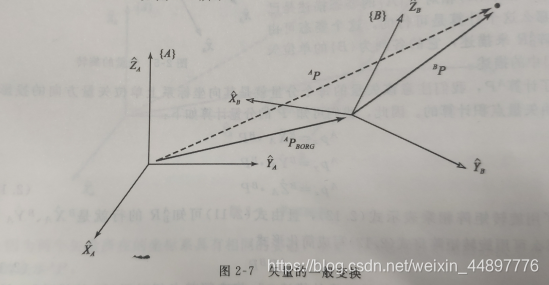
表示B相对于A的坐标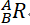
表示B坐标系的原点偏距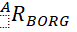

3、复合变换和逆变换

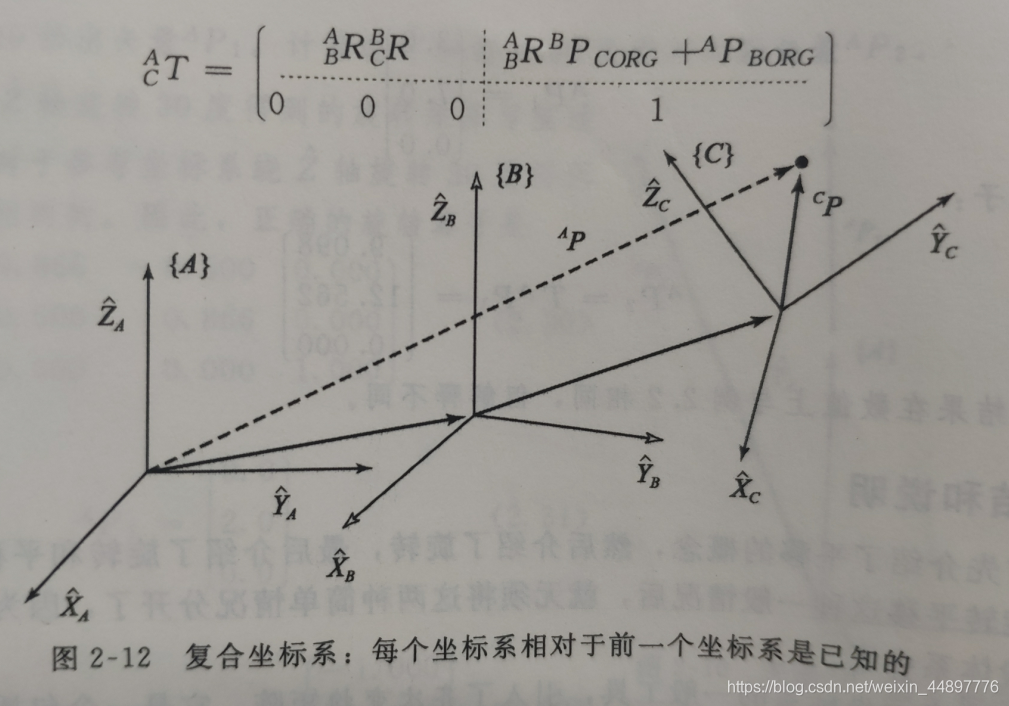
4、其他姿态描述

X-Y-Z固定角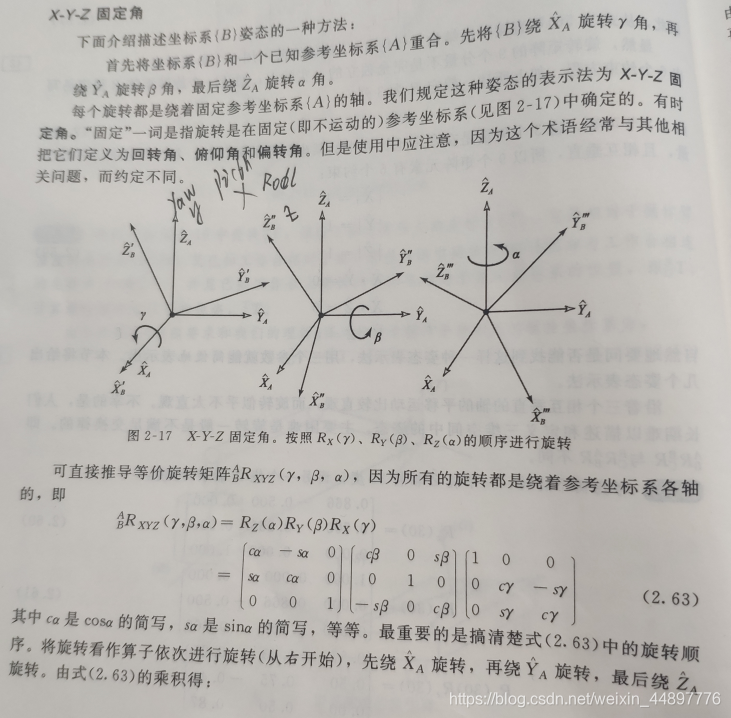

Z-Y-X（z-y-z）欧拉角
首先将坐标系{B}和另一个已知参考坐标系{A}重合。先将{B}绕Zb转α角，再绕Yb转β角，最后绕Xb转γ角。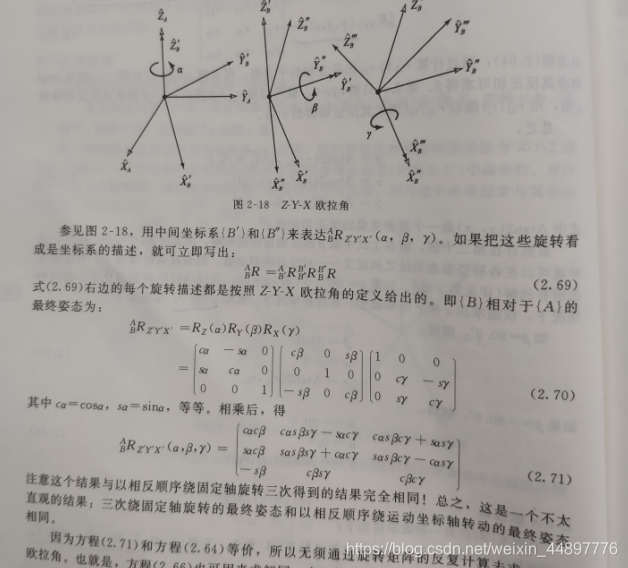

等效角度-轴线表示法
符号Rx(30.0)表示绕一个给定轴X旋转30度的姿态描述。

P43页MATLAB练习

1.a

注意
用 a,b,c分别代表角α，β，γ 。
我用的是角度，sind(角度)

clc
clear all
  
a=input("输入欧拉角a：");%a-alpha,b-beta,c-gramma
b=input("输入欧拉角b：");
c=input("输入欧拉角c：");
                          
Rz=[cosd(a), -sind(a), 0; sind(a), cosd(a), 0; 0, 0, 1]; %afa是绕z轴旋转a，偏航角——yaw
Ry=[cosd(b),0, sind(b);0, 1, 0; -sind(b), 0, cosd(b)];%beta是绕y轴旋转b，俯仰角——pitch
Rx=[1, 0, 0; 0, cosd(c), -sind(c); 0, sind(c), cosd(c)];%gama是绕x轴旋转c，翻滚角——roll

R=Rz*Ry*Rx;   
R 


  

运行程序，例如输入角度45,45,45，得到旋转矩阵R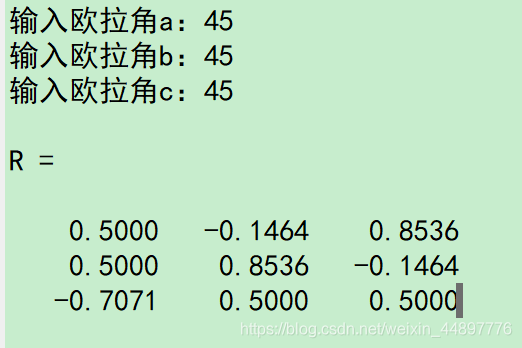

1.b

clc
clear all


a=input("输入欧拉角a：");%a-alpha,b-beta,c-gramma
b=input("输入欧拉角b：");
c=input("输入欧拉角c：");
Rz=[cosd(a), -sind(a), 0; sind(a), cosd(a), 0; 0, 0, 1]; %afa是绕z轴旋转a，偏航角——yaw
Ry=[cosd(b),0, sind(b);0, 1, 0; -sind(b), 0, cosd(b)];%beta是绕y轴旋转b，俯仰角——pitch
Rx=[1, 0, 0; 0, cosd(c), -sind(c); 0, sind(c), cosd(c)];%gama是绕x轴旋转c，翻滚角——roll

R=Rz*Ry*Rx;    


b=(atan(-R(3,1)/sqrt(R(1,1)^2+R(2,1)^2)))*180/pi;
a=(atan((R(2,1)/cosd(b))/(R(1,1)/cosd(b))))*180/pi;
c=(atan((R(3,2)/cosd(b))/(R(3,3)/cosd(b))))*180/pi;


if b==90
    a=0;
    b=90;
    c=(atan(R(1,2)/R(2,2)))*180/pi;
    
else
    if b==-90
        a=0;
        b=-90;
        c=(-atan(R(1,2)/R(2,2)))*180/pi;
            
   end
end

a
b
c

运行程序：发现成功反解旋转矩阵

1.d

clc;
clear all;

R=rotx(pi/4)*roty(pi/4)*rotz(pi/4);

t=rpy2tr(pi/4,pi/4,pi/4);%求旋转矩阵
w=(tr2rpy(t))*180/pi;%旋转矩阵反解

R
t
w

t的第四行和第四列表示原点偏移为0.

注意：使用函数rpy2tr()反解旋转函数时可能会有不同结果，因为有序旋转顺序的存在，故旋转矩阵的反解会有多种。详情请看：https://www.cnblogs.com/dadidelearning/p/9571101.html