三、线性回归
- 构建简单的人工数据集
%matplotlib inline
import torch
from IPython import display
from matplotlib import pyplot as plt
import numpy as np
import random
num_inputs = 2 #输入特征数为2
num_examples = 1000 #训练数据集样本数
true_w = [2, -3.4] #使⽤线性回归模型真实权重
true_b = 4.2 #使⽤线性回归模型真实偏差
## 设置输入样本的特征值,在0与1之间
features = torch.from_numpy(np.random.normal(0, 1, (num_examples,num_inputs)))
## 根据真实特征值计算真实标签
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] +true_b
## 为真实标签添加噪声,噪声项服从均值为0、标准差为0.01的正态分布。
labels += torch.from_numpy(np.random.normal(0, 0.01,
size=labels.size()))
print(features[:])
提示:python中numpy.random.normal(loc=0,scale,size=shape) ,意义如下:
参数loc(float):正态分布的均值,对应着这个分布的中心。loc=0说明这一个以Y轴为对称轴的正态分布,
参数scale(float):正态分布的标准差,对应分布的宽度,scale越大,正态分布的曲线越矮胖,scale越小,曲线越高瘦。
参数size(int 或者整数元组):输出的值赋在shape里,默认为None。
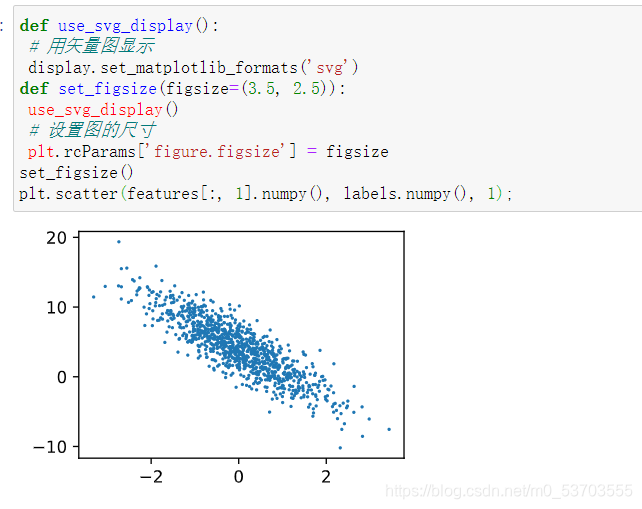
matplotlib中plt.scatter()参数详解
scatter(x, y, s=None, c=None, marker=None, cmap=None, norm=None,
vmin=None, vmax=None, alpha=None, linewidths=None, verts=None,
edgecolors=None, hold=None, data=None, **kwargs) 只解释前三个:
x,y:输入数据,array_like,shape(n,)
s:点的大小:标量或array_like,shape(n,),可选 大小以点数^ 2。默认是rcParams ['lines.markersize'] ** 2。读取数据 在训练模型的时候,我们需要遍历数据集并不断读取⼩批量数据样本。这⾥我们定义⼀个函数,它每次返回 batch_size(批量⼤⼩)个随机样本的特征和标签。
def data_iter(batch_size, features, labels):
num_examples = len(features)
indices = list(range(num_examples))
random.shuffle(indices) # 样本的读取顺序是随机的
for i in range(0, num_examples, batch_size):
j = torch.LongTensor(indices[i: min(i + batch_size,
num_examples)]) # 最后⼀次可能不⾜⼀个batch
yield features.index_select(0, j), labels.index_select(0,
j)
#让我们读取第⼀个⼩批量数据样本并打印。每个批量的特征形状为(10, 2),分别对应批量⼤⼩和输⼊个数;标签形状为批量⼤⼩。
batch_size = 10
for X, y in data_iter(batch_size, features, labels):
print(X, y)
break
#输出结果为tensor([[-1.4239, -1.3788],
[ 0.0275, 1.3550],
[ 0.7616, -1.1384],
[ 0.2967, -0.1162],
[ 0.0822, 2.0826],
[-0.6343, -0.7222],
[ 0.4282, 0.0235],
[ 1.4056, 0.3506],
[-0.6496, -0.5202],
[-0.3969, -0.9951]])
tensor([ 6.0394, -0.3365, 9.5882, 5.1810, -2.7355, 5.3873,
4.9827, 5.7962,4.6727, 6.7921])
- 初始化模型参数
将权重初始化成均值为0、标准差为0.01的正态随机数,偏差则初始化成0。
w = torch.tensor(np.random.normal(0, 0.01, (num_inputs, 1)),
dtype=torch.float64)
b = torch.zeros(1, dtype=torch.float64)
#之后的模型训练中,需要对这些参数求梯度来迭代参数的值,因此我们要让它们的requires_grad=True
w.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)
- 定义模型
下⾯是线性回归的⽮量计算表达式的实现。我们使⽤ mm 函数做矩阵乘法
def linreg(X, w, b):
return torch.mm(X, w) + b
- 定义损失函数
使⽤上面描述的平⽅损失来定义线性回归的损失函数。在实现中,我们需要把真实值 y 变形成预测值 y_hat 的形状。以下函数返回的结果也将和 y_hat 的形状相同。
def squared_loss(y_hat, y):
# 注意这⾥返回的是向量, 另外, pytorch⾥的MSELoss并没有除以 2
return (y_hat - y.view(y_hat.size())) ** 2 / 2
- 定义优化算法
以下的 sgd 函数实现了上⼀节中介绍的⼩批量随机梯度下降算法。它通过不断迭代模型参数来优化损失函数。这⾥⾃动求梯度模块计算得来的梯度是⼀个批量样本的梯度和。我们将它除以批量⼤⼩来得到平均值。
def sgd(params, lr, batch_size):
for param in params:
param.data -= lr * param.grad / batch_size # 注意这⾥更改param时⽤的param.data
- 训练模型
在训练中,我们将多次迭代模型参数。在每次迭代中,我们根据当前读取的⼩批量数据样本(特征 X 和标签 y ),通过调⽤反向函数 backward 计算⼩批量随机梯度,并调⽤优化算法 sgd 迭代模型参数。由于我们之前设批量⼤⼩ batch_size 为10,每个⼩批量的损失 l 的形状为(10, 1)。回忆⼀下⾃动求梯度那里。由于变量 l 并不是⼀个标量,所以我们可以调⽤ .sum() 将其求和得到⼀个标量,再运⾏ l.backward() 得到该变量有关模型参数的梯度。注意在每次更新完参数后不要忘了将参数的梯度清零。
lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss
for epoch in range(num_epochs): # 训练模型⼀共需要num_epochs个迭代周期
# 在每⼀个迭代周期中,会使⽤训练数据集中所有样本⼀次(假设样本数能够被批量⼤⼩整除)。X和y分别是⼩批量样本的特征和标签
for X, y in data_iter(batch_size, features, labels):
l = loss(net(X, w, b), y).sum() # l是有关⼩批量X和y的损失
l.backward() # ⼩批量的损失对模型参数求梯度
sgd([w, b], lr, batch_size) # 使⽤⼩批量随机梯度下降迭代模型参数
# 不要忘了梯度清零
w.grad.data.zero_()
b.grad.data.zero_()
train_l = loss(net(features, w, b), labels)
print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))
在⼀个迭代周期(epoch)中,我们将完整遍历⼀遍 data_iter 函数,并对训练数据集中所有样本都使⽤⼀次(假设样本数能够被批量⼤⼩整除)。这⾥的迭代周期个数 num_epochs 和学习率 lr 都是超参数,分别设3和0.03。在实践中,⼤多超参数都需要通过反复试错来不断调节。虽然迭代周期数设得
越⼤模型可能越有效,但是训练时间可能过⻓。⽽有关学习率对模型的影响。
小结:从零到训练一个模型的步骤如下
准备数据集→遍历数据集并不断读取⼩批量数据样本→初始化模型参数→定义模型→定义损失函数→定义优化算法(调参)→训练模型。
四、线性回归的简洁实现
- 介绍如何使⽤PyTorch更⽅便地实现线性回归的训练。
torch.utils.data 模块提供了有关数据处理的⼯具,torch.nn 模块定义了⼤量神经⽹络的层, torch.nn.init 模块定义了各种初始化⽅法, torch.optim 模块提供了模型参数初始化的各种⽅法。 - 生成数据集
%matplotlib inline
import torch
from IPython import display
from matplotlib import pyplot as plt
import numpy as np
import random
#其中 features 是训练数据特征, labels 是标签。
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = torch.tensor(np.random.normal(0, 1, (num_examples,
num_inputs)), dtype=torch.float)
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += torch.tensor(np.random.normal(0, 0.01,size=labels.size()), dtype=torch.float)
读取数据
PyTorch提供了 data 包来读取数据。由于 data 常⽤作变量名,那么导⼊的 data 模块⽤ Data代替。在每⼀次迭代中,我们将随机读取包含10个数据样本的⼩批量。
import torch.utils.data as Data
batch_size = 10
# 将训练数据的特征和标签组合
dataset = Data.TensorDataset(features, labels)
# 随机读取⼩批量
data_iter = Data.DataLoader(dataset, batch_size, shuffle=True)
#这⾥ data_iter 的使⽤跟上⼀节中的⼀样。让我们读取并打印第⼀个⼩批量数据样本。
for X, y in data_iter:
print(X, y)
break
- 定义模型
⾸先,导⼊ torch.nn 模块。实际上,“nn”是neural networks(神经⽹络)的缩写。该模块定义了⼤量神经⽹络的层。之前我们已经⽤过了 autograd ,⽽ nn 就是利⽤ autograd 来定义模型。 nn 的核⼼数据结构是 Module ,它是⼀个抽象概念,既可以表示神经⽹络中的某个层(layer)也可以表示⼀个包含很多层的神经⽹络。在实际使⽤中,最常⻅的做法是继承 nn.Module ,撰写⾃⼰的⽹络/层。⼀个 nn.Module 实例应该包含⼀些层以及返回输出的前向传播(forward)⽅法。下⾯先来看看如何⽤ nn.Module 实现⼀个线性回归模型。
class LinearNet(nn.Module):
def __init__(self, n_feature):
super(LinearNet, self).__init__()
self.linear = nn.Linear(n_feature, 1)
# forward 定义前向传播
def forward(self, x):
y = self.linear(x)
return y
net = LinearNet(num_inputs)
print(net) # 使⽤print可以打印出⽹络的结构
#输出结果如下:表示网络的第一层结构
LinearNet(
(linear): Linear(in_features=2, out_features=1, bias=True)
)
事实上我们还可以⽤ nn.Sequential 来更加⽅便地搭建⽹络, Sequential 是⼀个有序的容器,⽹络层将按照在传⼊ Sequential 的顺序依次被添加到计算图中。
# 写法⼀
net = nn.Sequential(
nn.Linear(num_inputs, 1)
# 此处还可以传⼊其他层
)
# 写法⼆
net = nn.Sequential()
net.add_module('linear', nn.Linear(num_inputs, 1))
# net.add_module ......
# 写法三
from collections import OrderedDict
net = nn.Sequential(OrderedDict([
('linear', nn.Linear(num_inputs, 1))
# ......
]))
print(net)
print(net[0])
#输出结果如下:
Sequential(
(linear): Linear(in_features=2, out_features=1, bias=True)
)
Linear(in_features=2, out_features=1, bias=True)
可以通过 net.parameters() 来查看模型所有的可学习参数,此函数将返回⼀个⽣成器。
for param in net.parameters():
print(param)
#输出结果如下:
Parameter containing:
tensor([[-0.0277, 0.2771]], requires_grad=True)
Parameter containing:
tensor([0.3395], requires_grad=True)
- 初始化模型参数
在使⽤ net 前,我们需要初始化模型参数,如线性回归模型中的权᯿和偏差。PyTorch在 init 模块中 提供了多种参数初始化⽅法。这⾥的 init 是 initializer 的缩写形式。我们通过 init.normal_ 将权重参数每个元素初始化为随机采样于均值为0、标准差为0.01的正态分布。偏差会初始化为零。
from torch.nn import init
init.normal_(net[0].weight, mean=0, std=0.01)
init.constant_(net[0].bias, val=0) # 也可以直接修改bias的data:net[0].bias.data.fill_(0)
- 定义损失函数
PyTorch在 nn 模块中提供了各种损失函数,这些损失函数可看作是⼀种特殊的层,PyTorch也将这些损失函数实现为 nn.Module 的⼦类。这里使⽤它提供的均⽅误差损失作为模型的损失函数。
loss = nn.MSELoss()
- 定义优化算法
⽆须⾃⼰实现⼩批量随机梯度下降算法。 torch.optim 模块提供了很多常⽤的优化算法⽐如SGD、Adam和RMSProp等。下⾯我们创建⼀个⽤于优化 net 所有参数的优化器实例,并指定学习率为0.03的⼩批量随机梯度下(SGD)为优化算法。
import torch.optim as optim
optimizer = optim.SGD(net.parameters(), lr=0.03)
print(optimizer)
还可以为不同⼦⽹络设置不同的学习率
optimizer =optim.SGD([
# 如果对某个参数不指定学习率,就使⽤最外层的默认学习率
{'params': net.subnet1.parameters()}, # lr=0.03
{'params': net.subnet2.parameters(), 'lr': 0.01}
], lr=0.03)
注意,使用书中的代码运行时会报错。这是因为subnet1、subnet2 指是己定义的网络名字,就比如net.add_module(‘linear’, nn.Linear(num_inputs, 1)),只有一层,所以subnet1其实就是linear,写成net.linear.parameters(),如果你再加入一层命名为linear1,就写作net.linear1.parameters()
- 训练模型
在使⽤Gluon训练模型时,通过调⽤ optim 实例的 step 函数来迭代模型参数。按照⼩批量随机梯度下降的定义,在 step 函数中指明批量⼤⼩,从⽽对批量中样本梯度求平均。
num_epochs = 3
for epoch in range(1, num_epochs + 1):
for X, y in data_iter:
output = net(X)
l = loss(output, y.view(-1, 1))
optimizer.zero_grad() # 梯度清零,等价于net.zero_grad()
l.backward()
optimizer.step()
print('epoch %d, loss: %f' % (epoch, l.item()))