1、关联分析的基本概念
关联分析(association analysis):从大规模数据集中寻找物品间的隐含关系。
项集(itemset):包含0个或者多个项的集合称为项集。
频繁项集:那些经常一起出现的物品集合
支持度(support):一个项集的支持度被定义为数据集中包含该项集的记录所占的比例。
可信度(confident):是针对一条诸如{尿布}→{啤酒}的关联规则来定义的。
可信度({尿布}→{啤酒})=支持度({尿布,啤酒})/支持度({尿布})
关联规则是形如A->B的表达式,规则A->B的度量包括支持度和置信度
项集支持度:一个项集出现的次数与数据集所有事物数的百分比称为项集的支持度
eg: support(A->B) = support_count(A∪B) / N
支持度反映了A和B同时出现的概率,关联规则的支持度等于频繁集的支持度。
项集置信度:数据集中同时包含A、B的百分比
eg: confidence(A->B) = support_count(A∪B) / support_count(A)
可信度反映了如果交易中包含A,则交易包含B的概率。也可以称为在A发生的条件下,发生B的概率,成为条件概率。
只有支持度和可信度较高的关联规则才是用户感兴趣的。
关联分析的两种关系:简单关联关系和序列关联关系
简单关联关系:
简单关联关系可以从经典的购物中进行分析,购买面包的顾客80%都会购买牛奶,由于面包和牛奶是早餐搭配的必需品,二者搭配构成了早餐的组成部分,这就是一种简单的关联关系。
序列关联关系:
当购买一款新手机后,就会考虑去购买手机膜等手机配件,这就是一种序列关系,不会先买手机膜再买手机的,先后关系是非常明显的,这种关系是一种顺序性的关系,也就是一种序列关联关系。
关联规则:规则就是一种衡量事物的标准,也就是一个算法。
关联规则同样的可以分为两种:简单关联规则和序列关联规则
简单关联规则:
简单关联规则是无指导的学习方法,着重探索内部结构。简单关联规则也是使用最多的技术,主要算法包括:Apriori、GRI、Carma,其中Apriori和Carma主要是如何提高关联规则的分析效率,而GRI注重如何将单一概念层次的关联推广到更多概念层次的关联,进而揭示事物内在结构。
简单关联规则的数据存储形式:一种是交易数据格式,一种是表格数据格式。
序列关联规则:
序列关联规则的核心就是找到事物发展的前后关联性,研究序列关联可以来推测事物未来的发展情况,并根据预测的发展情况进行事物的分配和安排。
关联分析的应用:
(1):购物篮分析,通过查看那些商品经常在一起出售,可以帮助商店了解用户的购物行为,这种从数据的海洋中抽取只是可以用于商品定价、市场促销、存货管理等环节
(2):在Twitter源中发现一些公共词。对于给定的搜索词,发现推文中频繁出现的单词集合
(3):从新闻网站点击流中挖掘新闻流行趋势,挖掘哪些新闻广泛被用户浏览到
(4):搜索引擎推荐,在用户输入查询时推荐同时相关的查询词项
(5):发现毒蘑菇的相似特征。这里只对包含某个特征元素(有毒素)的项集感兴趣,从中寻找毒蘑菇中的一些公共特征,利用这些特征来避免迟到哪些有毒的蘑菇
(6):图书馆信息的书籍推荐,对于学生的借书信息,不同专业学生的借书情况,来挖掘不同学生的借书情况,进行数目的推荐。
(7):校园网新闻通知信息的推荐,在对校园网新闻通知信息进行挖掘的过程中,分析不同部门,不同学院的新闻信息的不同,在进行新闻信息浏览的过程中进行新闻的推荐。
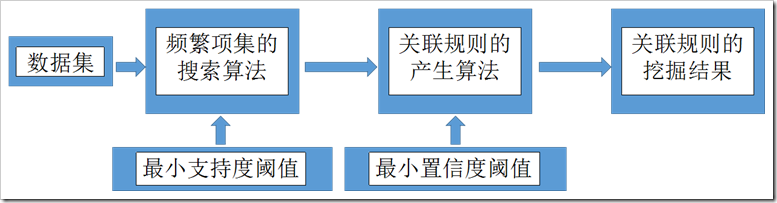
关联规则挖掘的步骤:
(1)找出存在于数据集中的所有频繁项集,即找出那些支持度不小于事先给定的支持度阈值的项集。
(2)在频繁项集的基础上产生强关联规则,即产生那些支持度和置信度分别大于或等于事先给定的支持度阈值和置信度阈值的关联规则。
从频繁项集到强关联规则:
支持度和置信度是描述关联规则的两个重要概念;
支持度用于衡量关联规则在整个数据集中的统计重要性,置信度用于衡量关联规则的可信程度;
所有支持度大于最小支持度的项集称为频繁项集,关联规则由频繁项集产生。同时满足最小支持度闭值和最小置信度闭值的规则称为强规则,约束规则是在强规则的基础上提取的符合条件的规则。
如何设定合理的支持度和置信度?
对于某条规则:(A=a)->(B=b)(support=30%,confident=60%);其中support=30%表示在所有的数据记录中,同时出现A=a和B=b的概率为30%;confident=60%表示在所有的数据记录中,在出现A=a的情况下出现B=b的概率为60%,也就是条件概率。支持度揭示了A=a和B=b同时出现的概率,置信度揭示了当A=a出现时,B=b是否会一定出现的概率。
(1)如果支持度和置信度闭值设置的过高,虽然可以减少挖掘时间,但是容易造成一些隐含在数据中非频繁特征项被忽略掉,难以发现足够有用的规则;
(2)如果支持度和置信度闭值设置的过低,又有可能产生过多的规则,甚至产生大量冗余和无效的规则,同时由于算法存在的固有问题,会导致高负荷的计算量,大大增加挖掘时间。
2、算法的基本原理
经典的关联规则挖掘算法包括Apriori算法和FP-growth算法,前者多次扫描数据库,每次利用候选频繁集产生频繁集;后者则利用树形结构直接得到频繁集,减少了扫描数据库的次数,从而提高了算法的效率。但是,前者的扩展性较好,可用于并行计算等领域。
Apriori算法
Apriori算法是挖掘布尔型关联规则频繁项集的最为经典、最为基础的算法,该算法需要不断寻找候选集,然后剪枝即去掉非频繁子集的候选集,时间复杂度由暴力枚举所有子集的指数级别O(n2)将为多项式级别,多项式具体系数是底层实现情况而定的。
Apriori算法基于这样的事实:算法使用频繁项集的性质的先验知识。Apriori使用一种称作逐层搜索的迭代方法,k-项集用于探索(k+1)-项集。首先,找出频繁1-项集的集合。该集合记作L1。L1用于找频繁2-项集的集合L2,而L2用于找L3,如此下去,直到不能找到频繁k-项集。Ariori算法有两个主要步骤:
1、连接:(将项集进行两两连接)
利用已经找到的Lk,通过两两连接得出C(k+1),注意进行连接的Lk[i],Lk[j],必须有k-1个属性值相同,然后另外两个不同的分别分布在Lk[i],Lk[j],这样的求出的C(k+1)为L(k+1)的候选集。
2、剪枝:(去掉非频繁项集)
候选集 Ck+1中的并不都是频繁项集,必须剪枝去掉,越早越好以防止所处理的数据无效项越来越多。只有当子集都是频繁集的候选集才是频繁集,这是剪枝的依据.

3、算法实现
# -*- coding:utf-8 -*-
import itertools
import copy
'''
定义全局变量k,即支持度计数k,此k也可以在运行程序之前输入,简单改动即可
'''
k = 2
'''
存储频繁项集的列表
'''
frequenceItem = []
'''
从txt文件dataset.txt里获取事务集
'''
def getDataSet(args):
f = open(args, 'r')
source = f.readlines()
f.close()
dataset = []
for line in source:
temp1 = line.strip('\r\n')
temp2 = temp1.split(',')
dataset.append(temp2)
return dataset
'''
初步扫描事务集,从事务集里获取候选1项集
方法的基本思路是:
定义一个集合tmp,将事务集的第一项作为tmp的初始集合
然后扫描事务集,将不在tmp里的数据项加入tmp中
'''
def find_item(dataset):
length = len(dataset)
for i in range(0, length):
if i == 0:
tmp = set(dataset[i])
tmp.update(set(dataset[i]))
candidate = list(tmp)
candidate.sort()
return candidate
'''
从候选项集里找出频繁项集,其中num代表频繁num+1项集
如num为0的为从候选1项集里找出频繁1项集
方法基本思路:
1、定义一个支持度列表count
2、对于每一个候选项,依次扫描事务集,如果该项出现在事务集中就将该项对应的count+1、定义一个支持度列表count+1
3、将每一项的count和k(支持度计数)进行比较,将count小于k的项剔除
'''
'''
其实不管num为0还是别的值算法应该是一样的,但是由于程序实现上的问题
num为0的时候选项集是一维列表,其它的时候,候选项集是二维列表,
毕竟只是自己写着玩的,python还不熟,牵一发而动全身,懒得改了
'''
def find_frequent(candidate, dataset, num):
frequence = []
length = len(candidate)
count = []
for i in range(0, length):
count.append(0)
count[i] = 0
if num == 0:
child = set([candidate[i]])
else:
child = set(candidate[i])
for j in dataset:
parent = set(j)
if child.issubset(parent):
count[i] = count[i] + 1
for m in range(0, length):
if count[m] >= k:
frequence.append(candidate[m])
return frequence
'''
先验定理,剪枝掉不必要的候选n项集
方法思路:
1、依次取出候选项集里的项
2、取出n项集里的n-1项子集
3、如果所有的n-1项集不都都是频繁n-1项集的子集,则删除该候选项集
'''
def pre_test(candidate, num, frequence):
r_candidate = copy.deepcopy(candidate)
for each in candidate:
for each2 in itertools.combinations(each, num):
tmp = (list(each2))
tag = 0
for j in frequence:
if num == 1:
if (tmp[0] == j):
tag = 1
break
else:
if tmp == j:
tag = 1
break
if tag == 0:
r_candidate.remove(each)
break
return r_candidate
'''
通过频繁n-1项集产生候选n项集,并通过先验定理对候选n项集进行剪枝
方法思路:
1、如果是频繁1项集,则通过笛卡尔积产生频繁2项集
2、如果不是频繁一项集,采用F(k-1) * F(k-1)方法通过频繁n-1项集产生候选n项集
注:F(k-1) * F(k-1)方法在我的另一篇关联算法博客上做了理论上的简单介绍,或者也可以直接参看《数据挖掘导论》
'''
def get_candidata(frequence, num):
length = len(frequence)
candidate = []
if num == 1:
for each in itertools.combinations(frequence, 2):
tmp = list(each)
tmp3 = []
tmp3.append(tmp[0])
tmp3.append(tmp[1])
candidate.append(tmp3)
else:
for i in range(0, length - 1):
tmp1 = copy.deepcopy(frequence[i])
tmp1.pop(num - 1)
for j in range(i + 1, length):
tmp2 = copy.deepcopy(frequence[j])
tmp2.pop(num - 1)
if tmp1 == tmp2:
tmp3 = copy.deepcopy(frequence[i])
tmp3.append(frequence[j][num - 1])
candidate.append(tmp3)
candidate2 = pre_test(candidate, num, frequence)
return candidate2
'''
main程序
'''
if __name__ == '__main__':
dataset = getDataSet('dataset.txt')
Item = find_item(dataset)
num = 0
frequenceItem = []
'''
通过事务集找到频繁项集,直至频繁n项集为空,则退出循环
'''
while 1:
if num == 0:
candidate = Item
else:
candidate = get_candidata(frequenceItem[num - 1], num)
frequenceItem.append(find_frequent(candidate, dataset, num))
if frequenceItem[num] == []:
frequenceItem.pop(num)
break
num = num + 1
'''
打印出频繁项集
'''
for each in frequenceItem:
print each4、总结算法特点,应用范围等等
关联规则挖掘要求输入的数据必须为布尔型,而推荐系统并处理的评价或喜好值多为数值型的。由于数据类型不是二值布尔型,无法应用关联规则挖掘算法找出项目之间的关联。典型的做法就是先将评价值离散化。常用的自动离散化方法包括分箱、直方图分析、基于熵的离散化、基于统计分析离散化、聚类分析和根据直观划分离散化。
离散化方法:先计算某项目qn的平均评分Q,接着遍历每位用户对qn的评分,如果大于Q,则标记为1,否则标记为0.
参考:
【2】http://www.tuicool.com/articles/N3UB3m

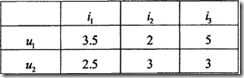
 关联规则推荐算法示例数据
关联规则推荐算法示例数据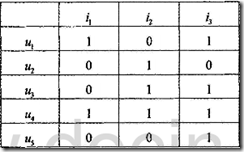 离散化后的关联规则推荐算法示例数据
离散化后的关联规则推荐算法示例数据