写在前面
前段时间看了一下ESKF的相关知识,VIO中(VINS)用的还是挺多的,特此总结
先验知识——四元数
- 四元数的基本表示形式,这个还是蛮重要的,主要有以下几种表示形式
- Q = a + b i + c j + d k Q=a+bi+cj+dkQ=a+bi+cj+dk
- q = q w + q ‾ v q=q_w+\overline q_vq=qw+qv
- q = [ q w q v ] q=\begin{bmatrix} q_w \\ q_v \end{bmatrix}q=[qwqv]
四元数的乘法运算,四元数的运算可以写作矩阵运算的形式,具体形式如下:
q 1 ⊗ q 2 = [ q 1 ] L q 2 q_1 \otimes q_2=[q_1]_Lq_2q1⊗q2=[q1]Lq2 或者 q 1 ⊗ q 2 = [ q 2 ] R q 1 q_1 \otimes q_2=[q_2]_Rq_1q1⊗q2=[q2]Rq1
其中每个矩阵的形式如下
[ q ] L = q w I + [ 0 − q v T q v [ q v ] × ] [ q ] R = q w I + [ 0 − q v T q v − [ q v ] × ] [q]_L=q_wI+\begin{bmatrix} 0 \quad -q_v^T \\ q_v \quad [q_v]_× \end{bmatrix} \\ [q]_R=q_wI+\begin{bmatrix} 0 \quad -q_v^T \\ q_v \quad -[q_v]_× \end{bmatrix}[q]L=qwI+[0−qvTqv[qv]×][q]R=qwI+[0−qvTqv−[qv]×]
应该特别注意到!!!上面两种方式只有一处不同,瞬间解放了多少大脑细胞(虽然根本就不记^_^)
同时也可以将上面的内容写作
p ⊗ q = [ p w q w − p v T q v p w q v + q w p v + p v × q v ] p \otimes q=\begin{bmatrix}p_wq_w-p_v^Tq_v \\ p_wq_v+q_wp_v+p_v×q_v\end{bmatrix}p⊗q=[pwqw−pvTqvpwqv+qwpv+pv×qv]通过四元数的微分方程q ˙ = q ⊗ Ω \dot q=q \otimes \Omegaq˙=q⊗Ω可以看到,四元数与SO(3)一样,可以写作exp映射的形式,并且,两者的旋转向量是一样的,不过对于旋转矩阵的映射而言,首先会将旋转向量映射到so(3)上,之后SO(3)与so(3)通过exp来一一对应,而四元数是将旋转向量先映射到tangent space之后再与四元数进行exp映射
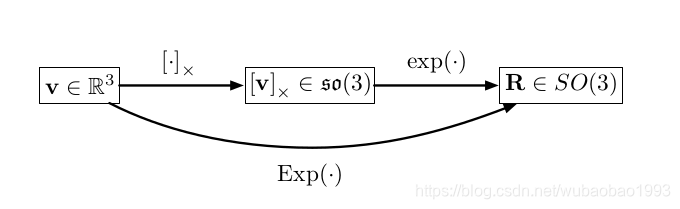
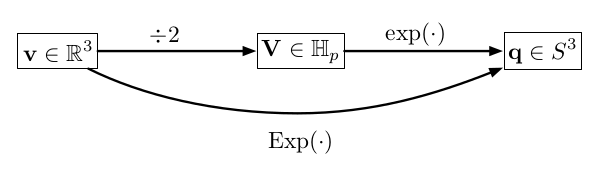
对于旋转变量而言,总能将其表示为v = φ u v=φuv=φu的形式,其中φ φφ是旋转角,u uu是旋转轴,可以通过下面的图来表示,但是对于四元数而言,其旋转的角度其实只是真实旋转的一半(我们可以从r ( v ) = q × v × q ′ r(v)=q×v×q'r(v)=q×v×q′公式中看出四元数对于一个向量进行旋转的时候是要旋转两次的,因此这里一个四元数仅仅旋转半次,所以从上面的图中可以看到tangent space仅仅是旋转向量除以2得到的),因此V = φ u / 2 = θ u V=φu/2=θuV=φu/2=θu
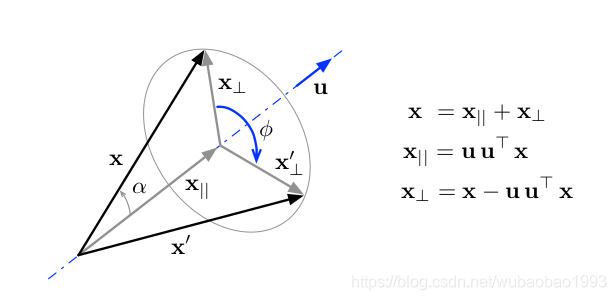
我们将V = φ u / 2 = θ u V=φu/2=θuV=φu/2=θu 带入exp进行泰勒展开之后得到
q = E x p ( ϕ u ) = e ϕ u / 2 = c o s ( ϕ / 2 ) + u s i n ( ϕ / 2 ) = [ c o s ( ϕ / 2 ) u s i n ( ϕ / 2 ) ] q=Exp(\phi u)=e^{\phi u/2}=cos(\phi/2)+usin(\phi/2)=\begin{bmatrix}cos(\phi/2) \\ usin(\phi/2)\end{bmatrix}q=Exp(ϕu)=eϕu/2=cos(ϕ/2)+usin(ϕ/2)=[cos(ϕ/2)usin(ϕ/2)]
可以看到,经过化简之后,我们就很容易通过sin和cos得到一个四元数了,更多的,如果采样频率很高,即φ φφ很小,可以得到q = [ 1 , φ u / 2 ] q=[1, φu/2]q=[1,φu/2]这样简单的四元数经过化简之后,我们就很容易通过sin和cos得到一个四元数了,更多的,如果采样频率很高,即φ φφ很小,可以得到q = [ 1 , φ u / 2 ] q=[1, φu/2]q=[1,φu/2]这样简单的四元数。
Error State Kalman Filter
首先,为什么叫做error-state KF?比如此时我们的状态变量为:[位移,姿态,速度,加速度的bias,角速度的bias],即x = [ p , q , v , b a , b g ] x=[p, q, v, ba, bg]x=[p,q,v,ba,bg],那么在整个更新的过程中,我们可以认为有一个真实的状态(truth state)x t r u t h x_{truth}xtruth,之后有一个标准的状态(normal state)x xx,该状态就是我们通过IMU的测量值且不考虑噪声和扰动得到的状态,最后我们还要计算一个误差状态(error-state)δ x δxδx。三者之间的关系为x t r u t h = x + δ x x_{truth}=x+δxxtruth=x+δx。
其次,为什么我们要计算误差状态?因为我们在标准状态x的更新过程中并没有考虑测量误差以及使用的状态的扰动,这些噪声和扰动最终都会归于误差状态δ x δxδx,随后一旦有其他传感器的量测到来的时候,我们就可以与标准状态作差得到误差状态的测量值δ x m δx_mδxm,此时就可以和更新时候的误差状态δ x δxδx之间建立滤波器并对误差状态变量进行估计。
所以,在整个滤波过程中,我们实际上修正的变量是δ x δxδx!!!这点一定要清楚。
下面列是一个实际的滤波过程:
真实的状态为:
{ p ˙ t = v t v ˙ t = R t ( a m − a b t − a n ) q ˙ t = 1 2 q t ⊗ ( w m − w b t − w n ) a ˙ b t = a w w ˙ b t = w w \begin{cases} \dot p_t=v_t \\ \dot v_t=R_t(a_m-a_{bt}-a_n) \\ \dot q_t=\frac{1}{2}q_t \otimes (w_m-w_{bt}-w_n) \\ \dot a_{bt}=a_w \\ \dot w_{bt}=w_w \end{cases}⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧p˙t=vtv˙t=Rt(am−abt−an)q˙t=21qt⊗(wm−wbt−wn)a˙bt=aww˙bt=ww
标准状态为:因为bias的值我们并不能测量出来,因此只能为0
{ p ˙ = v v ˙ = R ( a m − a b ) q ˙ = 1 2 q ⊗ ( w m − w b ) a ˙ b = 0 w ˙ b = 0 \begin{cases} \dot p=v \\ \dot v=R(a_m-a_{b}) \\ \dot q=\frac{1}{2}q \otimes (w_m-w_{b}) \\ \dot a_{b}=0 \\ \dot w_{b}=0 \end{cases}⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧p˙=vv˙=R(am−ab)q˙=21q⊗(wm−wb)a˙b=0w˙b=0
误差状态为:
{ δ p ˙ = δ v δ v ˙ = − R [ a m − a b ] × δ θ − R δ a b − R a n δ θ ˙ = [ w m − w b ] × δ θ − δ w b − w n δ a ˙ b = a w δ w ˙ b = w w \begin{cases} \delta\dot p=\delta v \\ \delta \dot v=-R[a_m-a_{b}]_×\delta \theta-R\delta a_b-Ra_n \\ \delta \dot \theta=[w_m-w_{b}]_× \delta \theta-\delta w_b-w_n\\ \delta \dot a_b=a_w \\ \delta \dot w_b=w_w \end{cases}⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧δp˙=δvδv˙=−R[am−ab]×δθ−Rδab−Ranδθ˙=[wm−wb]×δθ−δwb−wnδa˙b=awδw˙b=ww
下面我们可以重点来看一下如何进行推导的,主要的公式就是真实值=标准值+误差值
对于速度V,我们有如下关系
v ˙ + δ v ˙ = v ˙ t v ˙ = R ( a − a b ) , v ˙ t = R t ( a − a b t − a w ) \dot v+\dot{\delta v}=\dot v_t \\ \dot v=R(a-a_b),\dot v_t=R_t(a-a_{bt}-a_w)v˙+δv˙=v˙tv˙=R(a−ab),v˙t=Rt(a−abt−aw)
对于上式,其中R t = R ( I + [ δ θ ] × ) , a b t = a b + δ a b R_t=R(I+[\delta \theta]_×),a_{bt}=a_b+\delta {a_b}Rt=R(I+[δθ]×),abt=ab+δab带入上式就有:
R ( a − a b ) + δ v ˙ = R ( I + [ δ θ ] × ) ( a − a b − δ a b − a w ) R(a-a_b)+\dot{\delta v}=R(I+[\delta \theta]_×)(a-a_b-\delta {a_b}-a_w)R(a−ab)+δv˙=R(I+[δθ]×)(a−ab−δab−aw)
我们假设a m = a − a b , a n = − δ a b − a w a_m=a-a_b,a_n=-\delta{a_b}-a_wam=a−ab,an=−δab−aw
经过化简就有
δ v ˙ = − R [ a m ] × δ θ − R δ a b − R a n \dot{\delta v}=-R[a_m]_×\delta{\theta}-R\delta{a_b}-Ra_nδv˙=−R[am]×δθ−Rδab−Ran对于旋转角θ \thetaθ,同样我们有如下关系:
( q + δ q ) ˙ = q t ˙ ( q + δ q ) ˙ = q ˙ ⊗ δ q + q ⊗ δ q ˙ = 1 2 q ⊗ w ⊗ δ q + q ⊗ δ q ˙ q t ˙ = 1 2 q t ⊗ w t = 1 2 q ⊗ δ q ⊗ w t \dot{(q+\delta q)}=\dot{q_t} \\ \dot{(q+\delta q)} = \dot{q}\otimes \delta{q}+q \otimes \dot{\delta{q}}=\frac{1}{2}q\otimes w\otimes \delta{q}+q\otimes \dot{\delta{q}} \\ \dot{q_t}=\frac{1}{2}q_t \otimes w_t=\frac{1}{2}q \otimes \delta{q} \otimes w_t(q+δq)˙=qt˙(q+δq)˙=q˙⊗δq+q⊗δq˙=21q⊗w⊗δq+q⊗δq˙qt˙=21qt⊗wt=21q⊗δq⊗wt
对上面的式子进行化简(用到将四元数的乘法运算变为矩阵运算)移项:
[ w ] L δ q + 2 δ q ˙ = [ w t ] R δ q [ 0 δ θ ˙ ] = [ 0 − ( w t − w ) T − ( w t − w ) − [ w t + w ] × ] [ 1 1 2 δ θ ] [w]_L\delta{q}+2\dot{\delta{q}}=[w_t]_R\delta{q} \\ \begin{bmatrix} 0 \\ \dot{\delta{\theta}} \end{bmatrix} =\begin{bmatrix} 0 \quad -(w_t-w)^T \\ -(w_t-w) \quad -[w_t+w]_× \end{bmatrix} \begin{bmatrix} 1 \\ \frac{1}{2}\delta{\theta} \end{bmatrix}[w]Lδq+2δq˙=[wt]Rδq[0δθ˙]=[0−(wt−w)T−(wt−w)−[wt+w]×][121δθ]
如果在上式中,w = w m − w b , δ w = − δ w b − w n , w t = w + δ w w=w_m-w_b,\delta{w}=-\delta{w_b}-w_n,w_t=w+\delta{w}w=wm−wb,δw=−δwb−wn,wt=w+δw,则上式可以化简为
[ 0 δ θ ˙ ] = [ 0 − δ w T − δ w − [ 2 w ] × − [ δ w ] × ] [ 1 1 2 δ θ ] \begin{bmatrix} 0 \\ \dot{\delta{\theta}} \end{bmatrix} =\begin{bmatrix} 0 \quad -\delta{w}^T \\ -\delta{w} \quad -[2w]_× -[\delta{w}]_×\end{bmatrix} \begin{bmatrix} 1 \\ \frac{1}{2}\delta{\theta} \end{bmatrix}[0δθ˙]=[0−δwT−δw−[2w]×−[δw]×][121δθ]
上面公式展开之后,忽略极小项,就可以得到下面的公式:
δ θ ˙ = − [ w ] × δ θ − δ w b − w n \dot{\delta{\theta}}=-[w]_×\delta{\theta}-\delta{w_b}-w_nδθ˙=−[w]×δθ−δwb−wn
经过上述的操作之后,我们就得到了误差状态δ x \delta{x}δx的微分方程了,随后其实就是一阶展开得到状态的更新方程
δ x = δ x + δ x ˙ = ( I + F Δ t ) δ x \delta{x}=\delta{x}+\dot{\delta{x}}=(I+F\Delta{t})\delta{x}δx=δx+δx˙=(I+FΔt)δx
当然,在上述的微分方程中,还有一些变量如a n , w n a_n,w_nan,wn,同时因为加速度和角速度的bias的误差量是不知道的,因此在这里要对这两个变量加入随机的噪声a w , b w a_w, b_waw,bw。这些变量都作为输入变量U,因此在状态更新的过程中,除了状态转移矩阵之外,还有驱动矩阵,有:
δ x = ( I + F Δ t ) δ x + F i U \delta{x}=(I+F\Delta{t})\delta{x}+F_iUδx=(I+FΔt)δx+FiU
有了状态转移矩阵和驱动矩阵,我们很容易就能得到状态的转移和协方差的更新方程,有
P = ( I + F Δ t ) P ( I + F Δ t ) T + F i Q F i T P=(I+F\Delta{t})P(I+F\Delta{t})^T+F_iQF_i^TP=(I+FΔt)P(I+FΔt)T+FiQFiT
总结
上面就是对ESKF的一个简单总结,下面说一下这个理论的实际用处,笔者是在看VINS的过程中,接触到的这个理论,其中VINS把上面得到的状态转移矩阵用在了两个地方,1). 优化过程中,当得到新的bias之后,使用一阶泰勒展开的形式更新所有的预积分结果;2). 优化过程中,作为求解bias增量时的jacobian。
开始的时候,笔者一直没有搞懂为什么上面的过程得到的状态转移矩阵可以用在这些地方,毕竟我们知道,上面的两个地方本质上都是泰勒的阶展开,而一阶展开明确的公式就是f ( x + δ x ) = f ( x ) + J δ x f(x+\delta{x})=f(x)+J\delta{x}f(x+δx)=f(x)+Jδx,而上面的状态转移矩阵中的各个项是否能够代替上面的jacobian呢?答案是肯定的!
比如我们对速度V求与加速度bias的导数,那么根据求导的定义
d V d a b = lim δ a b → 0 V ( a b + δ a b ) − V ( a b ) δ a b \frac{dV}{da_b}=\lim_{\delta{a_b}\rightarrow0}\frac{V(a_b+\delta{a_b})-V(a_b)}{\delta{a_b}}dabdV=δab→0limδabV(ab+δab)−V(ab)
发现了么?如果我们把分子中的V ( a b + δ a b ) V(a_b+\delta{a_b})V(ab+δab)看做V t V_tVt,同时再对所有的V对时间求导,就得到:
d V ˙ d a b = lim δ a b → 0 V t ˙ − V ˙ δ a b \frac{d\dot{V}}{da_b}=\lim_{\delta{a_b}\rightarrow0}\frac{\dot{V_t}-\dot{V}}{\delta{a_b}}dabdV˙=δab→0limδabVt˙−V˙
其实就对应于状态转移矩阵中的对应项了。其他的也是同理,这里就不再赘述了。