??个人主页:研学社的博客
????欢迎来到本博客❤️❤️??
?博主优势:???博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
???本文目录如下:???
目录
?1 概述
现代医学需要复杂的信号表示方法来应对不断增长的数据量。这些方法的重要标准主要是低计算和存储成本,而基础数学模型仍然应该对数据分析师具有可解释性和意义。满足这些标准的最有希望的模型之一是基于Hermite函数,但是对于特定的生物医学波形有一些重要的限制。我们通过使用加权Hermite函数扩展了该模型,并开发了一种基于梯度的约束优化方法,以使系统适应不同类型的信号。为了证明我们方法的潜力,我们考虑了心电图信号压缩的问题。MIT / BIH心律失常数据库的实验显示,与使用经典Hermite函数的前工作相比,有显着改善。
?2 运行结果
2.1 算例1
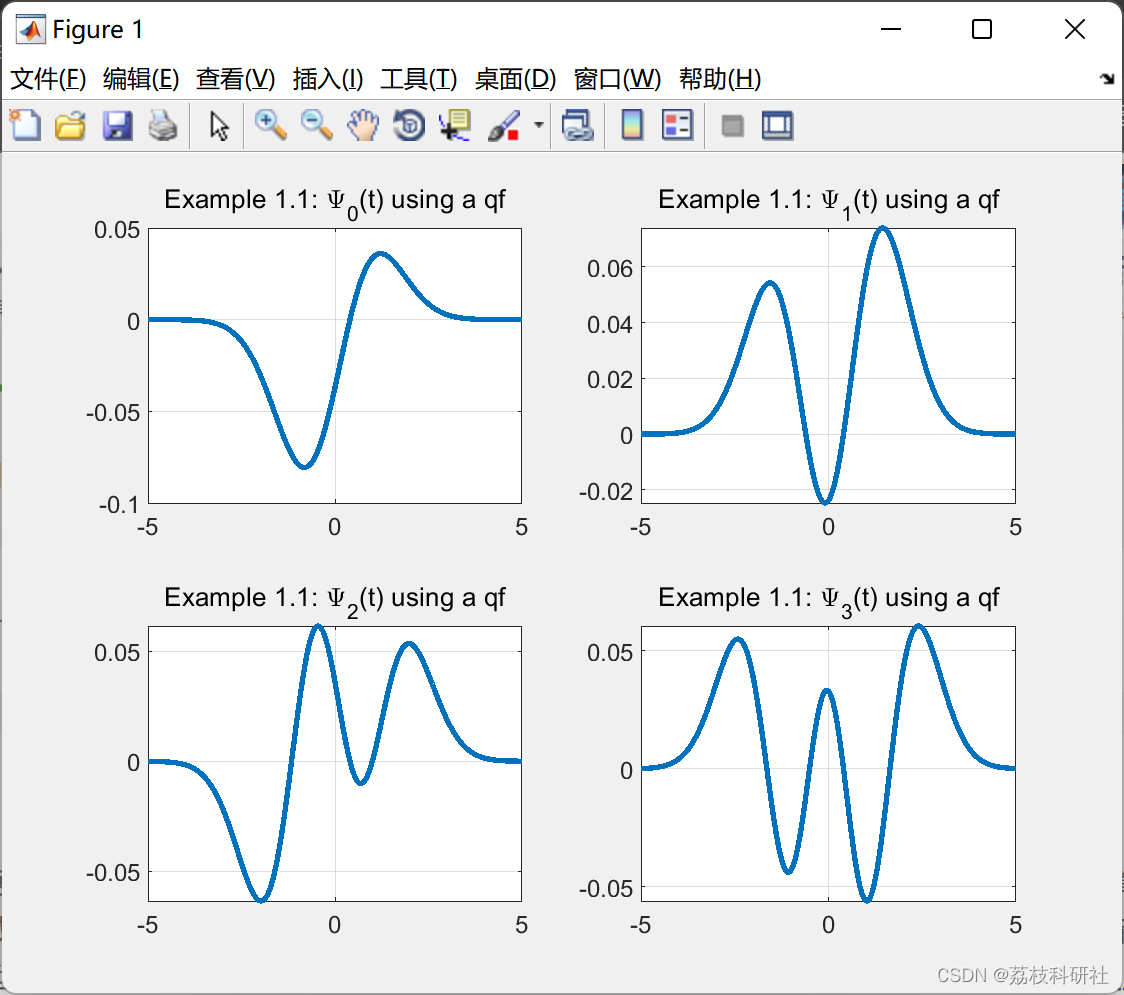
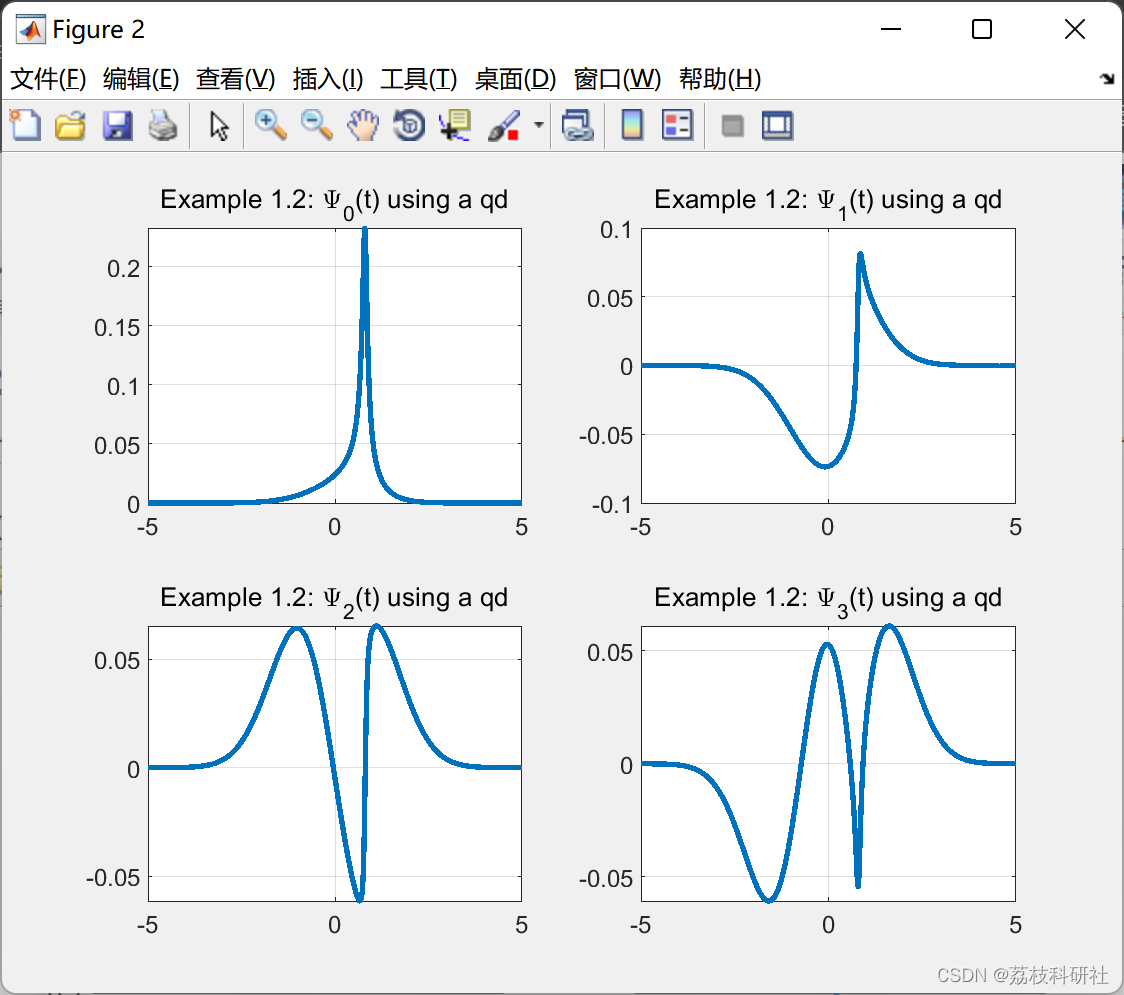
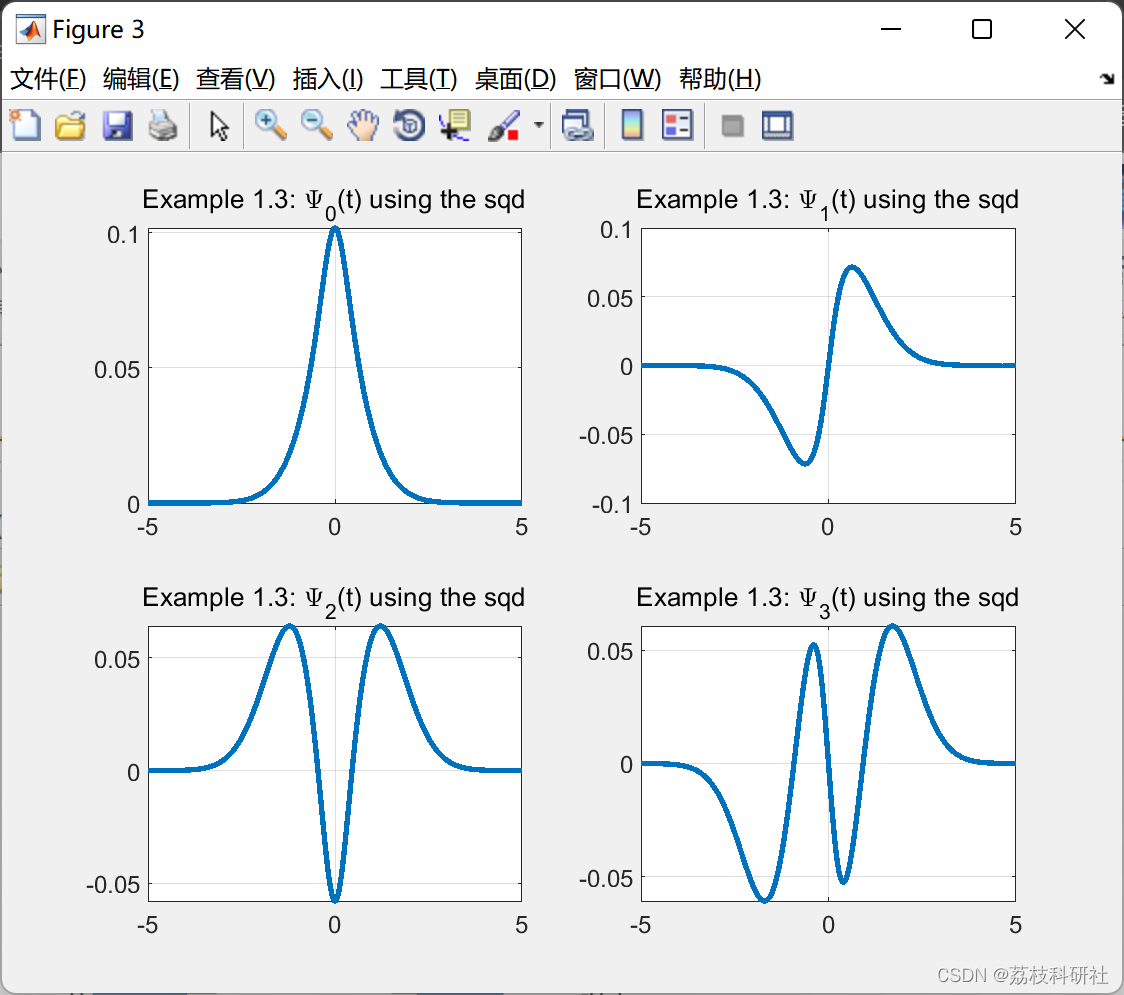
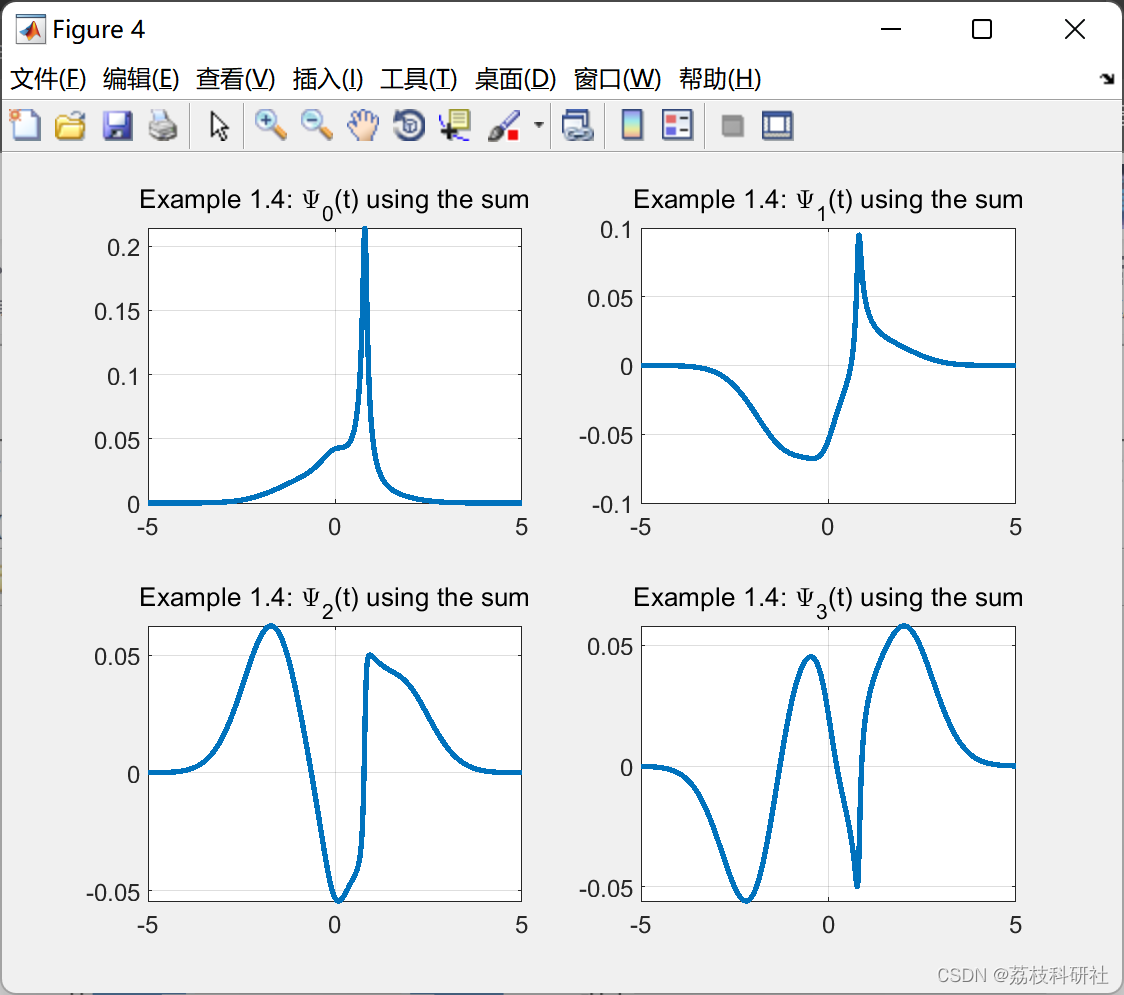
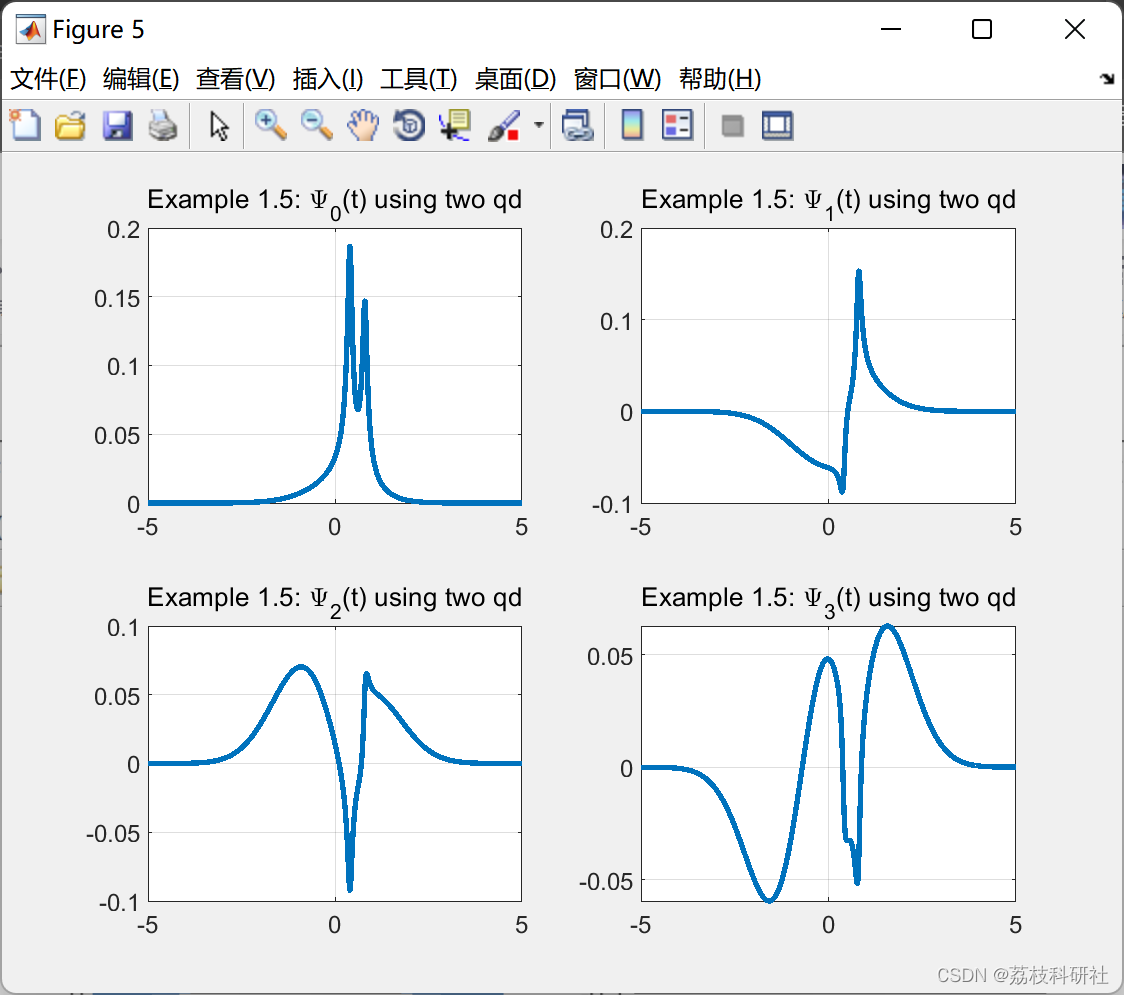
2.2 算例2
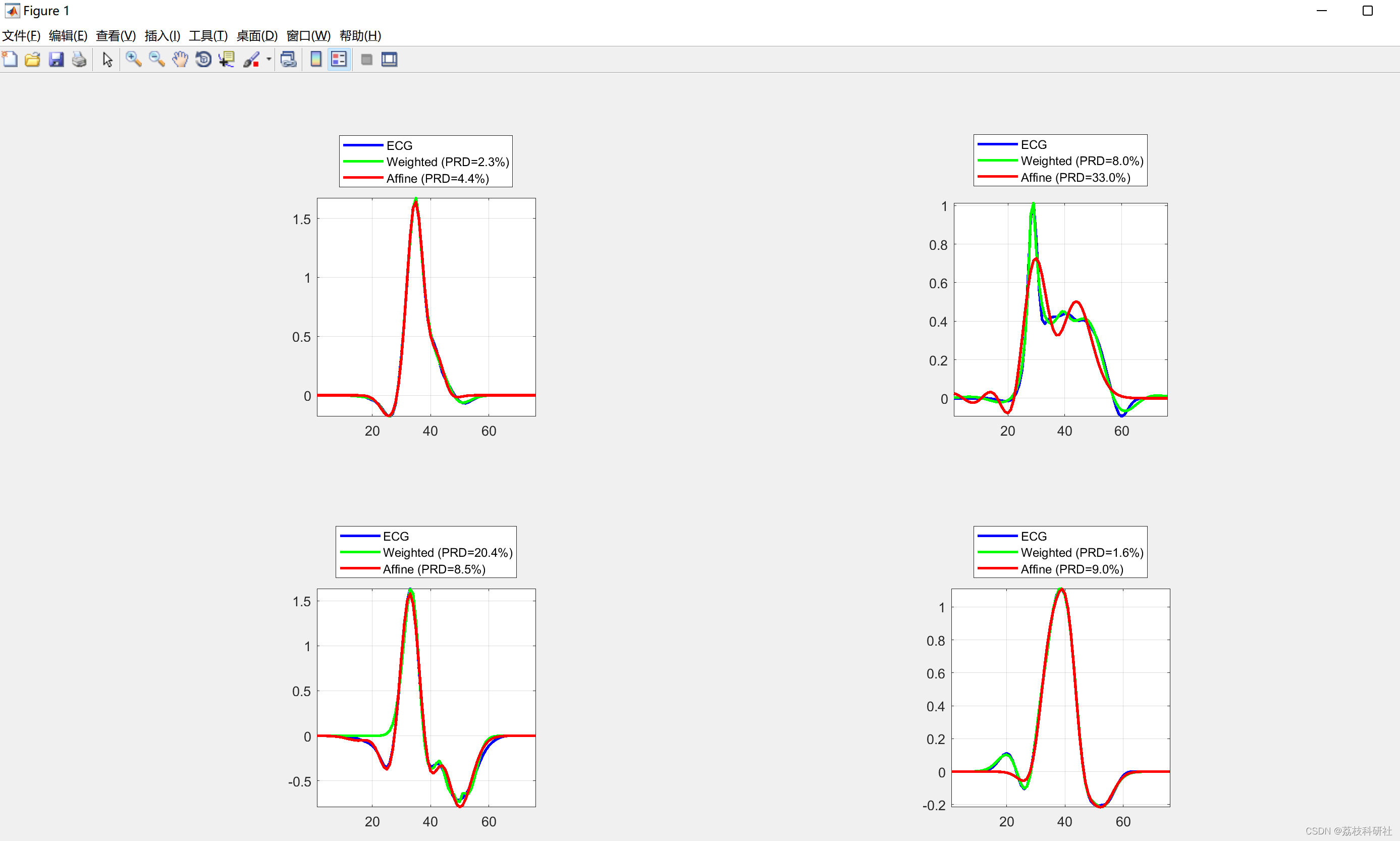
2.3 算例3
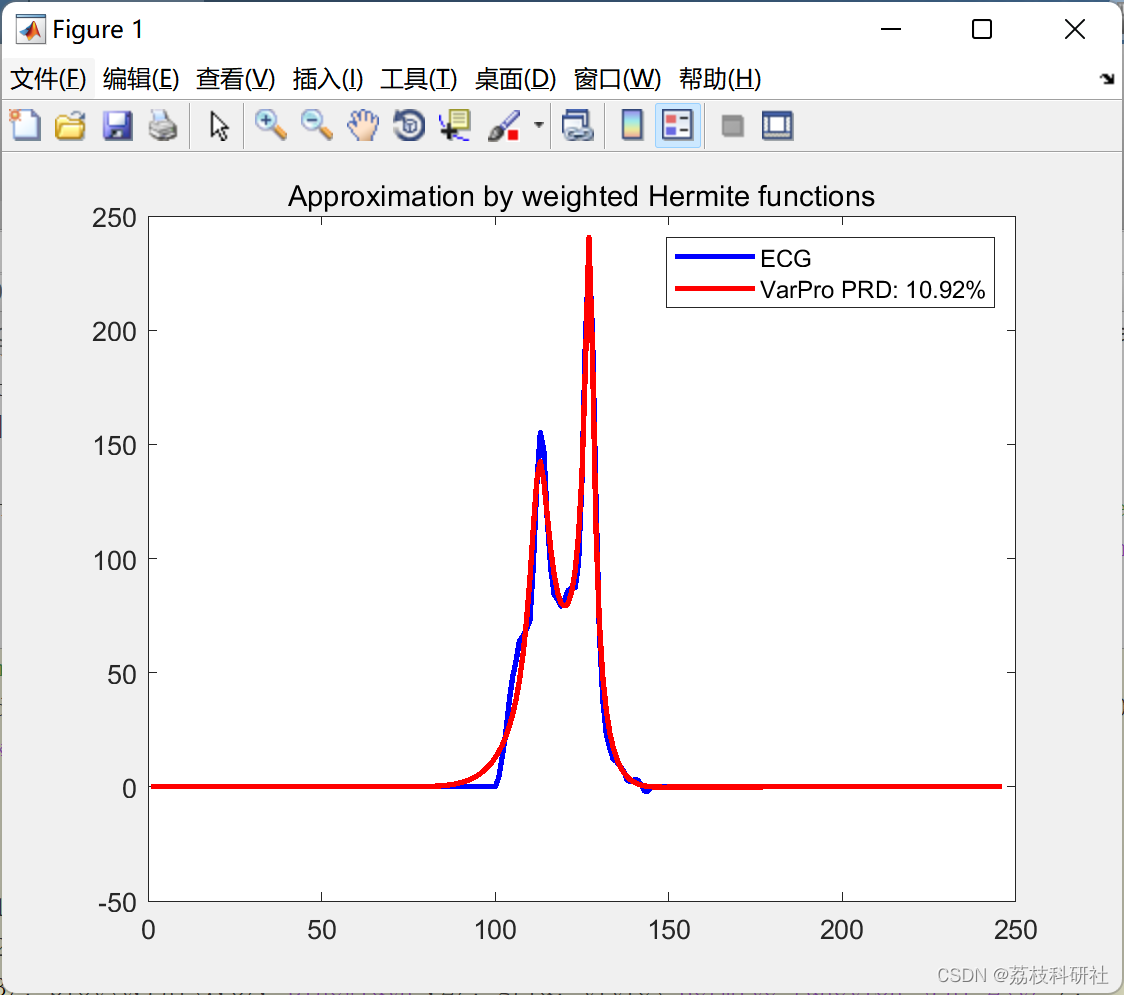
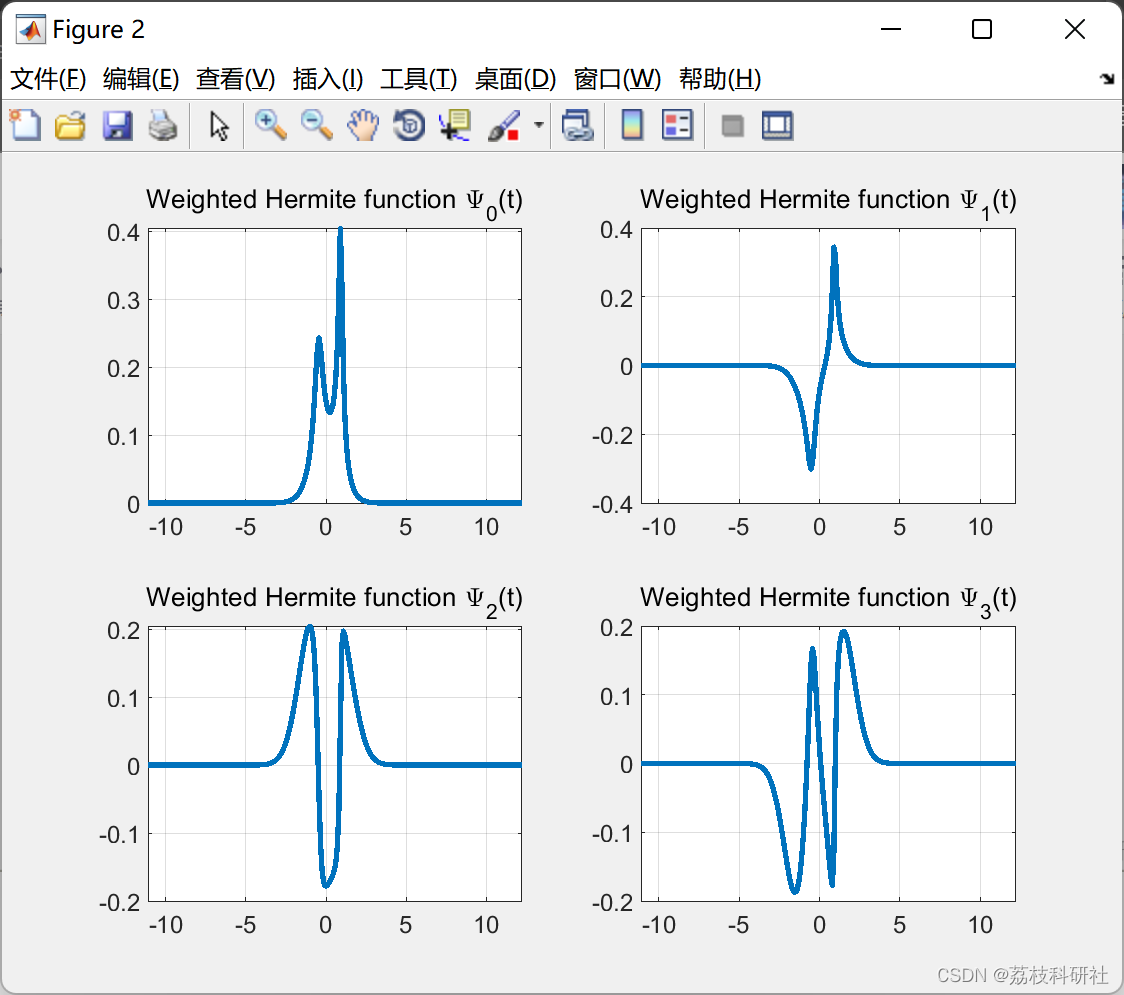
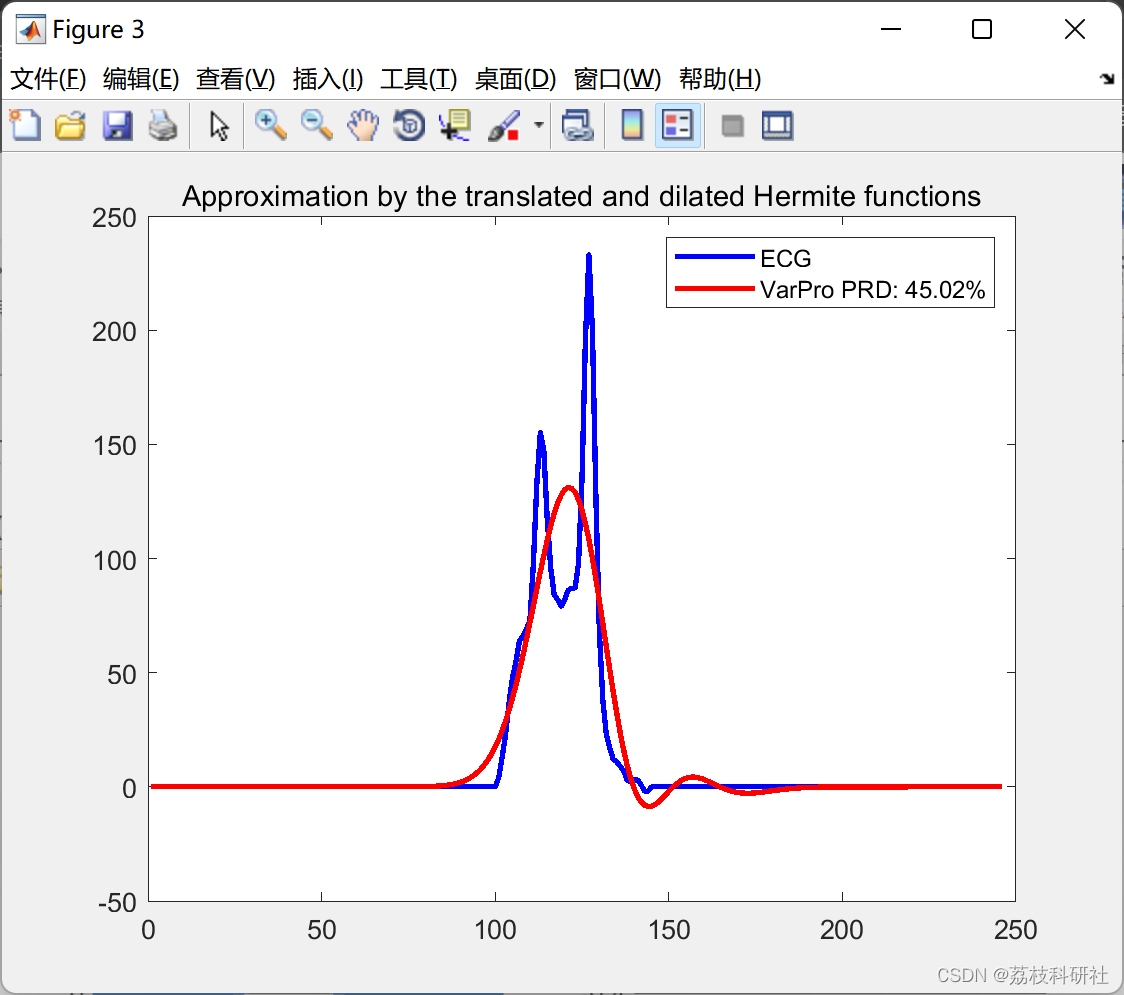

2.4 算例4
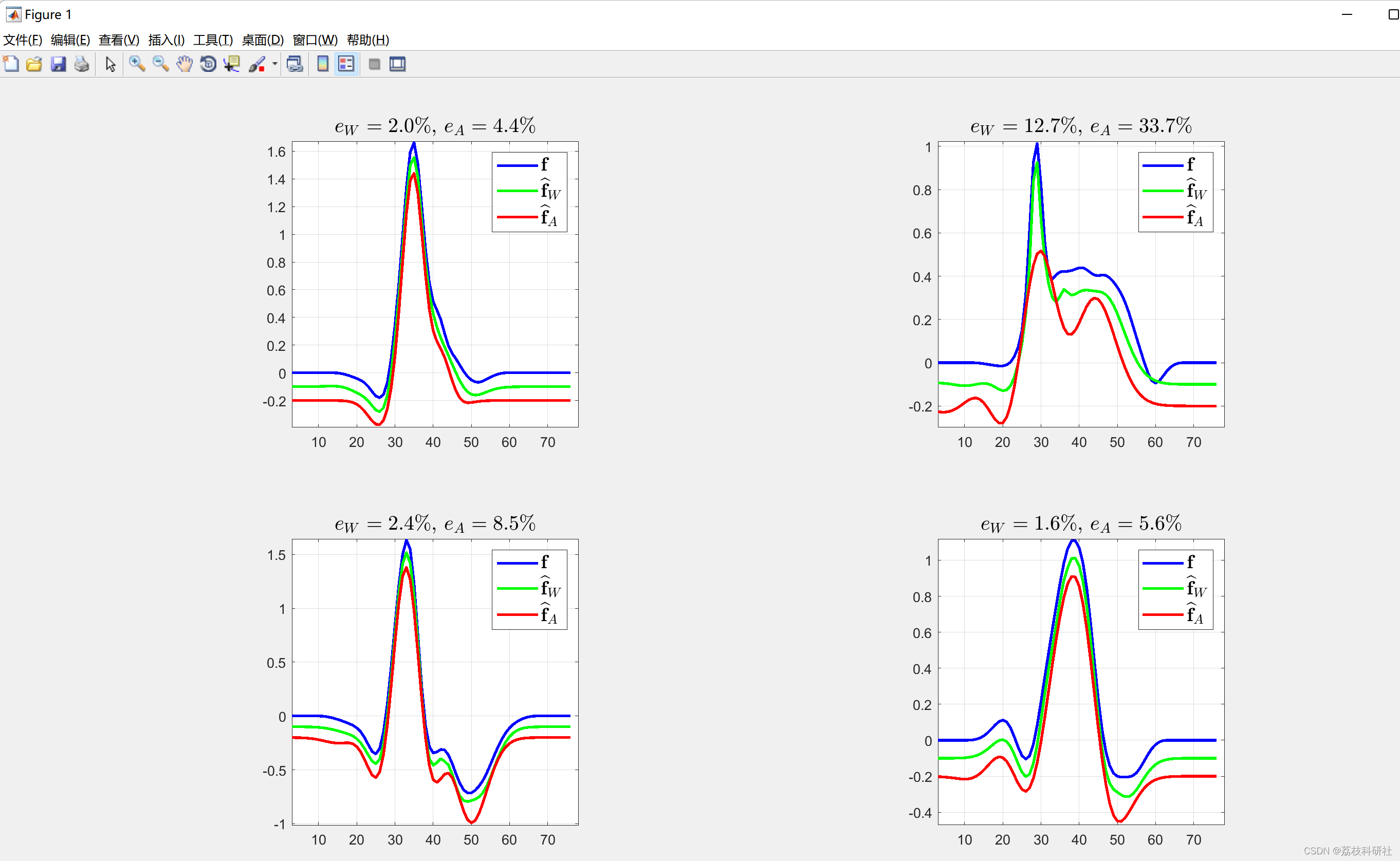
2.5 算例5
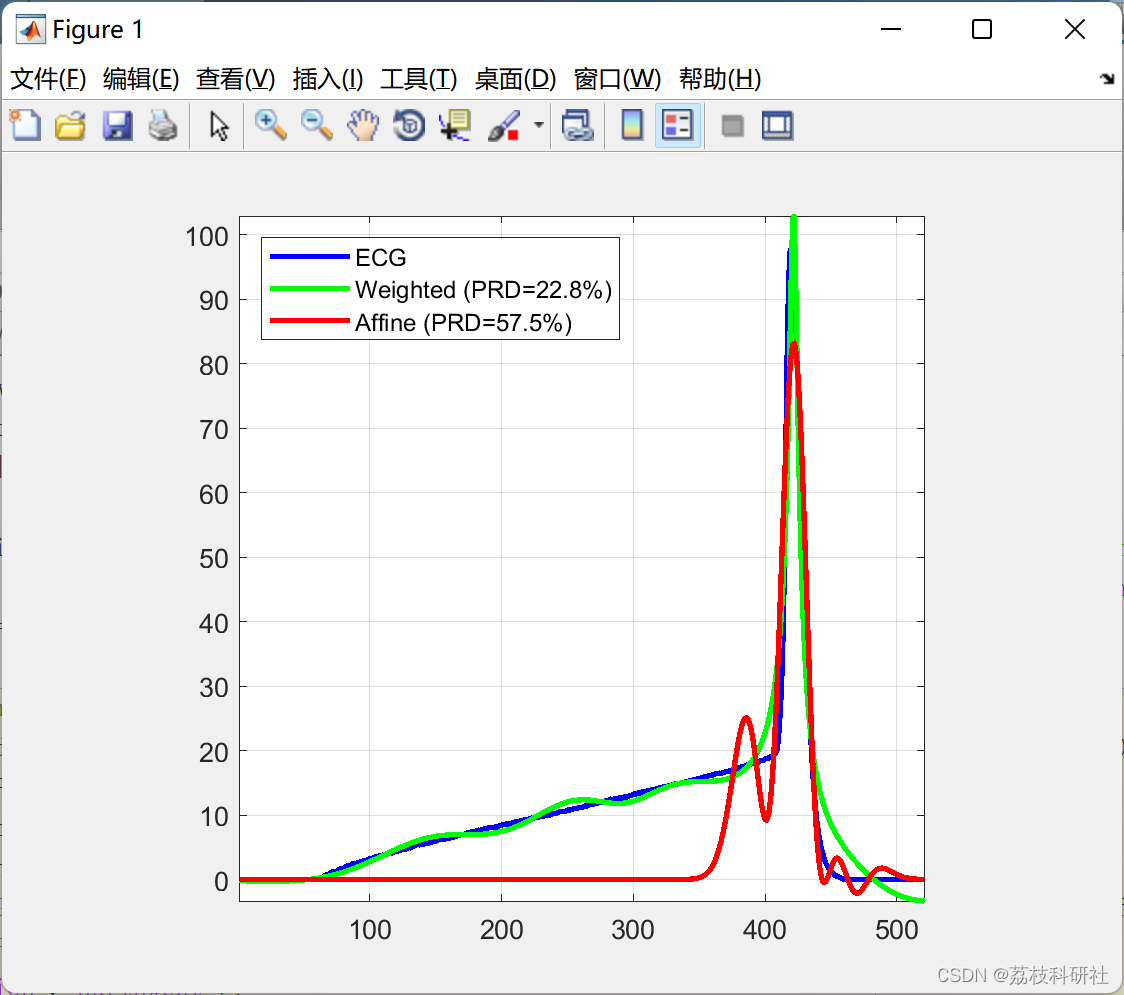
2.6 算例6
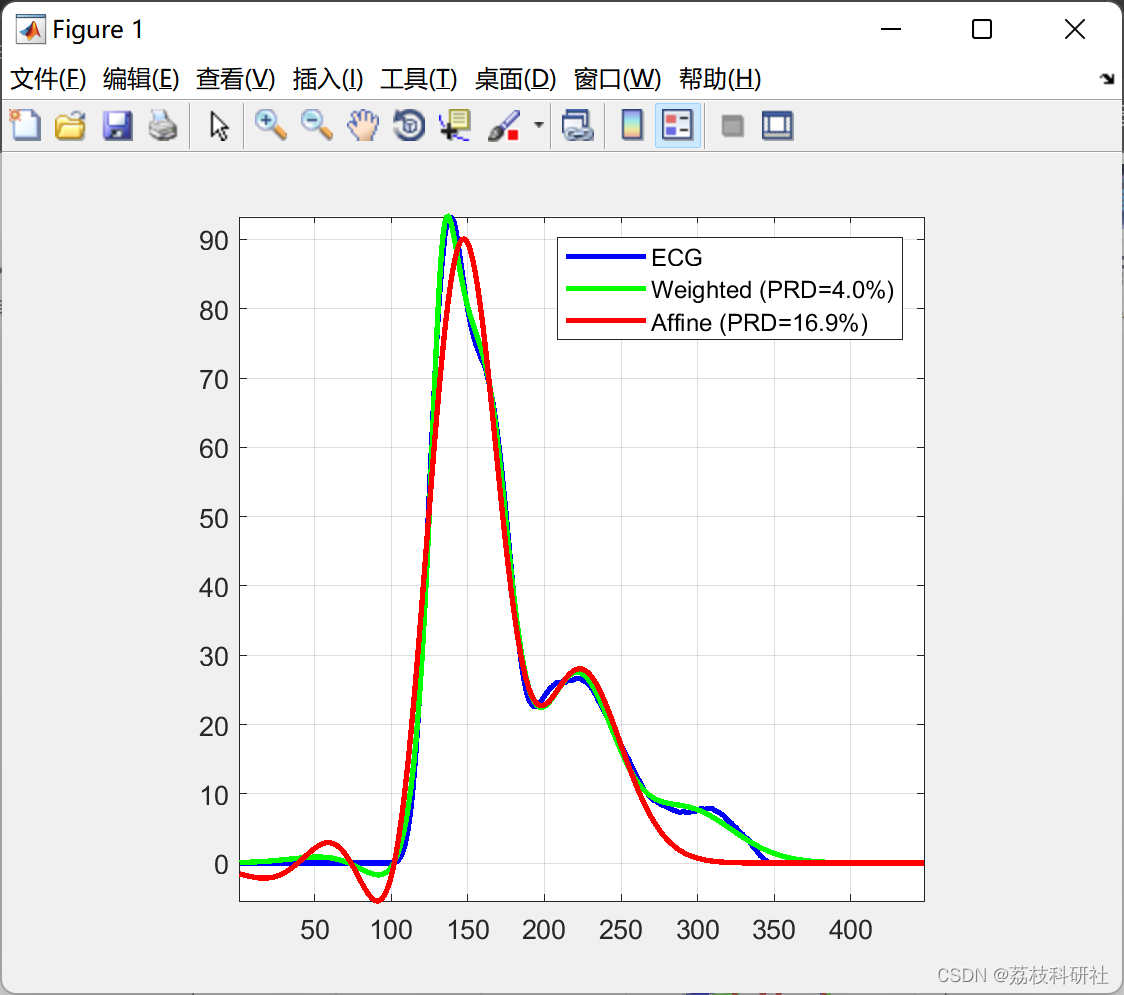
部分代码:
%% Computing the modified weight function of the Hermite system.
%
% Usage:
% [WF, dWF, Ind, t] = weight_function(signal,systems,eta)
%
% Input parameters:
% N : the weight function will be evaluated at 'N' number of points.
% systems : cell array that describes the structure of the modified weight function.
% systems{i}{1} is the name of the ith factor (qf, qd, sqd, hms).
% systems{i}{2} is the number of basis function 'n' (it should be the same for all factors).
% systems{i}{3} contains the positions of the corresponding free parameters of the ith factor in 'eta'.
% In the example below, systems{1}{3}=1, thus the 'x' parameter of the quadratic factor is equal to eta(1).
% systems{i}{4:5} lower and upper bounds for the free parameters of the ith factor.
% systems{i}{6} precomputed recurrence coefficients (eta_k, beta_k) of the orthogonal polynomials.
% If there are no precomputed recurrence coefficients, set this parameter to [].
%
% eta : vector of free parameters including the parameters of
% the weight function, the translation and the dilation.
%
% Output parameters:
% WF : it is the modified weight function corresponding to 'systems' and 'eta'.
% dWF : contains the partial derivatives of WF with respect to the free parameters in eta.
% Ind : Column l of dWF contains the partial derivative of WF with respect to eta(i),
% where 1 = Ind(1,l) and i = Ind(2,l). Those partial derivatives that are independent of
% eta(i) are equal to zero and so they are not stored in dWF. That is why the index array 'Ind' is required.
% t : the weight function and its derivatives are evaluated at the points of 't'.
function [WF, dWF, Ind, t] = weight_function(N,systems,eta)
% Extracting the dilation and translation parameters.
for i=1:length(systems)
if strcmp('hms',systems{i}{1})
dilatind=systems{i}{3}(1);
transind=systems{i}{3}(2);
dilation=eta(dilatind);
translation=eta(transind);
end
end
n=length(systems);
trans=round(N/2)-translation; %Distance from the mid point.
if ~mod(N,2)
t=(-N/2:N/2-1)';
else
t=(-floor(N/2):floor(N/2))';
end
t=dilation*(t+trans);
t=reshape(t,N,1);
% Computing the weight function and its derivatives.
eta=reshape(eta,length(eta),1);
v1=zeros(N,n); v2=zeros(N,n); v3=zeros(N,n);
dtv1=zeros(N,n); dtv2=zeros(N,n); dtv3=zeros(N,n);
dxv1=zeros(N,n); dyv2=zeros(N,n); dzv2=zeros(N,n); dsv3=zeros(N,n);
only_qf=false;
Ind=ones(2,length(eta));
x=zeros(1,n); y=zeros(1,n); z=zeros(1,n); s=zeros(1,n);
xind=zeros(1,n); yind=zeros(1,n); zind=zeros(1,n); sind=zeros(1,n);
top=[0 0 0];
for i=1:n
switch systems{i}{1}
case 'qf' %quadratic factor v1(t)=(t-x)^2
xind(top(1)+1)=systems{i}{3};
x(top(1)+1)=eta(xind(top(1)+1));
v1(:,top(1)+1)=(t-x(top(1)+1)).^2;
dtv1(:,top(1)+1)=2*(t-x(top(1)+1));
dxv1(:,top(1)+1)=-2*(t-x(top(1)+1));
top(1)=top(1)+1;
if 2==n
sqrtv1=t-x(top(1)+1);
only_qf=true;
end
case 'qd' %quadratic divisor v2(t)=1/((t-y)^2+z^2))
yind(top(2)+1)=systems{i}{3}(1);
zind(top(2)+1)=systems{i}{3}(2);
y(top(2)+1)=eta(yind(top(2)+1));
z(top(2)+1)=eta(zind(top(2)+1));
v2(:,top(2)+1)=1./((t-y(top(2)+1)).^2+z(top(2)+1).^2);
dtv2(:,top(2)+1)=-2.*(t-y(top(2)+1))./((t-y(top(2)+1)).^2+z(top(2)+1).^2).^2;
dyv2(:,top(2)+1)=2*(t-y(top(2)+1))./((t-y(top(2)+1)).^2+z(top(2)+1).^2).^2;
dzv2(:,top(2)+1)=-2.*z(top(2)+1)./((t-y(top(2)+1)).^2+z(top(2)+1).^2).^2;
top(2)=top(2)+1;
only_qf=false;
case 'sqd' %symmetric quadratic divisor v3(t)=1/(t^2+s^2)
sind(top(3)+1)=systems{i}{3};
s(top(3)+1)=eta(sind(top(3)+1));
v3(:,top(3)+1)=1./((t.^2+s(top(3)+1)^2));
dtv3(:,top(3)+1)=-2*t./((t.^2+s(top(3)+1)^2)).^2;
dsv3(:,top(3)+1)=-2*s(top(3)+1)./((t.^2+s(top(3)+1)^2)).^2;
top(3)=top(3)+1;
only_qf=false;
case 'hms' %classical Hermite weight function w(t)
w=exp(-t.^2); %classical Hermite weight function
dtw=-2*t.*exp(-t.^2); %first derivative of the classical Hermite weight function
sqrtw=exp(-t.^2/2); %square root of w
otherwise
error('Invalid system parametrization.');
end
end
xind(top(1)+1:end)=[]; yind(top(2)+1:end)=[]; zind(top(2)+1:end)=[]; sind(top(3)+1:end)=[];
x(top(1)+1:end)=[]; y(top(2)+1:end)=[]; z(top(2)+1:end)=[]; s(top(3)+1:end)=[];
v1=sum(v1,2); dtv1=sum(dtv1,2); dxv1(:,top(1)+1:end)=[];
v2plot=v2(:,1:top(2));
v2=sum(v2,2); dtv2=sum(dtv2,2); dyv2(:,top(2)+1:end)=[]; dzv2(:,top(2)+1:end)=[];
v3=sum(v3,2); dtv3=sum(dtv3,2); dsv3(:,top(3)+1:end)=[];
if only_qf
sqrtv=sqrtv1.*sqrtw; %Special case when the square root of the modified weight function can be calculated explicitly.
sqrtdtv=sqrtw - sqrtv1.*t.*sqrtw;
sqrtdxv=-sqrtw;
WF=sqrtv;
dWF=[sqrtdtv.*t./dilation, -sqrtdtv.*dilation, sqrtdxv];
Ind=[1 1 1;dilatind,transind,xind];
elseif 1==length(systems) %No weighted modification, the classical Hermite functions are used.
WF=sqrtw;
sqrtdtv=-sqrtw.*t;
dWF=[sqrtdtv.*t./dilation, -sqrtdtv.*dilation];
Ind=[1 1;dilatind,transind];
else
% This is a stable formula for calculating the derivatives,
% by cancelling out w from the denominator.
sqrtsumv123=sqrt(v1+v2+v3);
sqrtv=sqrtsumv123.*sqrtw;
sqrtdtv=0.5./sqrtsumv123 .* ((dtv1+dtv2+dtv3).*sqrtw - (v1+v2+v3).*2.*t.*sqrtw);
sqrtdxv=0.5./sqrtsumv123.*sqrtw.*dxv1;
sqrtdyv=0.5./sqrtsumv123.*sqrtw.*dyv2;
sqrtdzv=0.5./sqrtsumv123.*sqrtw.*dzv2;
sqrtdsv=0.5./sqrtsumv123.*sqrtw.*dsv3;
WF=sqrtv;
dWF=[sqrtdtv.*t./dilation, -sqrtdtv.*dilation, sqrtdxv, sqrtdyv, sqrtdzv, sqrtdsv];
Ind=[ones(1,length(eta)); dilatind,transind,xind,yind,zind,sind];
%Remove constant zero partial derivatives.
dWF(:,0==Ind(2,:))=[];
Ind(:,0==Ind(2,:))=[];
end
end
?3 Matlab代码实现
?4 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]Péter Kovács, Carl Böck, Tamás Dózsa, Jens Meier, Mario Huemer (2018) Waveform modeling by adaptive weighted Hermite functions
