一、涉及的概念
随机:随机是指信号的取值服从某种概率规律,这一规律可以是完全已知的、部分已知的或完全未知的。随机信号也称为随机过程、随机函数或随机序列。
确定性信号:如果序列{s(t)}在每个时刻的取值不是随机的,而是服从某种固定函数的关系,则称之为确定性信号。如阶跃信号、符号信号或矩形脉冲等。
随机信号:若序列{s(t)}在每个时刻的取值是随机变量,则称之为随机信号。随机信号过过程可以用概率分布特性(简称统计性能)统计地描述。
令x(t)表示一连续时间的复随机过程,对于任何一固定的时刻t,随机过程x(t)定义一随机变量X=x(t).令u(t)表示其均值,则:
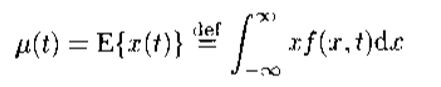
式中f(x,t)表示随机变量X = x(t) 在时间t的概率密度函数。
自相关函数Rx(t1,t2)定义为x(t)在时刻t1和t2之间的相关,即:
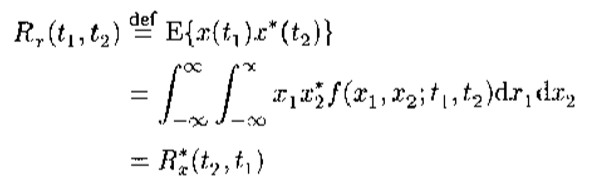
式中,上标*表示复数的共轭;f(x1,x2;t1,t2)表示随机变量X1 = x(t1)和X2 = x(t2)的联合概率密度函数。一般情况下,自相关函数与时间变量t1和t2有关。
均值和自相关函数分别是随机信号x(t)的一阶矩和二阶矩,类似地还可以定义随机信号的K阶矩:
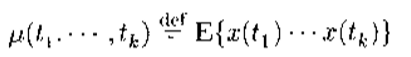
根据K阶矩是否与时间有关,随机信号又分为平稳随机信号和非平稳随机信号两大类。
平稳信号:n阶平稳、广义平稳、严格平稳。平稳信号常称为时不变信号,即统计量不随时间变化的信号。
非平稳信号:也常称为时变信号,因为它至少有某个统计量(如均值,协方差函数)是时间的函数。
注意:时变与时不变信号不应该理解为信号的取值或波形是否随时间变化。
遍历性:它关心的问题是从随机信号的依次记录是否可以估计其统计量(如相关函数,功率谱等)。常用一种遍历性形式,均方遍历性。
当一个信号是n阶矩均方遍历的平稳过程时,它的n阶及所有低阶的统计平均都可以用各自的时间平均来代替。换句话说,这些统计量均可以根据该信号的一次观测数据进行估计。如果均方遍历的平稳信号x(t)的N个观测样本x(1),x(2),...,x(N),为已知,则信号的均值ux可由时间平均估计。
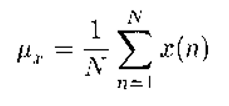
统计特性:一阶、二阶、高阶(三阶及以上)
二、相关函数、协方差函数与功率谱密度
相关函数、协方差函数与功率谱密度是描述平稳随机信号统计特性最常用的二阶统计量。
2.1 单个随机信号x(t)——自相关函数、自协方差函数与功率谱密度
自相关函数、自协方差函数
令x(t)是一取复值的广义平稳随机信号,时间变量t属于负无穷—正无穷或者零—正无穷。意味着随机信号x(t)的均值与时间t无关,为常数。令
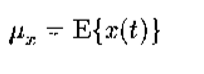
则x(t)在t1和t2的自相关函数和自协方差函数仅决定于时间差t1-t2,分别定义为;
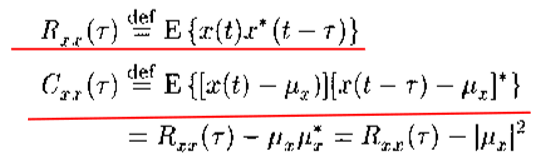
自相关函数和自协方差函数常称为相关函数和协方差函数,它们的变元τ表示两个信号取值的时间差,称为滞后。
(1)对于具有零均值的随机信号x(t)而言,自协方差函数与自相关函数等价;
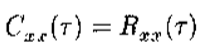
(2)当τ=0时,信号x(t)的自相关函数退化为x(t)的二阶矩,即
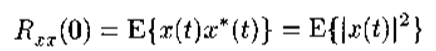
(3)当τ = 0时,信号x(t)的自协方差函数退化为x(t)的方差,即
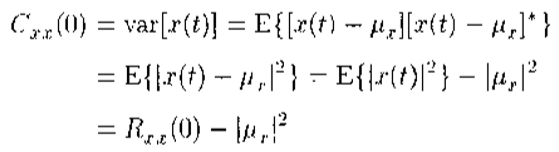
功率谱密度:
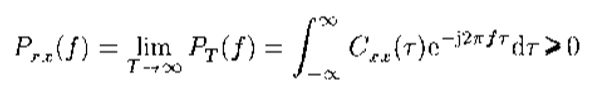
性质:
(1)功率谱密度是实的;
(2)功率谱密度是非负的,即大于等于零;
(3)自协方差函数是功率谱密度的傅里叶反变换,即;
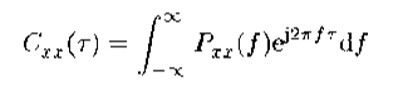
(4)若x(t)是零均值的随机过程,则协方差函数与相关函数等价,此时;
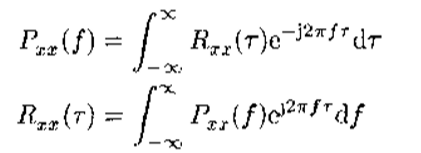 实际上,这个关系就是维纳辛钦定理。
实际上,这个关系就是维纳辛钦定理。
文字表述为:任意一个零均值的广义平稳随机过程的功率谱和它的自相关函数组成一个傅里叶变换对。
若功率谱等于常数,则随机过程称为白噪声;之所以称为白噪声是因为它的功率(或能量)与频率无关,具有与白色光相同的能量分布性质。相反,功率谱不等于常数的噪声称为有色噪声。
自相关函数矩阵:

这种矩阵叫做Toeplitz矩阵,对角线元素相同,而且其他对角线也分别具有相同的元素。 由于Rxx(-K)= Rxx*(K),故一个N*N阶的Toeplitz矩阵由它的N个自相关函数Rxx(0),Rxx(1),...Rxx(N-1)所决定。
半正定矩阵:所有特征值是正的或零值,不能为负值。半正定性是相关函数矩阵具有的一个重要性质。
2.2 两个随机信号x(t)和y(t)——互相关函数、互协方差函数与功率谱密度
互相关函数、互协方差函数:
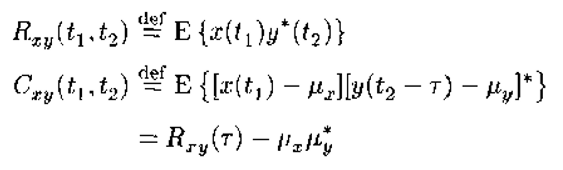
互相关系数:

互相关系数物理解释:
互协方差函数涉及两个不同信号x(t)和y(t)之间的相乘,一般来说,这两个减去均值的信号存在共性部分(确定量)和非共性部分(随机量),而共性部分的相乘总是去相同的符号,使得该部分得到加强而保留下来。与之不同,两个信号的非共性部分是随机的,它们的乘积有时取负,有时取正,通过数学期望的平均运算后,趋于相互“抵消”。
这意味着,互协方差函数能够把两个信号之间共性部分提取出来,并抑制掉非共性部分。因此,互协方差函数描述了两个信号之间的相关(联)程度。但是这种相关程度是用绝对量来衡量的,并不方便。对互协方差函数做归一化处理,得到互相关系数后,两个信号之间的相关程度就很容易度量了。
若互相关系数越接近于1,则两个信号越相似;反之,互相关系数越接近于0,两个信号的差异就越大。
互功率谱密度:定义为互协方差函数的傅里叶变换;
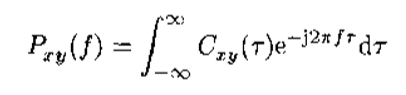
互功率谱密度的实部称为同相谱,虚部称为正交谱,记为
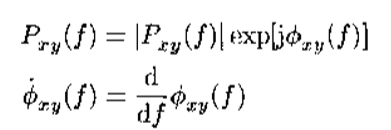

相干函数:

2.3 小结
相关函数、协方差函数及相关系数等描述信号在时间域(主要是滞后)的统计特性,属于时域特性;而功率谱密度和相干函数等则描述信号在频率域的统计性质,归为频域特性。由于协方差函数和功率谱密度可以通过傅里叶变换相互转换,所以信号的时域特性和频域特性具有同等重要的作用。
概率密度分布服从正态分布的随机信号称为高斯随机信号,而具有非正态分布的随机信号称为非高斯随机信号。对于非高斯信号,仅使用相关函数和功率谱是不能完全描述信号的统计性质的,这是需要用到三阶甚至更高阶的统计量,它们统称为高阶统计量。包含高阶矩,高阶累积量,高阶谱等。
在进行平稳信号的处理之前,通常需要先估计信号的均值,然后对每个信号值减去该均值。这一处理称为平稳信号的零均值化。由于零均值化是信号处理的必然预处理,所以在很多文献中将相关函数和协方差函数混用,因为零均值信号的相关函数和协方差函数二者是等价的。
三、两个信号的比较与识别
3.1 独立、不相关、正交


![]()

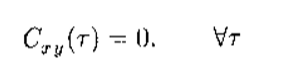

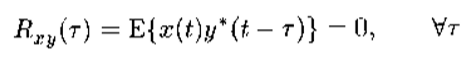
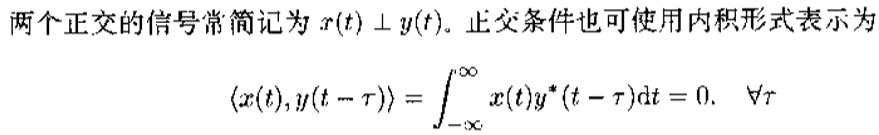
![]()

![]()
![]()


![]()

![]()
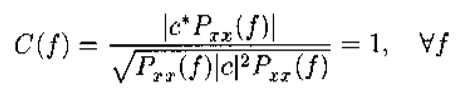

3.2 信号变换
同时适用于均匀和非均匀采样信号的工具。
如:傅里叶变换、K-L变换
(1)将一个信号展开为级数形式, φk有何种要求?Ck如何确定?展开系数Ck是使用信号x(t)某种积分形式来确定的,这一积分分式习惯称为信号变换。
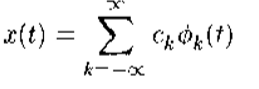
(2)如傅里叶变换
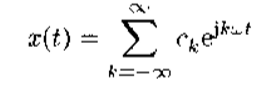
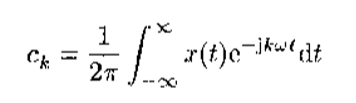 这个就是信号变换公式
这个就是信号变换公式
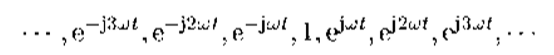 称为傅里叶展开的基函数
称为傅里叶展开的基函数
(3)使用正交基函数的信号变换称为正交信号变换;使用非正交基函数的信号变换称为非正交信号变换;
3.3 多项式序列的斯密特标准正交化
四、具有随机输入的线性系统
(1)系统输出的功率谱密度
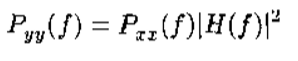

![]()
(2)窄带功率谱估计



申明:内容依据张贤达教授所著《现代信号处理》第二版所总结归纳