01背包问题
01背包问题(0-1 Knapsack):是指给你一个有限容量的背包,然后在给你一堆价值、体积不同的物品,使用这个背包去装物品,每件物品只能使用一次,问这个背包能够装入物品的最大价值是多少?
PS:当然这只是01背包问题最常见的一种形式,它还有很多种变式
?题目
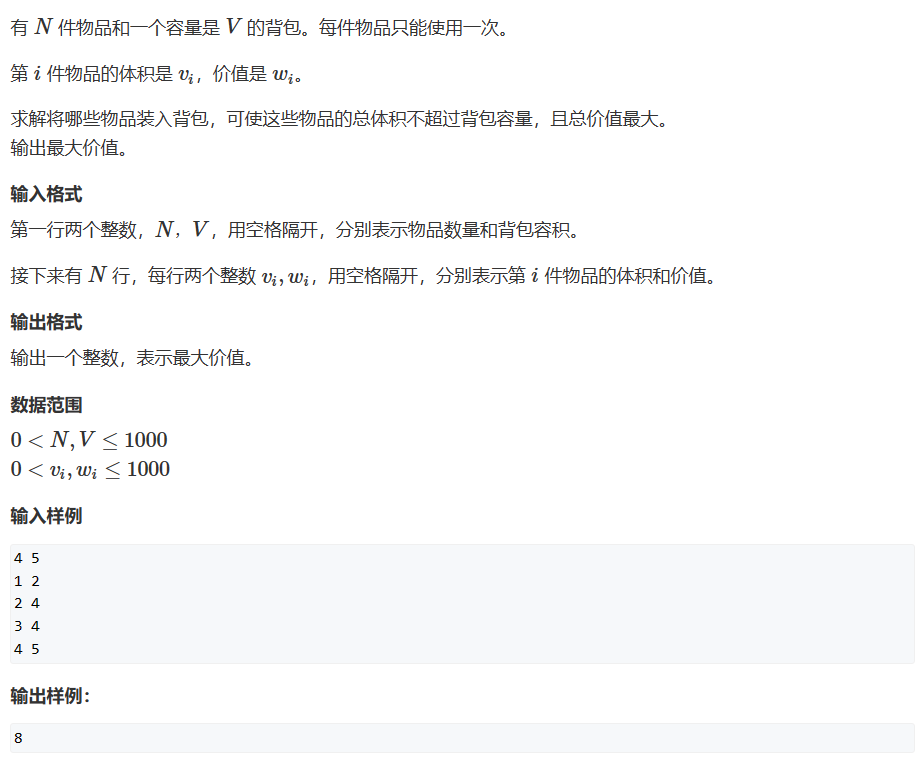
题目来源:2. 01背包问题 - AcWing题库
?分析
大致思路:01背包问题是一个很经典的动态规划的题目,而动态规划题目的核心就是求解状态转移方程1,通过状态转移方程我们可以得到状态数组2,最终根据这个状态数组得到我们需要的结果
PS:动态规划的题目基本上都是上面这个思路,难就难在状态转移方程的求解?
朴树版详细思路:(主要是推导状态转移方程是如何得来的)
Step1:接受输入。需要准备状态数组,用于存储所有的状态
Step2:求解状态转移方程。可以根据当前放入物品(设当前放入背包的是第
i个物品)的体积得到两种情况情况一背包的最大容量不能装下第
i个物品,最大价值就是装入第i-1个物品时的最大价值。代码为:f[i][j] = f[i - 1][j],意思是当背包最大体积为j时,最大价值物品的集合是从第1~(i-1)个物品中选出的情况二背包的最大容量能装下第
i个物品,此时又出现了两种情况,因为背包的最大容量能装入第i个物品,并不能代表背包当前剩余的容量能够装入第i个物品一是背包不装第
i个物品,此时说明背包的剩余的容量肯定不能装入第i个物品。代码为:f[i - 1][j],意思是当前背包最大价值就是装入上一个(第i-1个)物品时的最大价值二是背包装入第
i个物品,此时说明背包肯定转入了第i个物品,但是不能确定是通过将前面放入背包的物品拿出来后才放入第i个物品的(背包剩余容量不足),还是直接将第i个物品放入(背包剩余容量充足)。代码为:f[i - 1][j - v[i]] + w[i],意思是当前背包最大体积为j时,最大价值物品的集合是从第1~i个物品中选出的,且最大价值物品的集合中一定含有第i个物品备注:
f[i - 1][j - v[i]] + w[i]的由来。我们无法直接获取装i的最优解,需要进行思维转换,因为按照意思,装i的代码应该是f[i][j],体积为 j 时,从第1~i个物品中选取最优解且必须选第i个物品,我们通过先将背包的容量减去第i个物品的体积,然后求得前i-1个物品的最优解,最后再加上第i个物品的价值,最终得到第i个物品的最优解(这一步是这一题最关键的一步,只要这里理解了,这题基本上就算解决了)
由于我们需要得到最大价值,所以需要取两种情况的最大值,即:
Math.max(f[i - 1][j], f[i - 1][j - v[i]] + w[i])
Step3:获取最大价值。通过状态转移方程对状态不断进行更新,同时将每次更新的状态存入状态数组中,最终可以得到所有的状态,而最终的状态就是01背包的答案
状态数组构建过程:
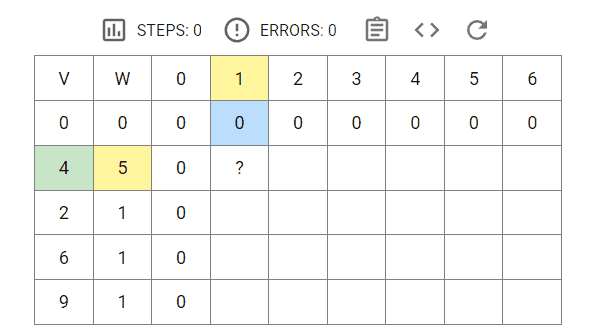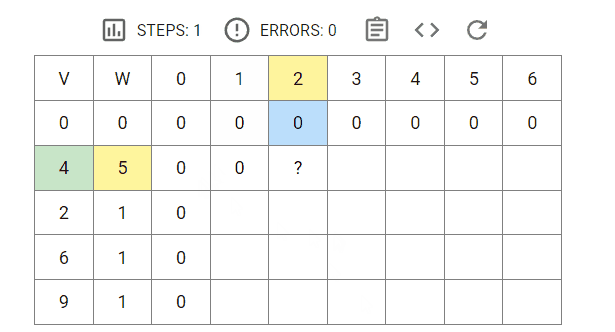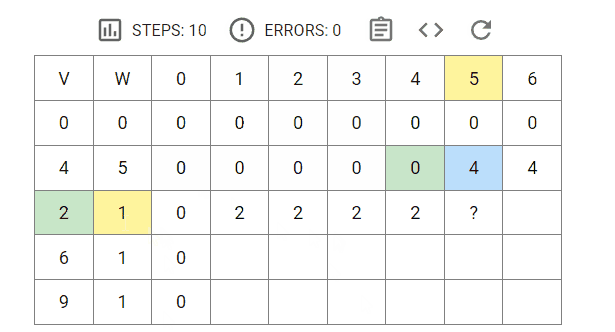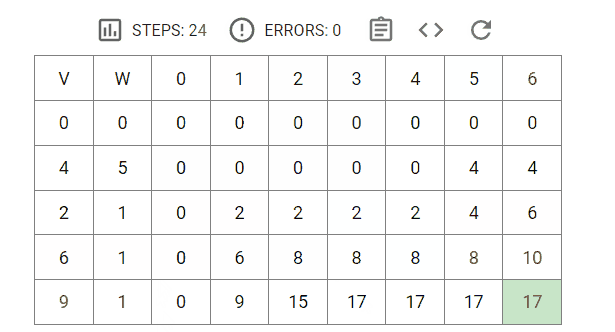
备注:V表示商品的价值,W表示商品的体积,背包最大容量为6
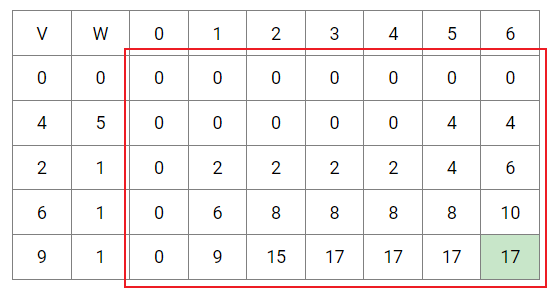
通过上面的状态数组(红框中的),我们可以得到背包装入物品的最大价值为17
精华版详细思路:(主要是推导状态转移方程是如何得来的)
- Step1:接受输入。需要准备状态数组,用于存储所有的状态
- Step2:求解状态转移方程。每次装入一件物品(设当前装入的是第
i件物品)都会出现一个最大值,而装入的状态无非两种,最大值的获取需要装入第i个物品,最大值的获取不需要装入第i个物品。- 情况1:背包体积不能装下第
i个物品。则 - 情况2:背包体积能装下第
i个物品。
- 情况1:背包体积不能装下第
01背包问题的状态转移方程
朴树版状态转移方程:
// 当前背包最大容量不能装下第i个物品,最大价值是第 i-1 个物品的集合 f[i][j] = f[i - 1][j]; if (j < v[i]) { // 当前背包最大容量能装下第i个物品,判断是选择1~(i-1)件物品的集合,还是选择1~i件物品的集合 f[i][j] = Math.max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]); }精华版状态转移方程:
f[j] = Math.max(f[j], f[j-v[i]] + w[i]);
?解题
?朴素版
之所以是朴素版是因为,代码有待优化,状态转移方程是二维的,空间复杂度较高。
时间复杂度:O ( N ∗ V ) O(N*V)O(N∗V);空间复杂度:O ( N ∗ V ) O(N*V)O(N∗V)。其中N是物品的数量,V是背包的容量。
代码:
import java.util.Scanner;
/**
* @title 0-1背包问题
* @author ghp
*
*/
public class Main {
public static void main(String[] args) {
// 接收输入
Scanner sc = new Scanner(System.in);
int N = sc.nextInt(); // 物品的数量
int V = sc.nextInt(); // 背包的容量
int[] v = new int[N + 1]; // 物品的体积
int[] w = new int[N + 1]; // 物品的价值
int[][] f = new int[N + 1][V + 1]; // 用于存储状态
for (int i = 1; i < N + 1; i++) {
v[i] = sc.nextInt();
w[i] = sc.nextInt();
}
// 循环遍历状态数组,利用状态转移方程不断更新状态,然后填充状态数组
// f[i][j]表示背包容量为j时,存放前i个物品的最优解
for (int i = 1; i < f.length; i++) {
for (int j = 1; j < f[i].length; j++) {
// 当前背包最大容量不能装下第i个物品,最大价值是第 i-1 个物品的集合
f[i][j] = f[i - 1][j];
if (j < v[i]) {
// 当前背包最大容量能装下第i个物品,判断是选择1~(i-1)件物品的集合,还是选择1~i件物品的集合
f[i][j] = Math.max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
}
}
}
// 测试:输出状态数组
for (int i = 1; i < f.length; i++) {
for (int j = 1; j < f[i].length; j++) {
System.out.print(f[i][j] + " ");
}
System.out.println();
}
// 输出得到背包能容纳的最大价值
System.out.println(f[N][V]);
}
}
测试结果:
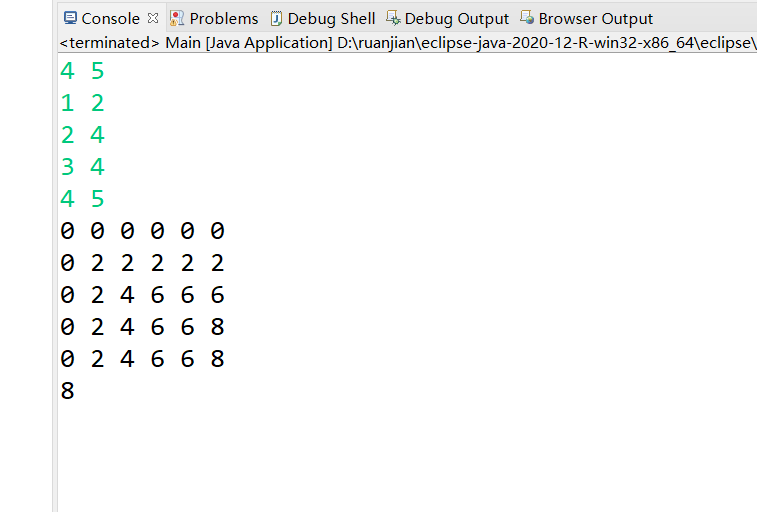
?精华版
之所以是精华版,是由于它在朴素版的基础上进行了优化,将二维的状态转移方程转换成了一维的状态转移方程。
时间复杂度:O ( N ∗ V ) O(N*V)O(N∗V);空间复杂度:O ( V ) O(V)O(V)。其中N是物品的数量,V是背包的容量。
这种方式虽然时间复杂度和和朴素版是一样的,但是更加省空间,它是通过类似于滚动数组的形式,不断循环利用状态数组,能够实现空间的复用。
PS:个人感觉这种方式比朴素版更加难以理解一点,所以一般情况下,我还是比较喜欢使用朴素版
代码:
import java.util.Scanner;
/**
* @title 完全背包问题
* @author ghp
*
*/
public class Main {
public static void main(String[] args) {
// 接收输入
Scanner sc = new Scanner(System.in);
int N = sc.nextInt(); // 物品的数量
int V = sc.nextInt(); // 背包的容量
int v[] = new int[N + 1]; // 物品的体积
int w[] = new int[N + 1]; // 物品的价值
int f[] = new int[V+1]; // 状态数组
for (int i = 1; i < N + 1; i++) {
v[i] = sc.nextInt();
w[i] = sc.nextInt();
}
// 填充状态数组
// 遍历物品
for (int i = 1; i <= N; i++) {
// 遍历背包的体积
for (int j = V; j >= v[i]; j--) {
f[j] = Math.max(f[j], f[j - v[i]] + w[i]);
}
}
// 测试: 打印状态数组
for (int i = 0; i < f.length; i++) {
System.out.print(f[i]+" ");
}
System.out.println();
// 输出背包能容纳的最大价值
System.out.print(f[V]);
}
}
注意:体积的遍历一定要按从大到小的顺序进行,因为
测试结果: