整数规划：
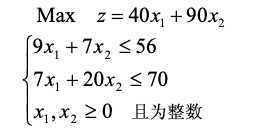
clc,clear;
c= [-40;-90];
A= [9 7;7 20];
b= [56;70];
lb= zeros(2,1);
[x,fval]= intlinprog(c,1:2,A,b,[],[],lb);
fval= -fval
x
分支定界法或者割平面法求解纯或者混合整数线性规划问题；
输出：
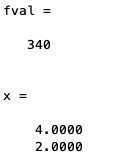
当条件A,B之间不是且关系而是或的时候：
固定成本问题(最优化函数中含有与xi无关的常量，相当于固定成本，优化函数可以写成总固定成本加上总可变成本之和)：
0-1整数规划问题(过滤隐枚举法，分枝隐枚举法)
指派问题(0-1规划特殊情形：匈牙利法)
蒙特卡洛法(求解各种类型规划)
下面主要介绍蒙特卡洛法(随机取样法)：
例题：
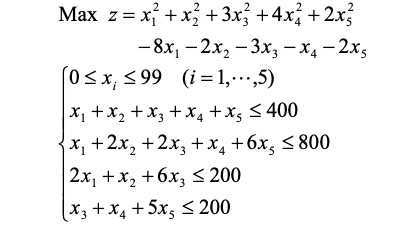
如果用显枚举法试探，需要计算1010个点，计算量巨大。但是用蒙特卡洛去计算106个点便可以找到满意解。
前提：整数规划的最优点不是孤立的奇点；
采集106个点后，我们有很大把握最优值点在106个点之中；
function [f,g] =mengte(x);
f= x(1)^2+x(2)^2+3*x(3)^2+4*x(4)^2+2*x(5)-8*x(1)-2*x(2)-3*x(3)-...
x(4)-2*x(5);
g= [sum(x)-400x(1)+2*x(2)+2*x(3)+x(4)+6*x(5)-800
2*x(1)+x(2)+6*x(3)-200x(3)+x(4)+5*x(5)-200];
rand(‘state‘,sum(clock));
p0= 0;
ticfor i = 1:10^6x= 99*rand(5,1);
x1=floor(x);
x2=ceil(x);
[f,g]=mengte(x1);if sum(g<=0)==4
if p0<=f
x0= x1;p0=f;
end
end
[f,g]=mengte(x2);if sum(g<=0)==4
if p0 <=f
x0=x2;
p0=f;
end
end
end
x0,p0
toc
输出：
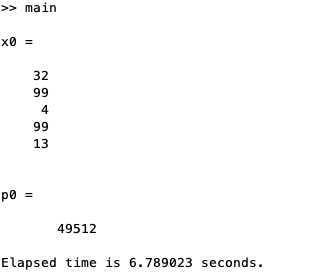
蒙特卡洛法得到的解为最优解的近似解，10^6个数据已经用了将近7s的时间，所以如果增加十倍，可能得70s时间才能得到结果。
蒙特卡洛法对计算器的计算能力要求很高。
lingo软件可以求得精确的全局最优解：
程序如下：
model:
sets: ！初始化变量集合；
row/1..4/:b; ！b为长度为4的行向量；
col/1..5/:c1,c2,x; ！c1,c2,x 为长度为5的列向量；
link(row,col):a; ！a为行列分别为4，5的系数矩阵；
endsets
data: ！实例化变量；
c1= 1,1,3,4,2c2= -8,-2,-3,-1,-2;
a= 1 1 1 1 1
1 2 2 1 6
2 1 6 0 0
0 0 1 1 5;
b= 400,800,200,200; ！满足a*x <= b;
enddata
max= @sum(col:c1*x^2+c2*x); !优化函数;
@for(row(i):@sum(col(j):a(i,j)*x(j))
@for(col:@gin(x)); ！产生随机的x;
@for(col:@bnd(0,x,99)); !x定义边界；
整数规划问题的求解可以使用Lingo等专用软件，对于一般的整数规划问题，无法直接利用matlab的函数；
必须利用Matlab编程实现分支定界解法和割平面解法。
对于指派问题等0-1整数规划问题，可以直接利用Matlab的函数intlinprog求解；
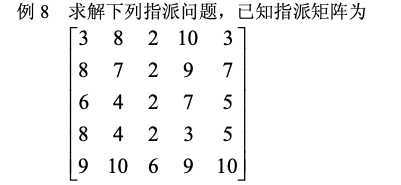
c=[3 8 2 10 3;8 7 2 9 7;6 4 2 7 5
8 4 2 3 5;9 10 6 9 10];
c=c(:);
a=zeros(10,25);for i=1:5a(i,(i-1)*5+(1:5))=1;
a(5+i,i:5:25)=1;
end
b=ones(10,1);
lb=zeros(25,1);
ub=ones(25,1);
[x,y]=intlinprog(c,(1:25),[],[],a,b,lb,ub);
x=reshape(x,[5,5]),y
所以 x15 = x23 = x32 = x44 = x51 = 1, 最优值为21
目标函数中含有分段线性函数时候如何求解问题呢？
可以看出最优化函数中含有分段线性函数c(x), 然后写出约束条件如下；
甲、乙两种汽油含有原油A的最低比例分别为0.5和0.6；
现在的问题关键在于如何处理分段线性函数c(x)。
可以有三种解决方法：
解法一：
非线性规划模型用Lingo软件更合适；
程序如下：
model: sets:
var1/1..4/:y; !这里y(1)=x11,y(2)=x21,y(3)=x12,y(4)=x22;
var2/1..3/:x,c;
endsets max=4.8*(y(1)+y(2))+5.6*(y(3)+y(4))[email protected](var2:c*x); y(1)+y(3)
y(2)+y(4)<1000;0.5*(y(1)-y(2))>0;0.4*y(3)-0.6*y(4)>0;
(x(1)-500)*x(2)=0;
(x(2)-500)*x(3)=0;
@for(var2:@bnd(0,x,500));
data:
c=10 8 6;
enddata
end
！可以用菜单命令“LINGO|Options”在“Global Solver”选项卡上启动全局优化选 型，并运行上述程序求得全局最有解:购买 1000 吨原油 A ，与库存的 500 吨原油 A 和 1000 吨原油 B 一起，共生产 2500 吨汽油乙，利润为 5000(千元)。;
解法二：
通过z1, z2, z3可以把x1, x2, x3限制在0到500之间，且满足x3 <= 500z3 <= x2 <= 500z2 <= x1 <= 500z1;
这种解法可以用matlab求解；
程序如下：
c = [4.8 5.6 4.8 5.6 0 -10 -8 -6 0 0 0]‘;
A = [1 1 0 0 -1 zeros(1,6); 0 0 1 1 zeros(1,7);0 0 0 0 1 zeros(1,6); -1 0 1 zeros(1,8);0 -2 0 3 zeros(1,7);
zeros(1,5) -1 0 0 0 500 0; zeros(1,5) 1 0 0 -500 0 0;
zeros(1,6) -1 0 0 0 500; zeros(1,6) 1 0 0 -600 0;
zeros(1,7) 1 0 0 -500];
b= [500 1000 1500 0 0 0 0 0 0 0]‘;
aeq = [zeros(1,4) -1 1 1 1 zeros(1,3)];
beq= [0]; %sum(x(6:8)) = x(5);
lb= zeros(11,1);
ub= [inf*ones(1,8) 1 1 1]‘;
[x, y] = intlinprog(-c,(1:11),A,b,aeq,beq,lb,ub);
format short g
x= x(1:5),y
输出为：
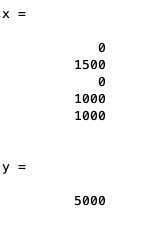
与解法一的结果一致。
解法三：将该分段函数直接画出来，可见：
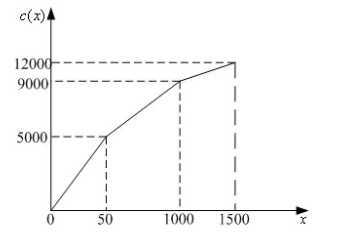其中50改成500。不等式(22)可以保证选择的那一段zi处的w满足要求。
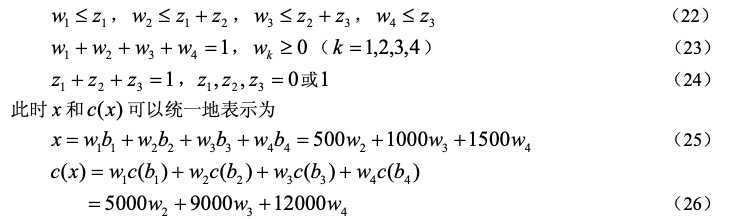
所以我们在x1 x2 x3 x4 x 上加了w1 w2 w3 w4 z1 z2 z3 其中z1 z2 z3为整数0-1，w1 w2 w3 w4为0~1之间的小数，与解法二相同，
也可以用matlab解出；但是这种方法多加了七个量，相对复杂，但是有一定的普遍性，所有含线性分段函数的整数线性规划问题均
可以用这种方法。
原文：https://www.cnblogs.com/raiuny/p/13068827.html