第九课遗传算法（ Genetic Algorithm, GA）

遗传算法概述

遗传算法（ Genetic Algorithm， GA）是一种进化算法，其基本原理是仿效生物界中的“物竞天择、适者生存” 的演化法则，它最初由美国Michigan大学的J. Holland教授于1967年提出。
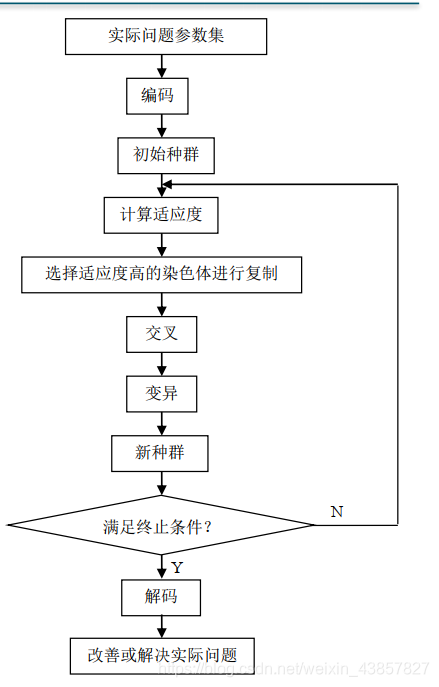
遗传算法是从代表问题可能潜在的解集的一个种群（ population）开始的，而一个种群则由经过基因（ gene）编码的一定数目的个体(individual)组成。因此，第一步需要实现从表现型到基因型的映射即编码工作。初代种群产生之后，按照适者生存和优胜劣汰的原理， 逐代（ generation）演化产生出越来越好的近似解，在每一代，根据问题域中个体的适应度(fitness)大小选择个体，借助于自然遗传学的遗传算子(genetic operators) 进行组合交叉和变异，产生出代表新的解集的种群。这个过程将导致种群像自然进化一样，后生代种群比前代更加适应于环境， 末代种群中的最优个体经过解码（ decoding），可以作为问题近似最优解。

GA三个基本操作：

选择（ Selection）、交叉（ Crossover）和变异（ Mutation）

（1）选择。选择的目的是为了从当前群体中选出优良的个体，使它们有机会作为父代为下一代繁衍子孙。根据各个个体的适应度值，按照一定的规则或方法从上一代群体中选择出一些优良的个体遗传到下一代种群中。选择的依据是适应性强的个体为下一代贡献一个或多个后代的概率大。（圆盘赌，将优良个体设置大区域）
（2）交叉。通过交叉操作可以得到新一代个体，新个体组合了父辈个体的特性。将群体中的各个个体随机搭配成对，对每一个个体，以交叉概率交换它们之间的部分染色体。
（3）变异。对种群中的每一个个体，以变异概率改变某一个或多个基因座上的基因值为其他的等位基因。同生物界中一样，变异发生的概率很低，变异为新个体的产生提供了机会。（与交叉相比，变异发生的概率比较低）

遗传算法的基本步骤：

编码： GA在进行搜索之前先将解空间的解数据表示成遗传空间的基因型串结构数据，这些串结构数据的不同组合便构成了不同的点。
初始群体的生成：随机产生N个初始串结构数据， 每个串结构数据称为一个个体， N个个体构成了一个群体。 GA以这N个串结构数据作为初始点开始进化。
适应度评估：适应度表明个体或解的优劣性。不同的问题，适应性函数的定义方式也不同。
选择：选择的目的是为了从当前群体中选出优良的个体，使它们有机会作为父代为下一代繁殖子孙。遗传算法通过选择过程体现这一思想，进行选择的原则是适应性强的个体为下一代贡献一个或多个后代的概率大。选择体现了达尔文的适者生存原则。
交叉：交叉操作是遗传算法中最主要的遗传操作。通过交叉操作可以得到新一代个体，新个体组合了其父辈个体的特性。交叉体现了信息交换的思想。
变异：变异首先在群体中随机选择一个个体，对于选中的个体以一定的概率随机地改变串结构数据中某个串的值。同生物界一样， GA中变异发生的概率很低，通常取值很小。

遗传算法工具箱

• MATLAB内嵌遗传算法工具箱: gadst
• Sheffield大学遗传算法工具箱: gatbx
• 北卡罗来纳大学遗传算法工具箱: gaot

本文使用gaot工具箱，下载地址
函数学习：
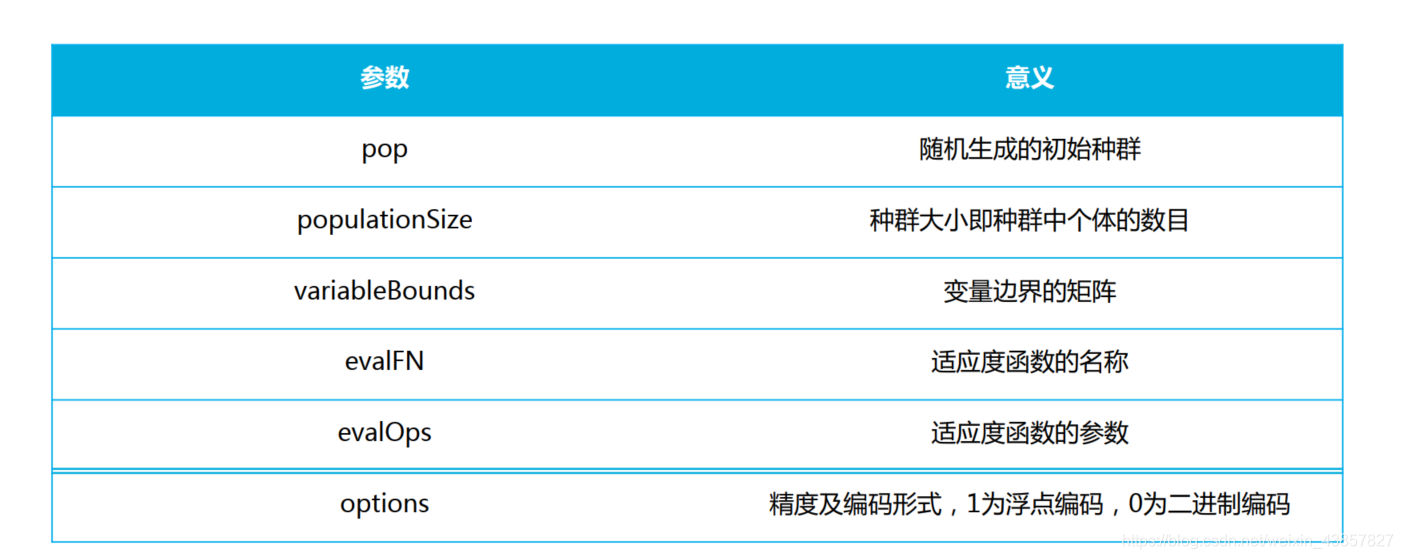
1、initializega

pop = initializega(populationSize,variableBounds,evalFN,evalOps,options)

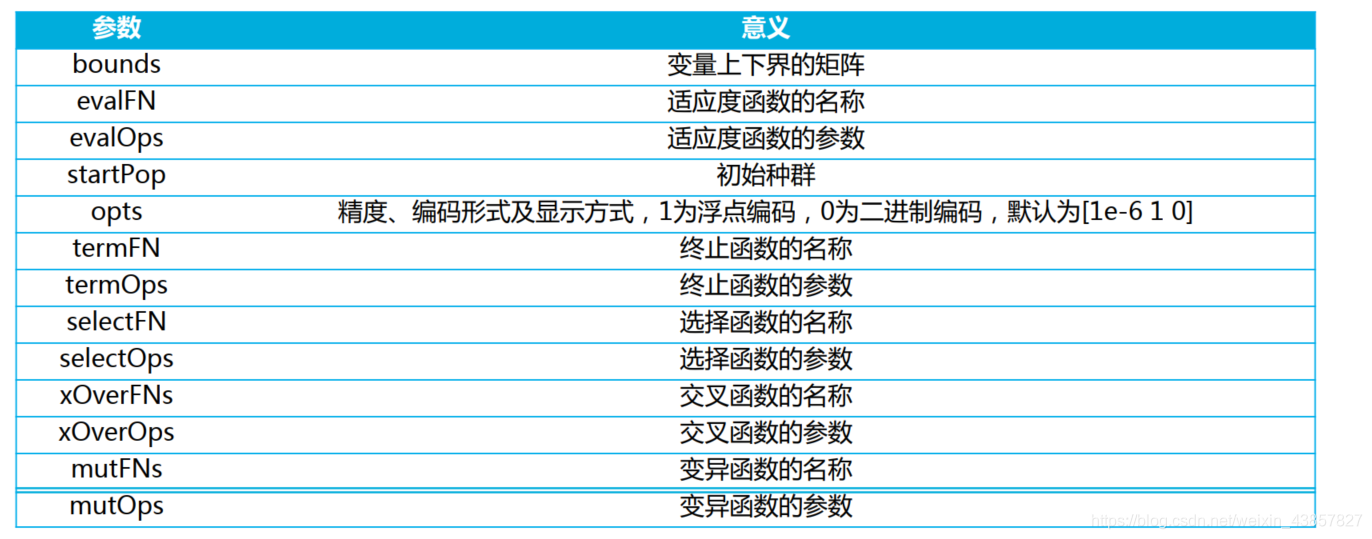
在这里插入图片描述
2、ga

[x,endPop,bPop,traceInfo] = ga(bounds,evalFN,evalOps,startPop,opts,termFN,termOps,selectFN,
selectOps,xOverFNs,xOverOps,mutFNs,mutOps)

在这里插入图片描述
输出参数：

案例分析

在这里插入图片描述
1、添加工具箱路径：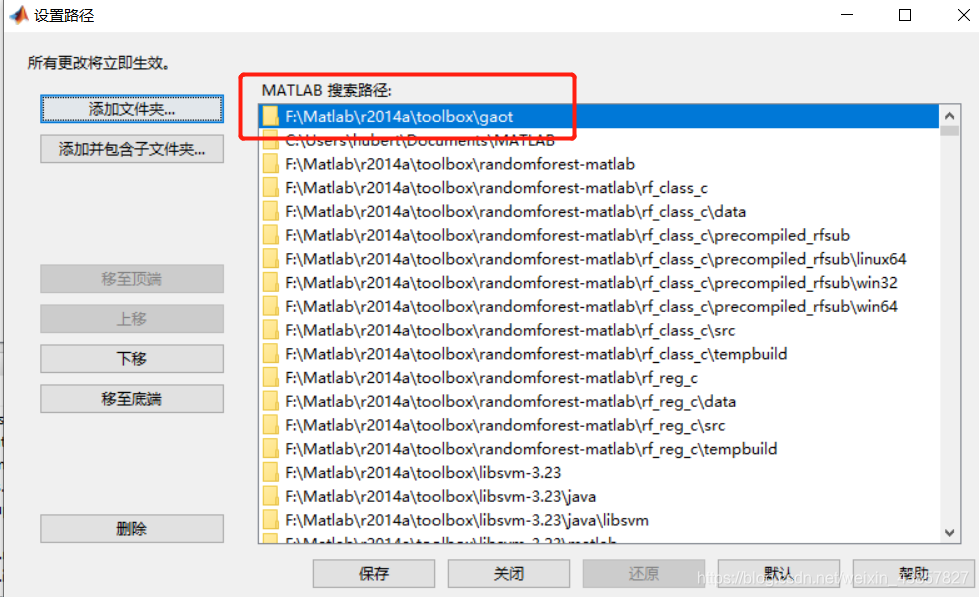

案例：一元函数优化

2、定义适应度函数fitness.m

function [sol, fitnessVal] = fitness(sol, options)

x = sol(1);

fitnessVal = x + 10*sin(5*x)+7*cos(4*x);  %求最大值
% fitnessVal = -1*(x + 10*sin(5*x)+7*cos(4*x));  %求最小值
end

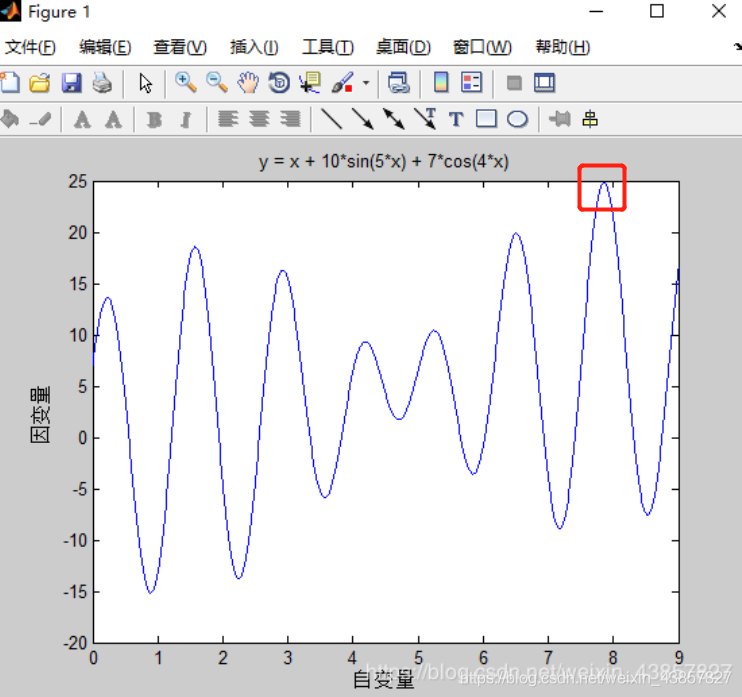
3、绘制函数曲线

%% II. 绘制函数曲线
x = 0:0.01:9;  %0-9步长为0.01  1*901
y =  x + 10*sin(5*x)+7*cos(4*x);  %1*901

figure
plot(x, y)
xlabel('自变量')
ylabel('因变量')
title('y = x + 10*sin(5*x) + 7*cos(4*x)')

在这里插入图片描述
4、初始化种群

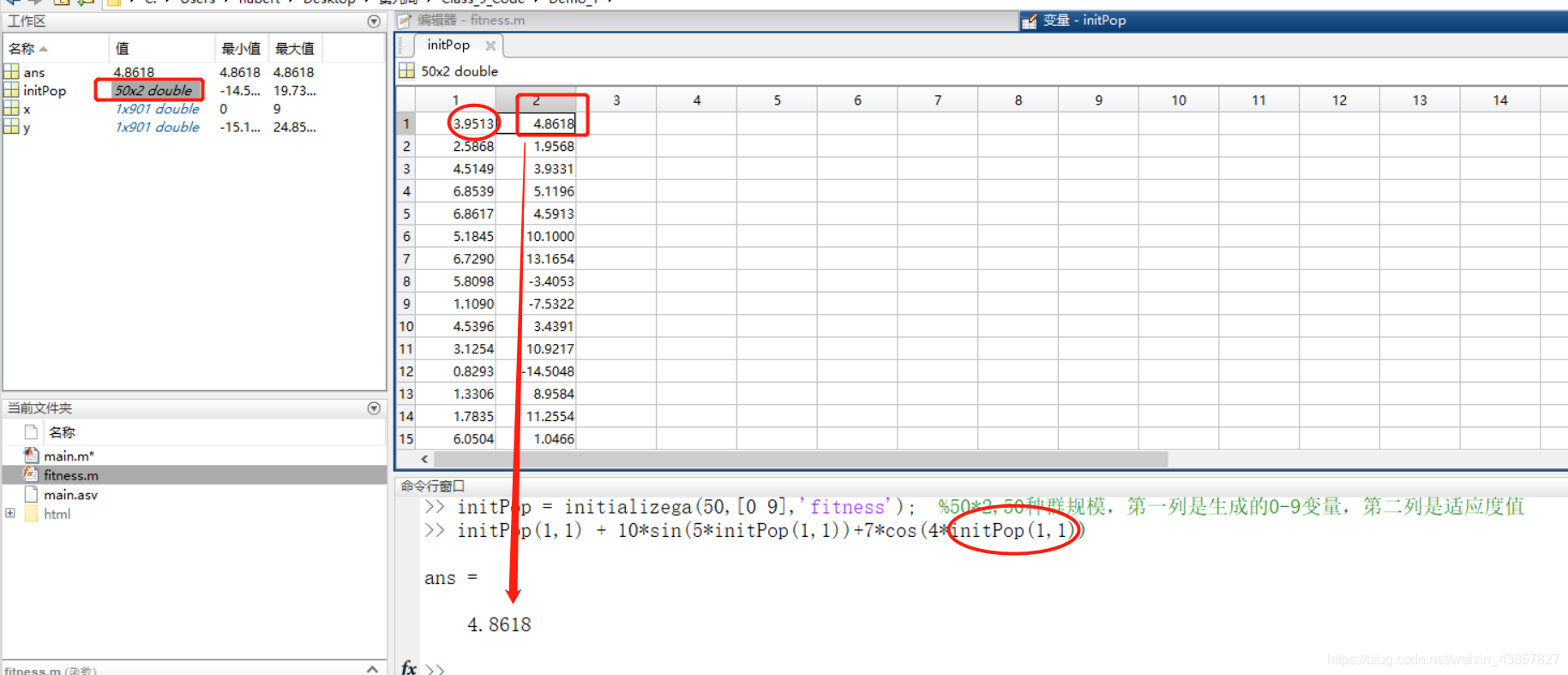
%% III. 初始化种群 50规模；范围0-9；适应度函数，默认为1浮点型
initPop = initializega(50,[0 9],'fitness');  %50*2,50种群规模，第一列是生成的0-9变量，第二列是计算的适应度值

在这里插入图片描述
5、遗传算法优化

%% IV. 遗传算法优化
% 参数：变量范围；适应度函数名称+参数[]；初始种群initPop;精度[1e-6 1 1]；最大迭代次数25；算子参数
[x endPop bpop trace] = ga([0 9],'fitness',[],initPop,[1e-6 1 1],'maxGenTerm',25,...
                           'normGeomSelect',0.08,'arithXover',2,'nonUnifMutation',[2 25 3]);


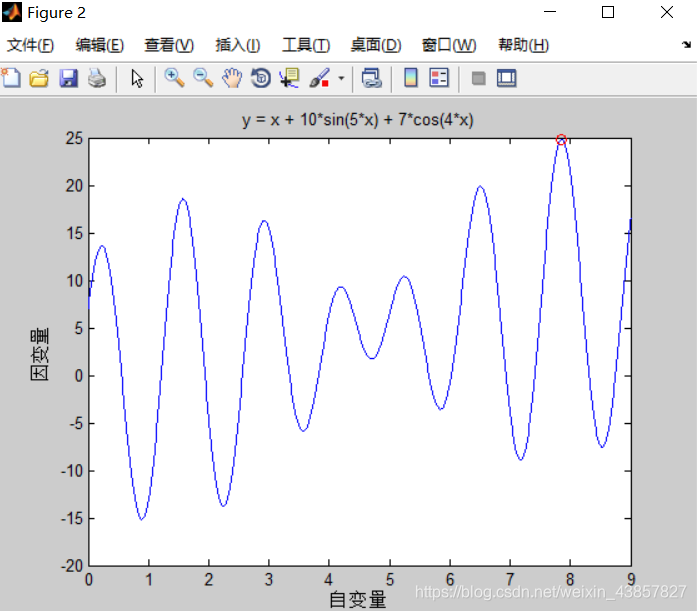
%% V. 输出最优解并绘制最优点
x
hold on
plot (endPop(:,1),endPop(:,2),'ro')  %第一列是个体，第二列是适应度函数值即y值

在这里插入图片描述

6、绘制迭代图像

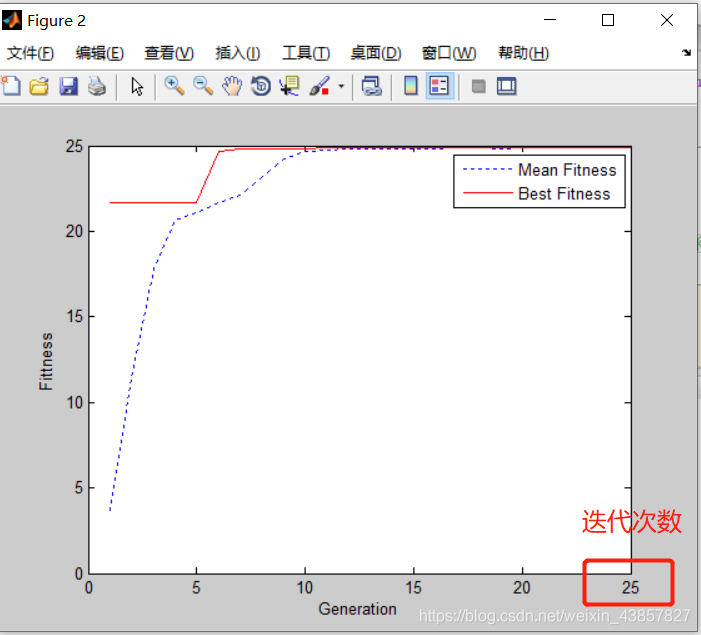
%% VI. 绘制迭代进化曲线
figure(2)
plot(trace(:,1),trace(:,3),'b:')
hold on
plot(trace(:,1),trace(:,2),'r-')
xlabel('Generation'); ylabel('Fittness');
legend('Mean Fitness', 'Best Fitness')

在这里插入图片描述

**案例：BP神经网络优化**

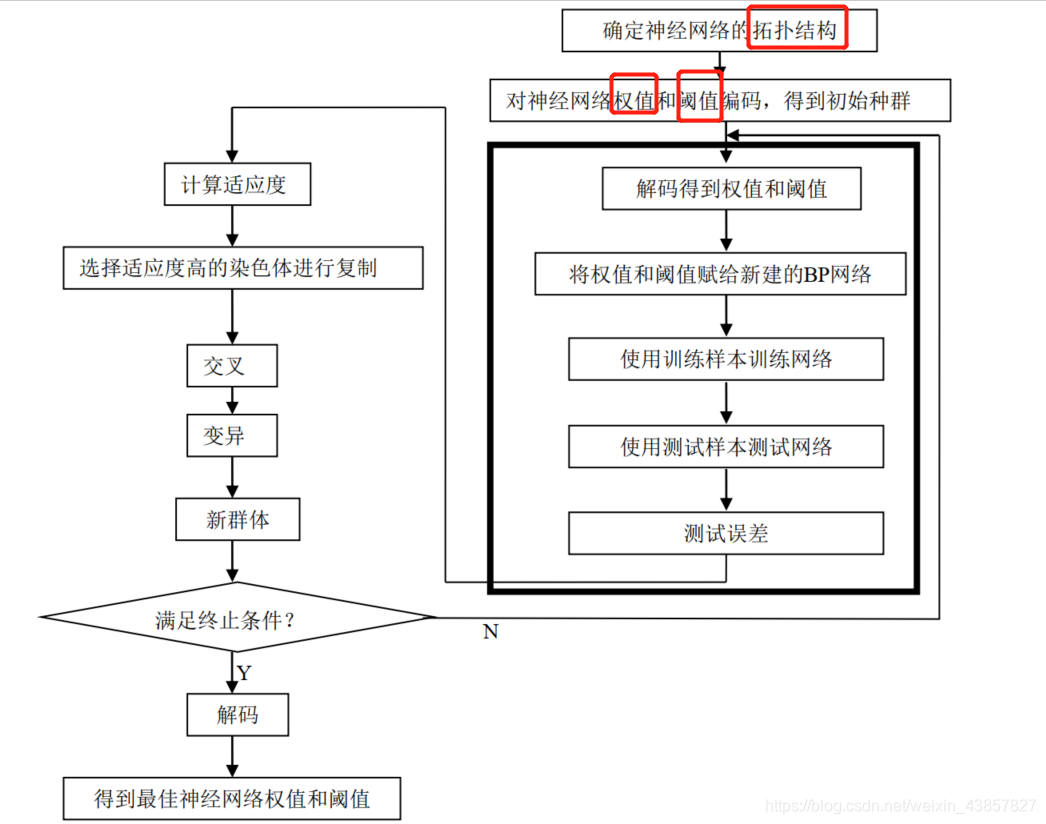
在这里插入图片描述
1、传统BP计算结果

%% I. 清除环境变量
clear all
clc

%% II. 声明全局变量
global p     % 训练集输入数据
global t     % 训练集输出数据
global R     % 输入神经元个数
global S2    % 输出神经元个数
global S1    % 隐层神经元个数
global S     % 编码长度
S1 = 10;

%% III. 导入数据
%%
% 1. 训练数据 输入6个变量，输出4个，4个样本，因此网络神经拓扑结构是6（输入）-10（神经元）-4（输出）
% 权值6*10+4*10=100，阈值10+4=14，因此编码长度S=114
p = [0.01 0.01 0.00 0.90 0.05 0.00;
     0.00 0.00 0.00 0.40 0.50 0.00;
     0.80 0.00 0.10 0.00 0.00 0.00;
     0.00 0.20 0.10 0.00 0.00 0.10]';
t = [1.00 0.00 0.00 0.00;
     0.00 1.00 0.00 0.00;
     0.00 0.00 1.00 0.00;
     0.00 0.00 0.00 1.00]';
%%
% 2. 测试数据
P_test = [0.05 0    0.9  0.12 0.02 0.02;
          0    0    0.9  0.05 0.05 0.05;
          0.01 0.02 0.45 0.22 0.04 0.06;
          0    0    0.4  0.5  0.1  0;
          0    0.1  0    0    0    0]';

%% IV. BP神经网络
%%
% 1. 网络创建
net = newff(minmax(p),[S1,4],{'tansig','purelin'},'trainlm'); 

%%
% 2. 设置训练参数
net.trainParam.show = 10;
net.trainParam.epochs = 2000;
net.trainParam.goal = 1.0e-3;
net.trainParam.lr = 0.1;

%%
% 3. 网络训练
[net,tr] = train(net,p,t);

%%
% 4. 仿真测试
s_bp = sim(net,P_test)    % BP神经网络的仿真结果

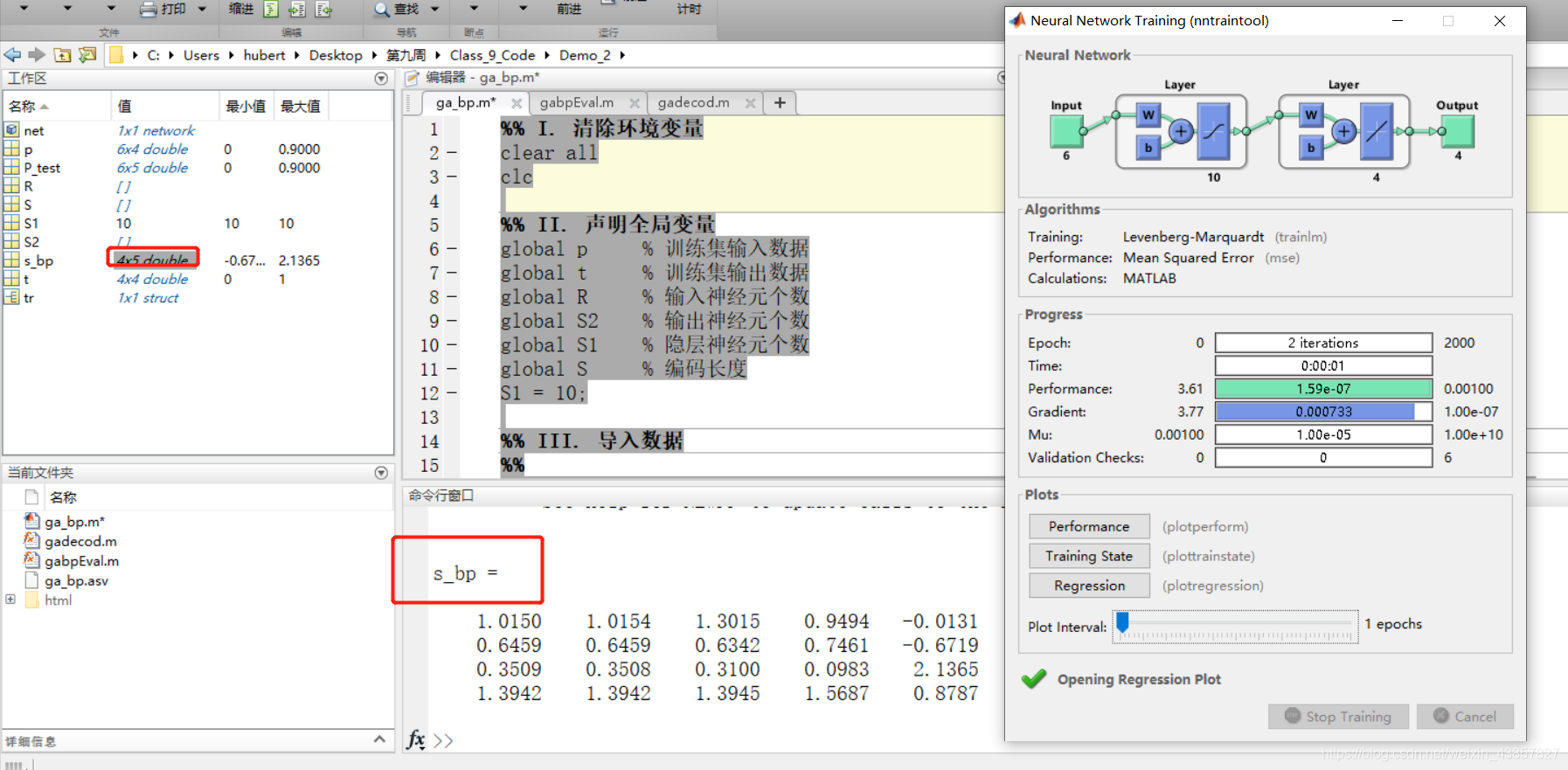
在这里插入图片描述
2、GA-BP神经网络
函数：
gabpEval.m

function[sol,val]=gabpEval(sol,options)
global S
for i=1:S
x(i)=sol(i);
end;
[W1,B1,W2,B2,val]=gadecod(x);

gadecod.m

function[W1,B1,W2,B2,val]=gadecod(x)
global p
global t
global R
global S2
global S1
% 前R*S1个编码为W1
for i=1:S1
    for k=1:R
        W1(i,k)=x(R*(i-1)+k);
    end
end
% 接着的S1*S2个编码(即第R*S1个后的编码)为W2
for i=1:S2
    for k=1:S1
        W2(i,k)=x(S1*(i-1)+k+R*S1);
    end
end
% 接着的S1个编码(即第R*SI+SI*S2个后的编码)为B1
for i=1:S1
    B1(i,1)=x((R*S1+S1*S2)+i);
end
%接着的S2个编码(即第R*SI+SI*S2+S1个后的编码)为B2
for i=1:S2
    B2(i,1)=x((R*S1+S1*S2+S1)+i);
end
% 计算S1与S2层的输出
A1=tansig(W1*p,B1);
A2=purelin(W2*A1,B2);
% 计算误差平方和
SE=sumsqr(t-A2);
% 遗传算法的适应值
val=1/SE;

整体代码：

%% V. GA-BP神经网络
% 1. 训练数据 输入6个变量，输出4个，4个样本，因此网络神经拓扑结构是6（输入）-10（神经元）-4（输出）
% 权值6*10+4*10=100，阈值10+4=14，因此编码长度S=114
R = size(p,1);
S2 = size(t,1);
S = R*S1 + S1*S2 + S1 + S2;
aa = ones(S,1)*[-1,1];

%% VI. 遗传算法优化
%%
% 1. 初始化种群
popu = 50;  % 种群规模  aa为范围-1-1；
initPpp = initializega(popu,aa,'gabpEval',[],[1e-6 1]);  % 初始化种群

%%
% 2. 迭代优化
gen = 100;  % 遗传代数
% 调用GAOT工具箱，其中目标函数定义为gabpEval
[x,endPop,bPop,trace] = ga(aa,'gabpEval',[],initPpp,[1e-6 1 1],'maxGenTerm',gen,...
                           'normGeomSelect',[0.09],['arithXover'],[2],'nonUnifMutation',[2 gen 3]);
%%
% 3. 绘均方误差变化曲线
figure(1)
plot(trace(:,1),1./trace(:,3),'r-');
hold on
plot(trace(:,1),1./trace(:,2),'b-');
xlabel('Generation');
ylabel('Sum-Squared Error');

%%
% 4. 绘制适应度函数变化
figure(2)
plot(trace(:,1),trace(:,3),'r-');
hold on
plot(trace(:,1),trace(:,2),'b-');
xlabel('Generation');
ylabel('Fittness');

%% VII. 解码最优解并赋值
%%
% 1. 解码最优解
[W1,B1,W2,B2,val] = gadecod(x);

%%
% 2. 赋值给神经网络
net.IW{1,1} = W1;
net.LW{2,1} = W2;
net.b{1} = B1;
net.b{2} = B2;

%% VIII. 利用新的权值和阈值进行训练
net = train(net,p,t);

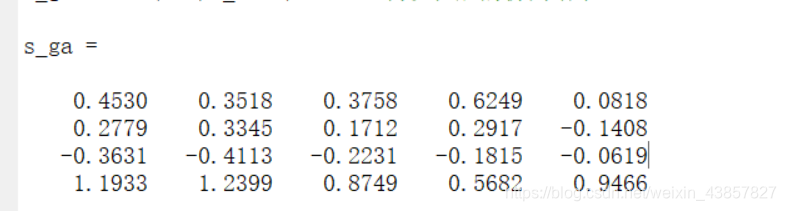
%% IX. 仿真测试
s_ga = sim(net,P_test)    %遗传优化后的仿真结果

在这里插入图片描述

原文链接：https://blog.csdn.net/weixin_43857827/article/details/103057609