刚体运动学公式_物理-力学|第一讲|质点运动学

质点模型

当研究对象本身的几何形状对力学运动过程的影响可忽略不计时，仅保留对象的质量，将对象的几何形状退化成“点”所得到的模型就是质点模型。比如当我们描述地球绕太阳运动这一过程时，太阳和地球的几何形状都是可以忽略不计的，故通常把太阳和地球都看成是质量集中于一点的质心；再比如做一个单摆实验，当绳长远大于小球的直径时（比如说一百倍），我们也可以将小球的直径忽略掉，但是其实由此也产生了误差，因为小球刚体绕其自身转动的能量被忽略掉了，在以后的刚体一讲中，我们将会详细讨论刚体转动的能量。

运动的描述

选定空间中一点，可以引入位置矢量

来描述任意时刻t质点在空间中的位置，该矢量从定点出发，指向质点所在位置。由此可以得到质点在任意时刻t的速度

以及任意时刻的加速度

。

有时候需要讨论一个质点相对于另一个质点的运动情况，通过一个质点与另一个质点的相对位置矢量对时间求导，可以得到两个质点间的相对速度和相对加速度。

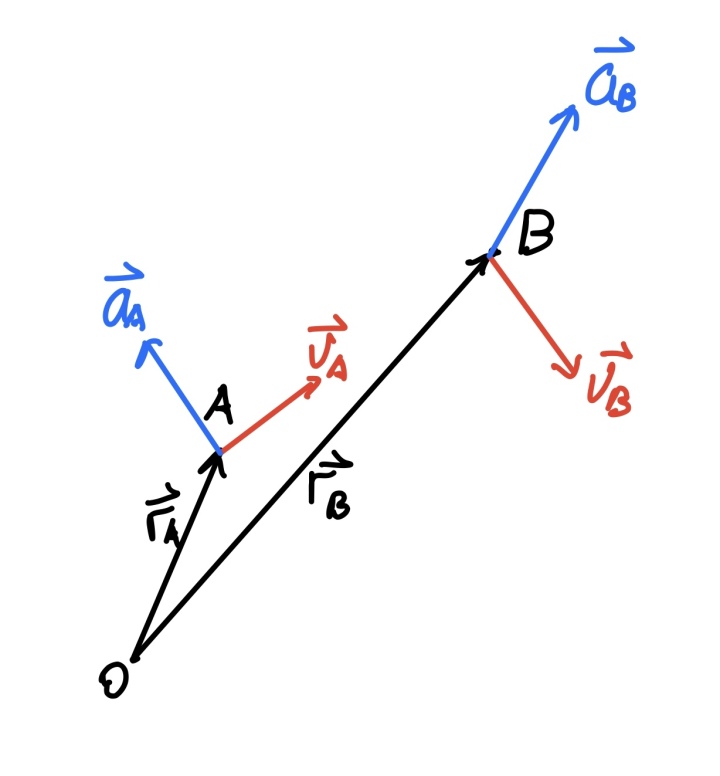
相对运动的概念是十分重要的，因为在不同的参考系下，同意运动过程可能呈现出不同的形式，其数学表达也将有简单与复杂的差异。比如在不同时刻以不同初速度竖直上抛两个小球，在地面系两个小球各自先加速后减速，而在自由落体系（观察者从楼上跳下来，与两个小球一起自由落体），两个小球各自以一定速度做匀速直线运动，而其相对速度即为其初速度之差。

角量

取定空间中的一点O，我们还可以通过质点与定点O的连线的转动情况来“部分地”描述质点在空间中的运动，以某一时刻连线位置为基准，任意时刻连线相对于基准连线的角度记为

，方向满足右手法则，进而得到任意时刻质点相对O的角速度

，以及任意时刻质点相对O的角加速度

。角量与速度以及加速度的"一个分量"之间存在关系 如下：

角量对于一个具有一定圆周运动性质的运动过程的描述具有“优势”。

坐标系下的质点运动描述

接下来具体讨论质点在直角坐标系、极坐标系以及自然坐标系下的运动描述。

1、直角坐标系

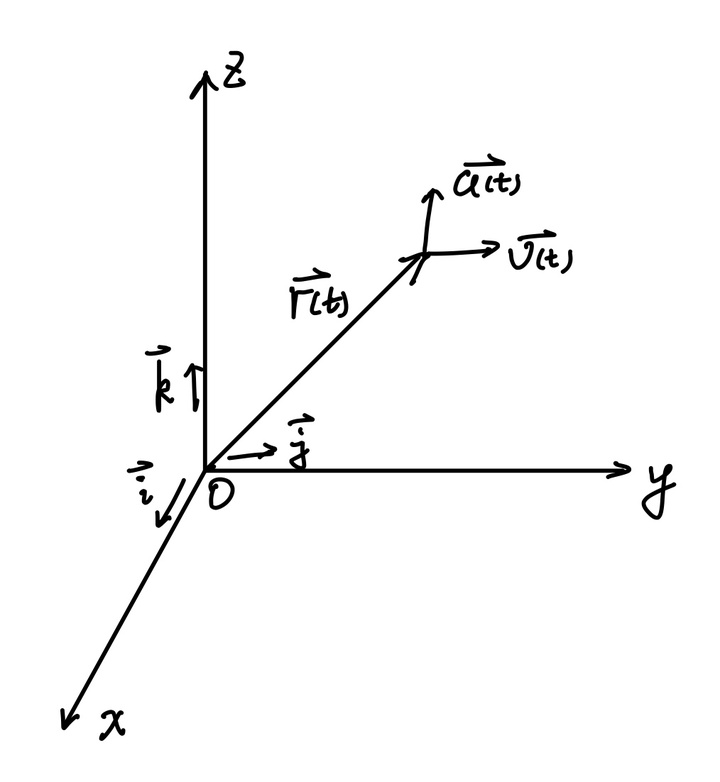
在直角坐标系下，质点运动方程比较显然：

2、极坐标系

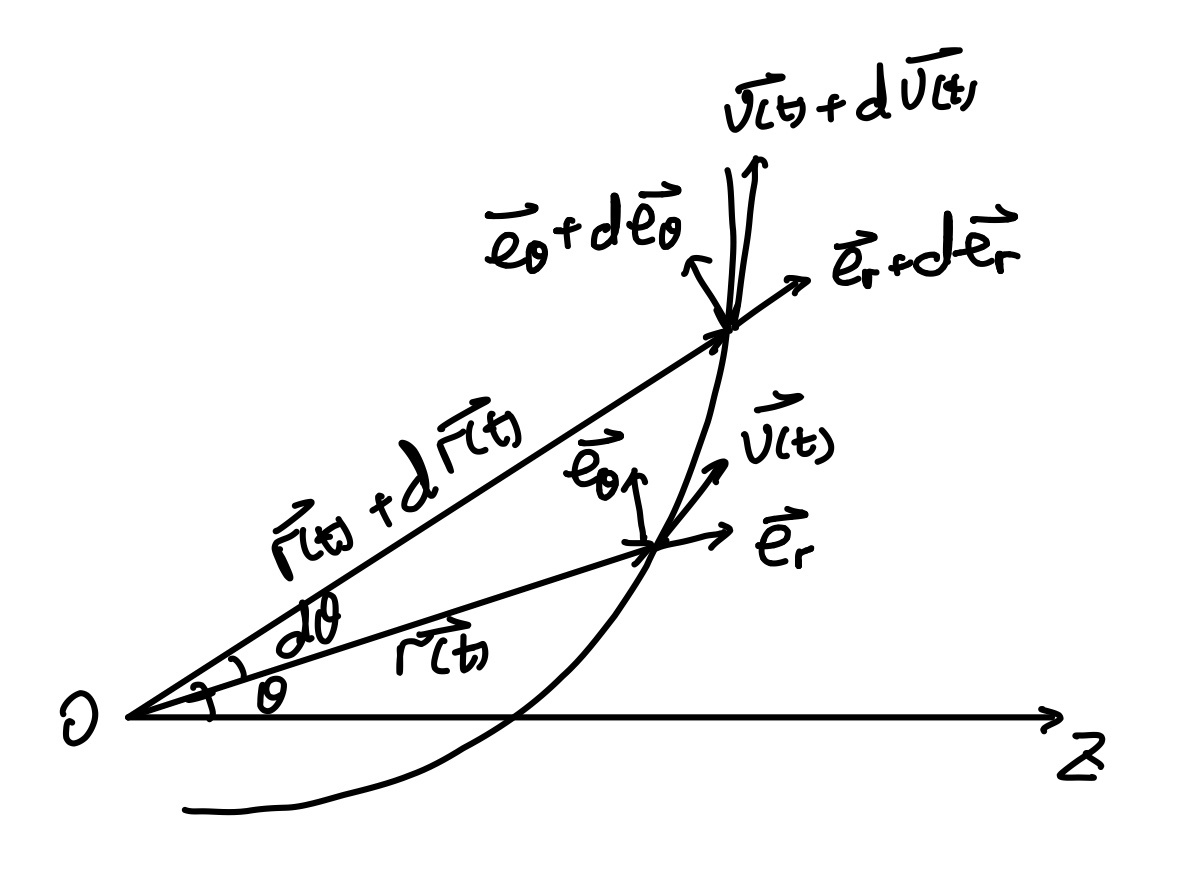
极坐标系与直角坐标系的最大的区别在于前者的单位向量

和

会随着质点的运动而发生变化，而后者不会，因而在极坐标系下的运动方程对时间求导时两个单位向量也要对时间求导。下面我们先考察两个单位向量对时间的导数。

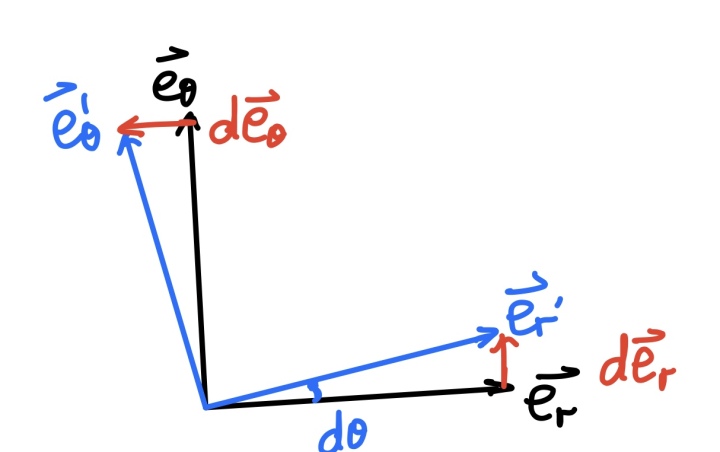
从几何的关系通过近似得到两个单位向量对时间的导数如下：

接下来就可以通过位置矢量对时间求导的办法得到速度矢量和加速度矢量：

一般极坐标用于描述有心运动过程（如天体的运动），当我们之后讲到非惯性系时，极坐标还可以从一种特殊的转动系的角度来理解。
3、自然坐标系

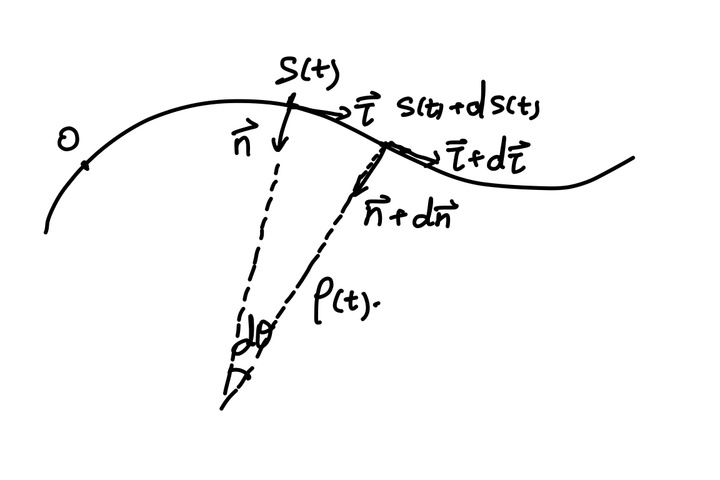
自然坐标系是在质点运动轨迹已知的条件下建立的一种依赖于质点运动轨迹的坐标系，记零时刻质点所在位置为原点O，只要知道任意时刻质点所运动的路程S(t)，即可完全描述质点的运动状态。在自然坐标系下引入了一个新的量——曲率半径

。在数学上，曲率半径是空间曲线的性质之一，描述了曲线在某一点的弯曲程度，通常在知道曲线解析式的情况下可以通过曲率公式直接求得曲线在某一点得曲率半径；在物理学上，质点的曲线运动可以近似成无穷多个圆弧运动的叠加，质点在每一时刻以某一半径某一角速度做圆弧运动，该半径就称为曲率半径，显然物理学中曲率半径可以是时间的函数。

与极坐标类似的，自然坐标的单位向量也不是固定不变的，故而也应考虑其对时间的导数，但是由于自然坐标中

始终与速度垂直，故在推导中不涉及其对时间的导数，只需考虑

对时间的导数。

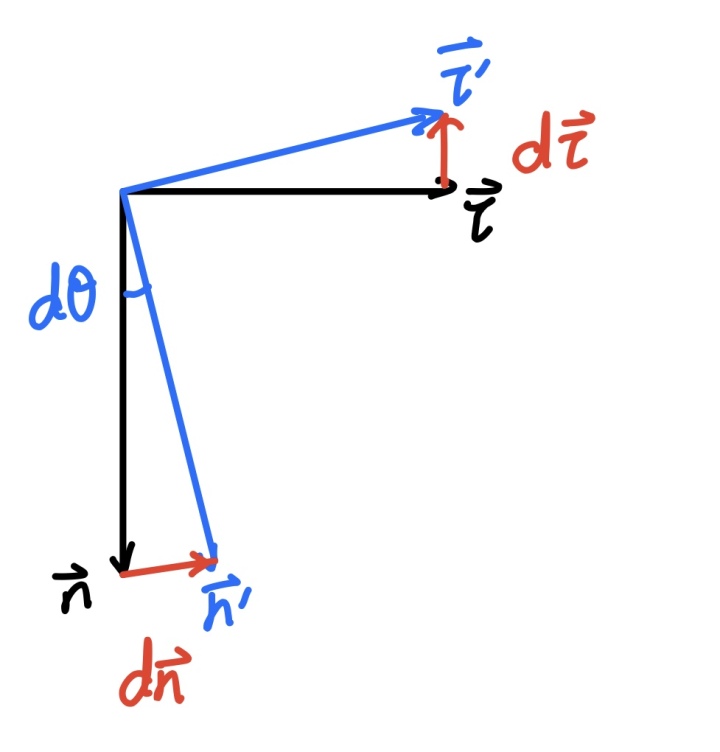
接下来就可表示出速度、加速度关于时间的函数：

小结

本讲首先引入了质点模型，阐述了对质点运动进行数学描述的基本方法，给出了两质点间相互运动的关系，并且在三种坐标系下推导了其运动学方程的具体形式。