Java-算法-分治

一. 分治简单介绍

        分治可以把总的大的问题拆成一个一个小问题，在小问题中仍然可以继续分成小的问题，个人认为和递归相比最重要的区别是，有没有分“左”和“右”，即拆成的左和右是否又都进行了同样的递归从而形成左和右加起来就可以形成整个问题的答案。

二. leetcode实战

(1) 例一

leetcode240

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

输入：matrix = [[1, 4,   7,  11,   15],

                         [2, 5,   8,   12,   19],

                         [3, 6,   9,   16,   22],

                        [10,13,14,  17,   24],

                        [18,21,23,  26,   30]],

target = 5
输出：true

输入：matrix = [[1,4,7,11,15],

                        [2,5,8,12,19],

                        [3,6,9,16,22],

                        [10,13,14,17,24],

                        [18,21,23,26,30]],

target = 20
输出：false

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        for(int[] arr : matrix){
            int index = search(arr,target);
            if(index >=0){
                return true;
            }
        }
        return false;
    }

    public int search(int[] arr,int target){
        int L = 0;
        int R = arr.length-1;
        while(L <= R){
            int mid =L+((R-L)>>1);
            if(arr[mid] == target){
                return 1;
            }
            else if(arr[mid] > target){
                R = mid -1;
            }
            else{
                L = mid +1;
            }
        }
        return -1;
    }
}

(2) 例二

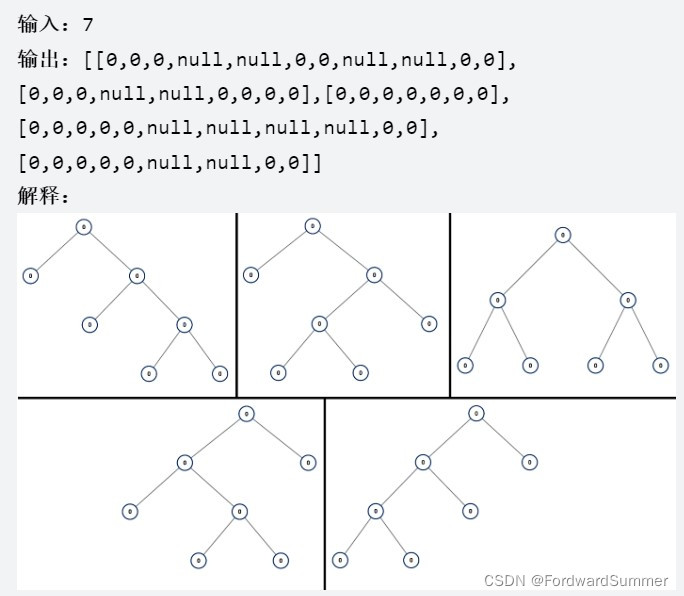
leetcode894所有可能的二叉树

满二叉树是一类二叉树，其中每个结点恰好有 0 或 2 个子结点。返回包含 N 个结点的所有可能满二叉树的列表。 答案的每个元素都是一个可能树的根结点。答案中每个树的每个结点都必须有 node.val=0。你可以按任何顺序返回树的最终列表。

class Solution{
    public List<TreeNode> allPossibleFBT(int n){
        List<TreeNode> list =  new ArrayList<>();
        if(n == 1){
            list.add(new TreeNode(0));
            return list;
        }
        for(int i = 1; i < n-1; i=i+2){
            List<TreeNode> leftlist = allPossibleFBT(i);
            List<TreeNode> rightlist =allPossibleFBT(n-i-1);
            for(int left = 0; left < leftlist.size(); left++){
                for(int right = 0; right < rightlist.size(); right++){
                    TreeNode cur = new TreeNode(0);
                    cur.left = leftlist.get(left);
                    cur.right = rightlist.get(right);
                    list.add(cur);
                }
            }
        }
        return list;
    }
}

(3) 例三

leetcode241为运算表达式设计运算符

给你一个由数字和运算符组成的字符串 expression ，按不同优先级组合数字和运算符，计算并返回所有可能组合的结果。你可以 按任意顺序 返回答案。

输入：expression = "2-1-1"
输出：[0,2]
解释：
((2-1)-1) = 0 
(2-(1-1)) = 2

输入：expression = "2*3-4*5"
输出：[-34,-14,-10,-10,10]
解释：
(2*(3-(4*5))) = -34 
((2*3)-(4*5)) = -14 
((2*(3-4))*5) = -10 
(2*((3-4)*5)) = -10 
(((2*3)-4)*5) = 10

class Solution {
    public List<Integer> diffWaysToCompute(String expression) {
        List<Integer> list = new ArrayList<>();
        for(int i = 0; i < expression.length(); i++){
            char temp = expression.charAt(i);
            if( temp == '+' ||  temp == '-'||  temp == '*'){
                List<Integer> left =  diffWaysToCompute(expression.substring(0,i));
                List<Integer> right =  diffWaysToCompute(expression.substring(i+1));
                for(int k : left ){
                    for(int s : right){
                        if(temp == '+'){
                            list.add(k+s);
                        }
                        if(temp == '-'){
                            list.add(k-s);
                        }
                        if(temp == '*'){
                            list.add(k*s);
                        }
                    }
                }
            }    
        }
        if(list.size() == 0){
            list.add(Integer.parseInt(expression));
        }
        return list;
    }
}