本文介绍了重要性采样(Importance Sampling)并给出了示例。
本文篇幅较长,分为以下几个部分:
- 重要性采样是什么
- 重要性采样的应用示例
- 不同的分布Q QQ对结果有影响吗?
- 小结和附录代码
Part1:重要性采样是什么
前文《R-概率统计与模拟(三)变换均匀分布对特定分布进行抽样》和《R-概率统计与模拟(四)拒绝抽样》分别介绍了两种方法,可以根据已知的p.d.f.进行采样(抽样),使得采样得到的点符合目标分布。“重要性抽样”(Importance Sampling)不同于上述两种方法,其主要用途是通过采样计算数学期望。 而这与积分的计算有关。
通过大量随机采样计算积分
在建模过程中,我们经常要计算某个函数的期望:假设变量X XX符合某个分布P PP,记为X ∼ P X \sim PX∼P,其p.d.f. \text{p.d.f.}p.d.f.记为p ( x ) p(x)p(x)。我们想要计算某个函数f ff在分布P PP下的期望E [ f ( X ) ] E[f(X)]E[f(X)]。根据期望的数学定义,我们知道:
E X ∼ P [ f ( X ) ] = ∫ x f ( x ) p ( x ) d x E_{X \sim P}[f(X)] = \int_x f(x)p(x) \, \text{d}xEX∼P[f(X)]=∫xf(x)p(x)dx
在实际操作中,往往上面积分的解析解很难计算,所以可以通过大量采样的方法进行近似计算:假设根据分布P PP进行大量随机采样,样本量记为N NN,样本点记为{ x ^ 1 , x ^ 2 , … , x ^ N } \{\hat{x}_1, \hat{x}_2, \ldots, \hat{x}_N \}{x^1,x^2,…,x^N},那么当N NN足够大时,
E X ∼ P [ f ( X ) ] = ∫ x f ( x ) p ( x ) d x ≈ 1 N ∑ i = 1 N f ( x ^ i ) E_{X \sim P}[f(X)] = \int_x f(x)p(x) \, \text{d}x \approx \frac{1}{N} \sum_{i=1}^{N} f(\hat{x}_i)EX∼P[f(X)]=∫xf(x)p(x)dx≈N1i=1∑Nf(x^i)
所以关键在于如何对分布P PP进行采样。当然我们可以根据前文介绍的“变换均匀分布进行抽样”或者“拒绝抽样”的方法进行采样。但是,如前文所说,这两种方法都有局限。当遇到一个复杂的p.d.f. \text{p.d.f.}p.d.f.时,两种方法可能都不适用。
引入另一个分布Q QQ
当无法直接对分布P PP进行采样从而难以近似计算上述积分时,我们可以对上面的积分做一个变换(即“重要性采样”的关键部分),让计算变得简单可行:
我们选取另一个容易进行抽样的分布Q QQ,其p.d.f. \text{p.d.f.}p.d.f.记为q ( x ) q(x)q(x)。上述积分变换为:
E X ∼ P [ f ( X ) ] = ∫ x f ( x ) p ( x ) d x = ∫ x f ( x ) p ( x ) q ( x ) q ( x ) dx E_{X \sim P}[f(X)] = \int_x f(x)p(x) \, \text{d}x = \int_x f(x) \frac{p(x)}{q(x)} q(x) \, \text{dx}EX∼P[f(X)]=∫xf(x)p(x)dx=∫xf(x)q(x)p(x)q(x)dx
然后我们根据分布Q QQ进行大量随机采样,样本量记为N NN,样本点记为{ x 1 , x 2 , … , x N } \{x_1, x_2, \ldots, x_N \}{x1,x2,…,xN},那么当N NN足够大时,
E X ∼ P [ f ( X ) ] = ∫ x f ( x ) p ( x ) d x = ∫ x f ( x ) p ( x ) q ( x ) q ( x ) dx ≈ 1 N ∑ i = 1 N p ( x i ) q ( x i ) f ( x i ) E_{X \sim P}[f(X)] = \int_x f(x)p(x) \, \text{d}x = \int_x f(x) \frac{p(x)}{q(x)} q(x) \, \text{dx} \approx \frac{1}{N} \sum_{i=1}^{N} \frac{p(x_i)}{q(x_i)} f(x_i)EX∼P[f(X)]=∫xf(x)p(x)dx=∫xf(x)q(x)p(x)q(x)dx≈N1i=1∑Nq(xi)p(xi)f(xi)
相比较于原来的计算方式,变换后的式子中p ( x i ) q ( x i ) \frac{p(x_i)}{q(x_i)}q(xi)p(xi)就是加之于f ( x i ) f(x_i)f(xi)的权重(重要性)。
简单小结
小结一下,要计算分布P PP下的数学期望E [ f ( X ) ] E[f(X)]E[f(X)],重要性采样主要分为以下两步:
- 选取另一个容易直接采样的分布Q QQ,并据此分布大量随机采样,得到一系列采样点{ x 1 , x 2 , … , x N } \{x_1, x_2, \ldots, x_N \}{x1,x2,…,xN}
- 根据上面的采样点,计算1 N ∑ i = 1 N p ( x i ) q ( x i ) f ( x i ) \frac{1}{N} \sum_{i=1}^{N} \frac{p(x_i)}{q(x_i)} f(x_i)N1∑i=1Nq(xi)p(xi)f(xi)的值作为近似结果。
Part2:重要性采样的应用示例
为了验证重要性采样的可行性,本文列举了两个示例,分别是计算均匀分布和非对称拉普拉斯分布的数学期望。(注意,这两个示例本身都可以直接计算出数学期望的理论值,用它们做例子只是为了验证重要性采样是否可以得到正确的结果。)
首先看均匀分布的例子:假设变量X ∼ U ( 0 , 1 ) X \sim \text{U}(0,1)X∼U(0,1),试计算E [ X ] E[X]E[X]和E [ X 2 ] E[X^2]E[X2]。
很明显,上述两个期望的理论值是:
E T [ X ] = 0.5 , E T [ X 2 ] = 1 3 E_T[X]=0.5, \quad E_T[X^2]=\frac{1}{3}ET[X]=0.5,ET[X2]=31
其中T TT表示理论值(Theoretical Value)。
接下来我们需要看看利用重要性采样的方法是否可以得到正确的结果:分布P PP是简单的均匀分布,我们选取另一个简单的分布Q QQ来进行采样,二者的p.d.f. \text{p.d.f.}p.d.f.如下:
p ( x ) = 1 , x ∈ [ 0 , 1 ] q ( x ) = 2 x , x ∈ [ 0 , 1 ] \begin{aligned} & p(x) = 1, \quad \ \ x \in [0,1] \\ & q(x) = 2x, \quad x \in [0,1] \end{aligned}p(x)=1, x∈[0,1]q(x)=2x,x∈[0,1]
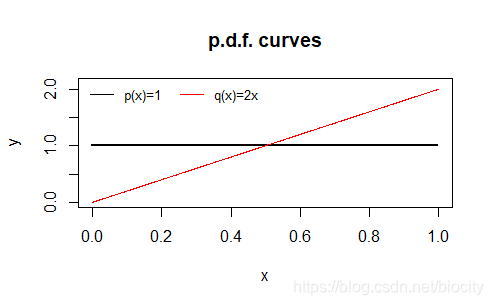
我们可以利用“变换均匀分布”的方法对分布Q QQ进行采样,当采样点的数量达到10万个时,结果是:
E Q [ X ] = 1 N ∑ i = 1 N p ( x i ) q ( x i ) x i = 0.5 , E Q [ X 2 ] = 1 N ∑ i = 1 N p ( x i ) q ( x i ) x i 2 = 0.3331424 \begin{aligned} E_Q[X] & = \frac{1}{N} \sum_{i=1}^{N} \frac{p(x_i)}{q(x_i)} x_i =0.5, \\ E_Q[X^2] &= \frac{1}{N} \sum_{i=1}^{N} \frac{p(x_i)}{q(x_i)} x_i^2 =0.3331424 \end{aligned}EQ[X]EQ[X2]=N1i=1∑Nq(xi)p(xi)xi=0.5,=N1i=1∑Nq(xi)p(xi)xi2=0.3331424
与真实值非常接近。说明采用分布Q QQ进行重要性采样是有效的。(这一示例的R代码见文末“代码段C1”。)
其次看一个非对称拉普拉斯分布的例子:假设变量X ∼ AL ( μ , σ , p ) X \sim \text{AL}(\mu,\sigma,p)X∼AL(μ,σ,p),试计算E [ X ] E[X]E[X]和E [ X 2 ] E[X^2]E[X2]。
本文所使用的非对称拉普拉斯分布(Asymmetric Laplace Distribution)具有如下p.d.f. \text{p.d.f.}p.d.f.:
p ( x ) = f ( x ; μ , σ , p ) = p ( 1 − p ) σ exp ( − x − μ σ [ p − I ( x ≤ μ ) ] ) p(x)=f(x;\mu,\sigma,p)=\frac{p(1-p)}{\sigma} \exp \left(-\frac{x-\mu}{\sigma} [p - I(x \le \mu)] \right)p(x)=f(x;μ,σ,p)=σp(1−p)exp(−σx−μ[p−I(x≤μ)])
其中,0 < p < 1 0<p<10<p<1,σ > 0 \sigma > 0σ>0,− ∞ < μ < ∞ -\infty < \mu < \infty−∞<μ<∞,I ( ⋅ ) I(\cdot)I(⋅)是指示函数。和上面均匀分布相比,这个分布复杂了很多。根据文献[1](Keming Yu & Jin Zhang, 2006),若X ∼ AL ( μ , σ , p ) X \sim \text{AL}(\mu,\sigma,p)X∼AL(μ,σ,p),则上述期望的理论值是:
E T [ X ] = μ + σ ( 1 − 2 p ) p ( 1 − p ) , E T [ X 2 ] = σ 2 ( 1 − 2 p + 2 p 2 ) ( 1 − p ) 2 p 2 + E T 2 [ X ] E_T[X]=\mu + \frac{\sigma(1-2p)}{p(1-p)}, \quad E_T[X^2]=\frac{\sigma^2(1-2p+2p^2)}{(1-p)^2p^2} + E_T^2[X]ET[X]=μ+p(1−p)σ(1−2p),ET[X2]=(1−p)2p2σ2(1−2p+2p2)+ET2[X]
其中T TT表示理论值。
我们以μ = 1 , σ = 0.5 , p = 0.2 \mu=1, \sigma=0.5, p=0.2μ=1,σ=0.5,p=0.2,即X ∼ AL ( 1 , 0.5 , 0.2 ) X \sim \text{AL}(1, 0.5, 0.2)X∼AL(1,0.5,0.2)为例,根据上面的公式,期望的理论值是:
E T [ X ] = 2.875 , E T [ X 2 ] = 14.90625 E_T[X]=2.875, \quad E_T[X^2]=14.90625ET[X]=2.875,ET[X2]=14.90625
接下来我们选择正态分布N ( E T [ X ] , Var ( X ) ) \text{N}(E_T[X], \sqrt{\text{Var}(X)})N(ET[X],Var(X))作为分布Q QQ进行重要性采样。其中,Var ( X ) = σ 2 ( 1 − 2 p + 2 p 2 ) ( 1 − p ) 2 p 2 \text{Var}(X)=\frac{\sigma^2(1-2p+2p^2)}{(1-p)^2p^2}Var(X)=(1−p)2p2σ2(1−2p+2p2)。我们将两个分布的p.d.f. \text{p.d.f.}p.d.f.曲线放在一起比较一下: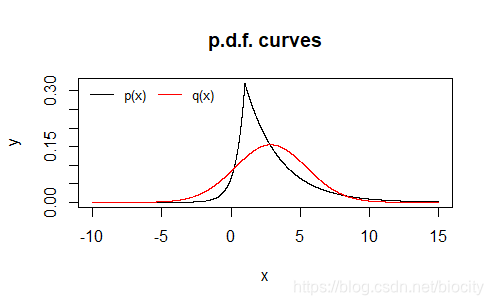
为什么选择正态分布作为分布Q QQ,一是正态分布采样很方便,二是正态分布和非对称拉普拉斯分布的p.d.f. \text{p.d.f.}p.d.f.曲线比较相似。当采样点数量达到10万个是,结果是:
E Q [ X ] = 2.809685 , E Q [ X 2 ] = 13.770805 E_Q[X]=2.809685, \quad E_Q[X^2]= 13.770805EQ[X]=2.809685,EQ[X2]=13.770805
与真实值比较接近,但是没有均匀分布那个例子中的效果好(这一示例的R代码见文末“代码段C2”)。那是否换一个正态分布效果会好一点呢?这就引入一个新的问题,就是不同的分布Q QQ对重要性采样的结果有影响吗?
Part3:不同的分布Q QQ对结果有影响吗?
还以上面提到的两个例子来说明。
首先我们对X ∼ U ( 0 , 1 ) X \sim \text{U}(0,1)X∼U(0,1)选用不同的分布Q QQ,这些分布Q QQ的p.d.f. \text{p.d.f.}p.d.f.都具有如下形式:
q ( x ) = a x + 1 − 0.5 a , x ∈ [ 0 , 1 ] q(x)=ax+1-0.5a, \quad x \in [0,1]q(x)=ax+1−0.5a,x∈[0,1]
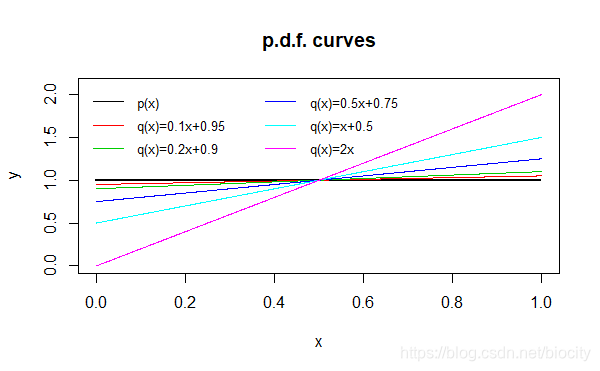
当a = 2 a=2a=2时,q ( x ) = 2 x q(x)=2xq(x)=2x就是上文中所使用的p.d.f. \text{p.d.f.}p.d.f.。我们对a aa取不同的值,就会得到不同的分布。这些不同的分布Q QQ的重要性采样结果如下: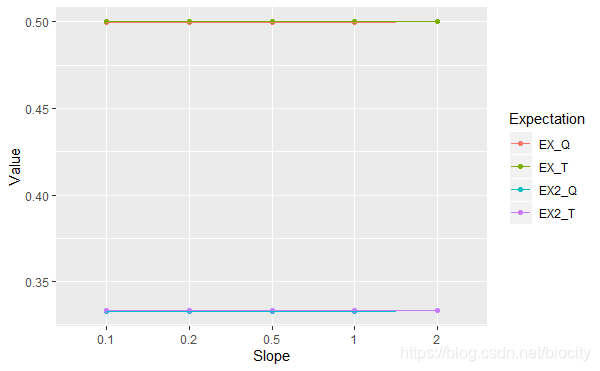
图中后缀T TT表示理论值,后缀Q QQ表示分布Q QQ重要性采样的结果。可以看出,不同的分布Q QQ的结果都很接近于理论值,并且彼此差异不大。
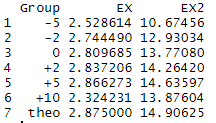
我们再看看X ∼ AL ( 1 , 0.5 , 0.2 ) X \sim \text{AL}(1,0.5,0.2)X∼AL(1,0.5,0.2)选用不同的分布Q QQ的结果
我们选用不同的正态分布作为分布Q QQ,这些正态分布的方差都一样,而均值以一定的位移(offset)分布在E T [ X ] E_T[X]ET[X]的左右两侧: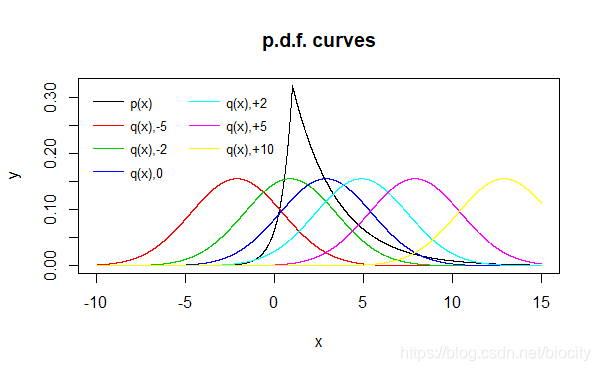
图例中“q(x)”后面的数字是正态分布的均值相对于E T [ X ] = 2.875 E_T[X]=2.875ET[X]=2.875的位移。我们取不同的位移,就会得到不同的分布。这些不同的分布Q QQ的重要性采样结果如下: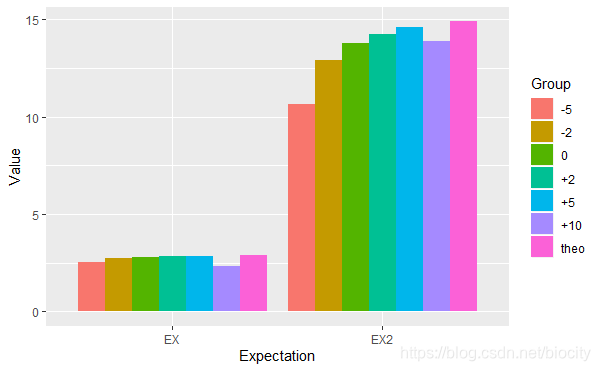
图中"theo"表示理论值。可以看出,不同的分布Q QQ的结果是有差异的,当位移是“+5”时最接近理论值。至于为什么一些分布的结果优于另一些分布,需要后续的学习研究。
(最后提一下,当然也可以通过调整方差来得到不同的正态分布,读者可自行验证。)
Part4:小结和附录代码
“重要性抽样”(Importance Sampling)的主要用途是通过采样计算数学期望,它不是一种用于直接采样的方法。我们列举了两个示例:均匀分布U ( 0 , 1 ) \text{U}(0,1)U(0,1)和非对称拉普拉斯分布AL ( μ , σ , p ) \text{AL}(\mu,\sigma,p)AL(μ,σ,p),通过选用对应的分布Q QQ采样后计算得到E [ X ] E[X]E[X]和E [ X 2 ] E[X^2]E[X2]的近似结果,验证了重要性采样的可行性。最后,我们讨论了采用不同的分布Q QQ可能对近似计算结果有影响,至于影响的原因(如何得到最优效果)有待后续学习研究。
参考
[1] “A Three-Parameter Asymmetric Laplace Distribution and Its Extension”, Keming Yu & Jin Zhang, 2006. Link https://doi.org/10.1080/03610920500199018
[2] “采样方法(一)”, CSDN. Link https://blog.csdn.net/Dark_Scope/article/details/70992266
最后给出文中用到的代码:
代码段C1
Unif <- function(a) {
b <- 1 - a / 2
Px <- function(x) 1
Qx <- function(x) a * x + b
ntry <- 100000
set.seed(123)
syQ0 <- runif(ntry, 0, 1)
syQ <- (sqrt(b ^ 2 + 2 * a * syQ0) - b) / a # sampling by q(x)
onetry <- function(x) Px(x) / Qx(x) * x
simuX <- sapply(syQ, onetry)
EX_Q <- mean(simuX) # simulative E(X)
onetry2 <- function(x) Px(x) / Qx(x) * x ^ 2
simuX2 <- sapply(syQ, onetry2)
EX2_Q <- mean(simuX2) # simulative E(X^2)
c(a=a, EX_Q=EX_Q, EX2_Q=EX2_Q)
}
format_formula <- function(a) {
b <- 1 - a / 2 # b >= 0 when a <= 2
prefix <- suffix <- ""
if (a == 0) {
return(paste0("q(x)=", b))
} else if (a == 1) {
if (b == 0) return("q(x)=x")
return(paste0("q(x)=x+", b))
} else {
if (b == 0) return(paste0("q(x)=", a, "x"))
return(paste0("q(x)=", a, "x+", b))
}
}
# test
test_a <- 2 # a is the slope and a <= 2.
Unif(test_a)
tmpx <- seq(0, 1, 0.001)
tmpy <- rep(1, length(tmpx))
npoint <- 1000
plot(tmpx, tmpy, col=1, xlab="x", ylab="y", main="p.d.f. curves", cex=.1,
ylim=c(0, test_a / 2 + 1.1))
curve(test_a * x + (1 - test_a / 2), 0, 1, n=npoint, add=T, col=2)
legend("topleft", legend=c("p(x)=1", format_formula(test_a)),
col=1:2, lty=1, bty="n", cex=.8, ncol=2)
# different values of a.
all_a <- c(0.1, 0.2, 0.5, 1, 2) # a is the slope and a <= 2.
res <- as.data.frame(t(sapply(all_a, Unif)))
# plot result of different values of a
res$EX_T <- 0.5 # theoretical E(X)
res$EX2_T <- 1 / 3 # theoretical E(X^2)
res$a <- factor(res$a, levels=res$a)
res
library(dplyr)
library(tidyr)
library(ggplot2)
res %>%
gather(Expectation, Value, -a) %>%
ggplot(aes(x=a, y=Value, color=Expectation, group=Expectation)) +
geom_point() +
geom_line() +
labs(x="Slope")
# plot p.d.f. curves
tmpx <- seq(0, 1, 0.001)
tmpy <- rep(1, length(tmpx))
npoint <- 1000
plot(tmpx, tmpy, col=1, xlab="x", ylab="y", main="p.d.f. curves", cex=.1,
ylim=c(0, max(all_a) / 2 + 1.1))
i <- 2
for (a in all_a) {
curve(a * x + (1 - a / 2), 0, 1, n=npoint, add=T, col=i)
i <- i + 1
}
legend("topleft", legend=c("p(x)", sapply(all_a, format_formula)),
col=1:(length(all_a) + 1), lty=1, bty="n", cex=.8, ncol=2)
代码段C2
# p.d.f. of the asymmetric Laplace distribution.
u <- 1
sg <- 0.5
p <- 0.2
ALx <- function(x, u, sg, p) {
if (x >= u) {
return(p * (1 - p) / sg * exp(-p * (x - u) / sg))
} else {
return(p * (1 - p) / sg * exp((1 - p) * (x - u) / sg))
}
}
Px <- function(x) ALx(x, u=u, sg=sg, p=p)
# theoretical value
EX_T <- C1 <- sg * (1 - 2 * p) / (p * (1 - p)) + u # theoretical E(X)
C2 <- sg / (p * (1 - p)) * sqrt((1 - 2 * p + 2 * p ^ 2))
EX2_T <- C2 ^ 2 + C1 ^ 2 # theoretical E(X^2)
# sampling/simulation parameters.
ntry <- 100000
# importance sampling
IS <- function(offset) {
Qx <- function(x) dnorm(x, C1 + offset, C2) # use normal distribution as q(x)
set.seed(123)
sy <- rnorm(ntry, C1 + offset, C2) # sampling by q(x)
onetryQ <- function(x) Px(x) / Qx(x) * x
simu_Q <- sapply(sy, onetryQ)
EX_Q <- mean(simu_Q) # simulative E(X) by importance sampling
onetryQ2 <- function(x) Px(x) / Qx(x) * x ^ 2
simu_Q2 <- sapply(sy, onetryQ2)
EX2_Q <- mean(simu_Q2) # simulative E(X^2) by importance sampling
c(Group=offset, EX=EX_Q, EX2=EX2_Q)
}
# test
test_offset <- 0 # offset from theoretical E(X)
IS(test_offset)
npoints <- 10000
xbegin <- -10
xend <- 15
plotPx <- function(x) sapply(x, Px)
curve(plotPx, xbegin, xend, n=npoints, col=1, xlab="x", ylab="y", main="p.d.f. curves")
Qx <- function(x) dnorm(x, C1, C2)
plotQx <- function(x) sapply(x, Qx)
curve(plotQx, xbegin, xend, n=npoints, add=T, col=2)
legend("topleft", legend=c("p(x)", "q(x)"),
col=1:2, lty=1, cex=.8, bty="n", ncol=2)
# different values of offset
all_offset <- c(-5, -2, 0, 2, 5, 10)
offset_labels <- c("-5", "-2", "0", "+2", "+5", "+10")
res <- as.data.frame(t(sapply(all_offset, IS)))
res$Group <- offset_labels
res <- rbind(res, c("theo", EX_T, EX2_T))
res$EX <- as.numeric(res$EX)
res$EX2 <- as.numeric(res$EX2)
res$Group <- factor(res$Group, levels=c(offset_labels, "theo"))
res
# plot the result of different values of offset.
library(dplyr)
library(tidyr)
library(ggplot2)
res %>%
gather(Expectation, Value, -Group) %>%
ggplot(aes(x=Expectation, y=Value, fill=Group)) +
geom_bar(stat="identity", position="dodge")
# plot the asymmetric Laplace distribution.
npoints <- 10000
xbegin <- -10
xend <- 15
plotPx <- function(x) sapply(x, Px)
curve(plotPx, xbegin, xend, n=npoints, col=1, xlab="x", ylab="y", main="p.d.f. curves")
i <- 2
for (offset in all_offset) {
Qx <- function(x) dnorm(x, C1 + offset, C2)
plotQx <- function(x) sapply(x, Qx)
curve(plotQx, xbegin, xend, n=npoints, add=T, col=i)
i <- i + 1
}
legend("topleft", legend=c("p(x)", paste0("q(x),", offset_labels)),
col=1:(i - 1), lty=1, cex=.8, bty="n", ncol=2, x.intersp=.5, text.width=2.5)