近世代数--循环群--怎么判断是不是循环群?
博主是初学近世代数(群环域),本意是想整理一些较难理解的定理、算法,加深记忆也方便日后查找;如果有错,欢迎指正。
我整理成一个系列:近世代数,方便检索。
个人感觉循环群需要原根的基础知识,这里是我对原根的部分记录。
三个方法:
- 1.定义
循环群:设群G GG中任意元素都可以表示成某一固定元素a aa的幂次,G = { a n ∣ n ∈ Z } , G=\{a^n|n\in Z\},G={an∣n∈Z},那么称G GG为循环群,a aa为群G GG的生成元,写成G = < a > G=<a>G=<a>。
- 2.循环群的子群也是循环群。
证明:假设循环群G = < a > , G=<a>,G=<a>,因为< e > <e><e>和< a > <a><a>不需要证明,直接是循环群,所以我们只需考虑那些非单位元{ e } \{e\}{e}、非群G GG本身的其他群,假设子群为H HH,
设s > 1 , s>1,s>1,是使得a s ∈ H a^s\in Has∈H的最小数,我们只需证H HH中的所有元素都可以用a s a^sas的幂次来表示即可。
我们假设a m a^mam是H HH的任意元素,那么m = q ⋅ s + r , ∃ q , r ∈ Z , 0 ≤ r < s m=q·s+r,{\exists}q,r\in Z,0\le r<sm=q⋅s+r,∃q,r∈Z,0≤r<s
我们有a r = a m ⋅ ( a − q s ) = a m ⋅ ( ( a s ) q ) − 1 a^r=a^m·(a^{-qs})=a^m·((a^s)^q)^{-1}ar=am⋅(a−qs)=am⋅((as)q)−1
因为a s ∈ H , a^s\in H,as∈H,由群的“封闭性”可知,( a s ) q ∈ H (a^s)^q\in H(as)q∈H;又由群的“单位元+逆元”可知,( ( a s ) q ) − 1 ∈ H ((a^s)^q)^{-1}\in H((as)q)−1∈H,所以a m ⋅ ( ( a s ) q ) − 1 ∈ H a^m·((a^s)^q)^{-1}\in Ham⋅((as)q)−1∈H,即a r ∈ H 。 a^r\in H。ar∈H。
又因为s ss是使得a s ∈ H a^s\in Has∈H的最小数,所以r = 0 r=0r=0,即m = q ⋅ s , a m = ( a s ) q m=q·s,a^m=(a^s)^qm=q⋅s,am=(as)q,即任意a m ∈ H a^m\in Ham∈H都可以写成a s a^sas的幂次形式。
- 3.素数阶群一定是循环群,非单位元都是生成元。
假设素数阶群为G GG,∣ G ∣ = p , p |G|=p,p∣G∣=p,p为素数。
任意元素a ∈ G , a ≠ e a\in G,a\neq ea∈G,a=e,由之前信息安全数学基础–群环域–拉格朗日定理(关于群的陪集)证过的∣ G ∣ = ∣ H ∣ ⋅ [ G : H ] |G|=|H|·[G:H]∣G∣=∣H∣⋅[G:H],我们知道任意子群∣ H ∣ |H|∣H∣与群∣ G ∣ |G|∣G∣的阶都是有整除关系的,即∣ H ∣ ∣ ∣ G ∣ |H|\mid |G|∣H∣∣∣G∣。根据群的“封闭性”,我们知道< a > <a><a>是G GG的子群,所以有∣ < a > ∣ ∣ ∣ G ∣ = p |<a>|\mid |G|=p∣<a>∣∣∣G∣=p。
此时,a ∣ G ∣ = 1 a^{|G|}=1a∣G∣=1。为什么不是≡ 1 ( m o d ∣ G ∣ ) \equiv 1(mod |G|)≡1(mod∣G∣),因为对于群( G , ⋅ ) (G,·)(G,⋅),运算⋅ ·⋅本身包含了⋅ ( m o d ∣ G ∣ ) ·(mod |G|)⋅(mod∣G∣)的意思,即每次做群运算都有⋅ ( m o d ∣ G ∣ ) ·(mod |G|)⋅(mod∣G∣),而不是最后乘法结果⋅ ( m o d ∣ G ∣ ) ·(mod |G|)⋅(mod∣G∣)。
又因为a ≠ e , → ∣ a ∣ ≠ 1 a\neq e,\rightarrow |a|\neq 1a=e,→∣a∣=1,所以∣ < a > ∣ = p |<a>|=p∣<a>∣=p,即G = < a > G=<a>G=<a>。
所以,非循环群最小阶数为4。
1阶群,只有一个元素,是循环群;
因为2、3是素数,所以2阶,3阶群是循环群;
- 唯一三阶群:{ 1 , a , b } \{1,a,b\}{1,a,b},循环群
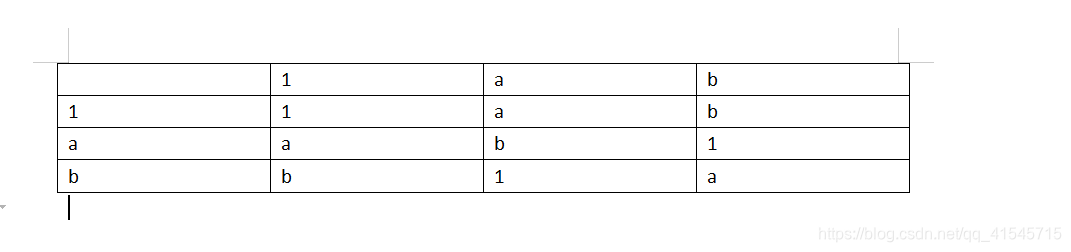
- 唯一三阶群:{ 1 , a , b } \{1,a,b\}{1,a,b},循环群
存在阶数为4的非循环群;
- 某个四阶群(四阶群不唯一):{ 1 , a , b , c } \{1,a,b,c\}{1,a,b,c},非循环群
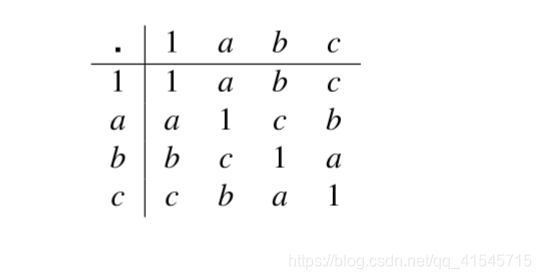
- 某个四阶群(四阶群不唯一):{ 1 , a , b , c } \{1,a,b,c\}{1,a,b,c},非循环群