public class SeqSearch {
    public static void main(String[] args) {
        int arr[] ={1,9,11,-1,34,89};
        int index = seqSearch(arr, -1);
        System.out.println(index);
    }

    public static int seqSearch(int[] arr,int value){
      for(int i=0;i< arr.length;i++){
          if(arr[i] == value){
              return i;
          }
      }
//    没找到
      return -1;
    }
}

二、二分查找

前提：在有序数组中

2.1 思路分析

下面的思路分析是基于数组是从小到大有序排序的时候（如果是从大到小，下面的第二步应该反过来）

首先确定该数组的中间的下标

mid = (left + right) / 2

然后让需要查找的数 findVal 和 arr[mid] 比较

findVal > arr[mid], 说明你要查找的数在mid 的右边, 因此需要递归的向右查找
findVal < arr[mid], 说明你要查找的数在mid 的左边, 因此需要递归的向左查找
findVal == arr[mid] 说明找到，就返回

什么时候我们需要结束递归

找到就结束递归

递归完整个数组，仍然没有找到findVal ，也需要结束递归当 left > right 就需要退出

2.2 代码实现（递归）

下面这种是普通方法实现

JavaSE——选择排序算法、冒泡排序法、二分查找法_我爱布朗熊的博客-CSDN博客

下面这种是使用递归实现

// 二分查找必须是有序的
public class BinarySearch {
    public static void main(String[] args) {
        int arr[] = {1,8,10,89,100,1234};
        System.out.println(binarySearch(arr,0,arr.length-1,1234));

    }
//  返回-1表示没有找到,找到了就返回下标
    public static int binarySearch(int[] arr,int left,int right,int findVal){


//      这种是没有找到的时候退出递归退出递归
        if(left>right){
            return -1;
        }

        int mid=(left+right)/2;
        int midVal = arr[mid];

        if(findVal >midVal){
//            大，找右边的
           return binarySearch(arr,mid+1,right,findVal);
        }else if(findVal <midVal){
//           小，向左
            return binarySearch(arr,left,mid-1,findVal);
        }else {
//          这是最终找到的时候退出递归
            return mid;
        }


    }

}

2.3 改善二分查找法——返回所有相同的数字下标

// 二分查找必须是有序的
public class BinarySearch {
    public static void main(String[] args) {
        int arr[] = {1,8,10,89,100,100,100,100,1234};
        System.out.println(binarySearch(arr,0,arr.length-1,100));

    }
//  返回-1表示没有找到,找到了就返回下标
    public static ArrayList<Integer> binarySearch(int[] arr, int left, int right, int findVal){


//      这种是没有找到的时候退出递归退出递归
        if(left>right){
            return new ArrayList<Integer>();
        }

        int mid=(left+right)/2;
        int midVal = arr[mid];

        if(findVal >midVal){
//            大，找右边的
           return binarySearch(arr,mid+1,right,findVal);
        }else if(findVal <midVal){
//           小，向左
            return binarySearch(arr,left,mid-1,findVal);
        }else {
//          这是最终找到的时候退出递归
            ArrayList<Integer> resIndexList = new ArrayList<>();
            int temp =mid-1;

//          因为我们这是二分查找法，所以我们最终找到的数的两边都有可能和这个数相等
            while (true){
                if(temp<0 || arr[temp] != findVal){
                    break;
                }
                resIndexList.add(temp);
                temp--;
            }
            resIndexList.add(mid);

//          再从中间向右
            temp = mid+1;
            while (true){
                if(temp> arr.length-1  || arr[temp] != findVal){
                    break;
                }
                resIndexList.add(temp);
                temp++;
            }
            return  resIndexList;

        }
    }
}

三、插值查找

插值查找算法类似于二分查找，不同的是插值查找每次从自适应mid处开始查找

对于数据量大，关键字分布比较均匀的查找表来说，采用插值查找，速度较快

关键字分布不均匀的情况下，该方法不一定比折半查找要好

3.1 思路分析

下面的公式一眼看上去很复杂，但是稍微一转变，很好记

(mid-left)/(right-left) = (findVal - arr[left])/(arr[right]-arr[left])

左边是下标，右边对应值

上面的公式，将左侧剩余mid，其余移动到右侧，便是下面的公式

3.2 代码实现

public class InsertValueSearch {
    public static void main(String[] args) {
        int[] arr = new int[100];

//      初始化数组
        for (int i = 0; i < 100; i++) {
            arr[i] = i + 1;
        }

        int search = insertValueSearch(arr, 0, arr.length - 1, 101);
        System.out.println(search);
    }

    /**
     * 前提：这个数组是有序的
     *
     * @param arr     传入的数组
     * @param left    左边的索引
     * @param right   右侧的索引
     * @param findVal 要查找的值
     * @return 最终查到的这个值的索引，如果没有找到就返回-1
     */
    public static int insertValueSearch(int[] arr, int left, int right, int findVal) {

//      退出的条件：
//        左侧的下标大于右侧的下标，不现实，肯定退出
        if (left > right || findVal < arr[left] || findVal > arr[right]) {
            return -1;
        }

//       求出mid
        int mid =left+(right-left)*(findVal-arr[left])/(arr[right]-arr[left]);
        int midVal = arr[mid];

        if(findVal>midVal){
//           说明向右侧递归查找
            return insertValueSearch(arr,mid+1,right,findVal);
        }else if(findVal<midVal){
            return insertValueSearch(arr,left,mid-1,findVal);
        }else

//     如果上面的两个if没有运行，则指定运行下面这个return
        return mid;
    }
}

四、斐波那契（黄金分割法）查找算法

参考下面两份资料

https://www.cnblogs.com/sha-Pao-Zi/p/16315064.htmlhttps://www.cnblogs.com/sha-Pao-Zi/p/16315064.html

36-查询算法-斐波那契查找3-分解1数组准备_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1ga411b7qF?p=37&spm_id_from=pageDriver&vd_source=c01240addcba226237f3c4781490fbae

黄金分割点是指把一条线段分割成两部分，使其中一部分与全长之比等于另一部分与这一部分之比。取其前三位数字的近似值是0.618.由于按此比例设计的造型十分美丽，因此称为黄金分割，也称中外比。

斐波那契数列{1,1,2,3,5,8,13,21,34,55}发现斐波那契数列的两个相邻数的比例，无限接近黄金分割值0.618，即将mid值设置成神器的黄金分割点(0.618)的位置

这个数列的后一个数是前两个数之和，如8=5+3

4.1 原理

与二分查找法、插值查找法相似，仅仅改变了中间节点(mid)的位置，mid不再是中间或插值得到，而是位于黄金分割点附近

即mid=low+F(k-1)-1,其中F代表斐波那契数列，low是数组最左侧元素的索引，k代表斐波那契数列的第几个元素

对F(k-1)-1的理解：

由斐波那契数列F[k] = F[k-1]+F[k-2]的性质，可以得到(F[k]-1)=(F[k-1]-1)+(F[k-2]-1)+1,该式说明：只要顺序表的长度为F[k]-1,则可以将该表分成长度为F[k-1]-1和F[k-2]-1的两段，即如图所示，从而中间位置为mid=low+F(k-1)-1

类似的，每一子段也可以用相同的方式分割
但顺序表长度n不一定刚好等于F[k]-1，所以需要将原来的顺序表长度n增加至F[k]-1。这里的k值只能使得F[k]-1恰好大于或等于n即可，由以下代码得到，顺序表长度增加后，新增的位置（从n+1到F[k]-1位置），都赋为n位置的值即可。

while(n>fib(k)-1)
   k++;

注意, 此时斐波那契数列是存放在数组中的, 所以会用F[]表示, 一定要注意跟F()的不同, 比如: F[6] =13 = F(7), F[0] = 1 = F(1)

4.2 难点解析图

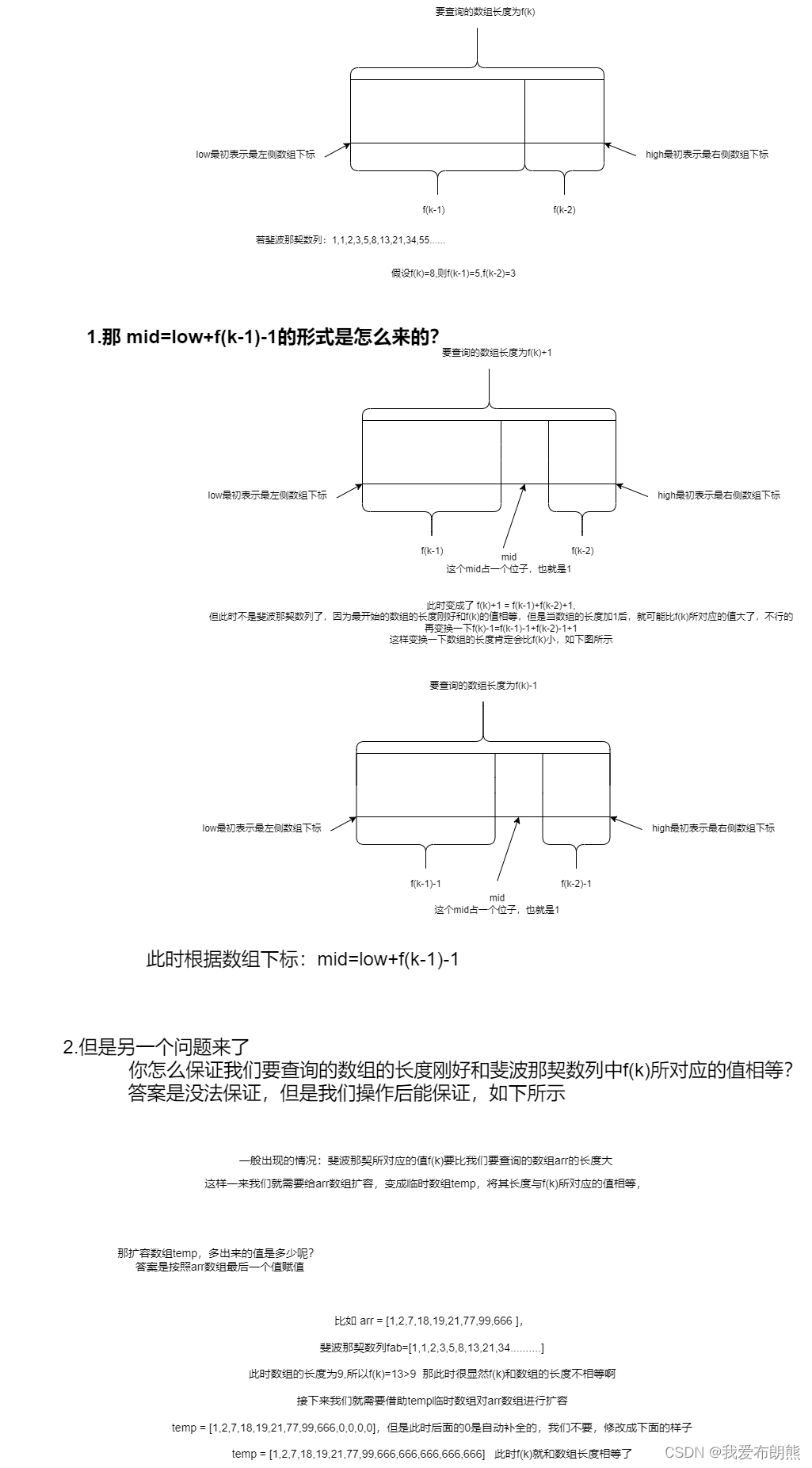
其实对于(F[k]-1)=(F[k-1]-1)+(F[k-2]-1)+1 及 mid=low+f(k-1)-1 还有另外一种理解方式，我不知道对不对，但是我感觉很有道理

最开始的数组的长度是f(k) = f(k-1)+f(k-2),此时代表的是长度，一定要注意

但是当我们获取下数组的时候就需要长度-1，数组的原因变成了 (F[k]-1)

然后我们把数组分成了三部分，左侧的部分的数组下标到f[k-1]-1,右侧到f[k-2]-1，但是此时我们中间还有一个mid，所示再+1（占一个下标的位子），故(F[k-1]-1)+(F[k-2]-1)+1

我觉得还是用上面的图理解更为合适，上面的图是从很多地方整理结合出来的，下面的文字是我自己想的有点不太对

4.3 代码

public class FibSearch {
    private static int maxSize = 20;

    public static void main(String[] args) {
        int[] arr = {1,8,10,89,1000,1234};
        System.out.println(fibSearch(arr,1234));

    }

    public static int[] fib() {
        int[] f = new int[maxSize];
        f[0] = 1;
        f[1] = 1;
        for (int i = 2; i < maxSize; i++) {
            f[i] = f[i - 1] + f[i - 2];
        }

        return f;
    }

    /**
     * @param a   数组
     * @param key 我们需要查找的关键码值
     * @return 返回对应的下标，如果没有-1
     */
    public static int fibSearch(int[] a, int key) {
        int low = 0;
        int high = a.length - 1;  //high下标对应的数据就是数组中最大的数
        int k = 0;  //表示斐波那契分割数值的下标
        int mid = 0;  //存放mid值
        int f[] = fib(); //获取斐波那契数列

//       获取到斐波那契分割数值的下标
//       为什么不写a.length()>f[k]? 而是两边同时-1成为high >f[k]-1 ？
//           应该也是可以的  这个的目的就是找出一个f[k]>=a.length的
        while (high > f[k] - 1) {
//           进入循环相当于没找到
            k++;
//            退出的条件  a.length()<=f[k]
        }

//      f[k]的值可能大于数组a的长度，因此我们需要使用Arrays类构造一个新的数组（临时数组）并指向a[]
//        if (f[k] > a.length) {  } 此时这里不用if语句判断f[k] > a.length，因为因为上面while的缘故f[k]>=a.length是一定的
//      将a数组拷贝到temp数组，并且temp数组的长度是f[k]的值，
        int[] temp = Arrays.copyOf(a, f[k]);
//       新扩充的地方用0补齐，但是我们需要用a数组的最后一位补齐，我们还得改一下temp数组
        for (int i = a.length; i < temp.length; i++) {
            temp[i] = a[a.length - 1];
        }

        while (low <= high) {
//           只要这个条件满足就一直找
            mid = low + f[k - 1] - 1;  //黄金分割点

            if (key < temp[mid]) {
//              向左找
                high = mid - 1;
//              为什么是k--？
//                  全部元素=f[k-1]+f[k-2]
//                  f[k] = f[k-1] + f[k-2]
//                  因为前面有f[k-1]个元素，这个f[k-1]依然可以再拆分
//                  带入公式变为f[k-1]=f[k-1-1]+f[k-1-2] 在前面的一部分找一个黄金分割点 高一知识
                k--;

            } else if (key > temp[mid]) {
//               向右
                low = mid + 1;
//              为什么是k=k-2?
//                全部元素=f[k-1]+f[k-2]
//                我们后面有k-2个元素，再对k-2进行拆分，把k-2个元素的部分想象成整个部分来看
//                f[k-2]=f[k-2-1]+f[k-2-2]  在后一部分找一个黄金分割点、满足斐波那契查找
//                最终就是下面的公式
                k = k - 2;
            } else {
//              找到了，但是需要判断返回的下标
                if (mid <= a.length-1) {
//                表示这个就是在原始的数组内找到的，并不是在扩容之后的内容
                   return mid;
                }else {
//                在扩容的内容里找到的
                    return a.length-1;
                }

            }
        }
//      整个while都没有返回表示没有找到对应的内容，则返回-1
        return -1;
    }

}

原文链接：https://blog.csdn.net/weixin_51351637/article/details/128443220