导读:在之前的博客中,我们已经粗略地讲了二阶前缀和和二阶差分,而且两种算法各给了一道类模板题,现在,我们再来讲一次二阶差分这个有点难理解的东西。
什么是二阶差分?简单而言,就是差分再差分。
在一些题目中,我们会对某个数组 a aa 进行一次差分,得到一个数组 s ss,其中 s ss 满足:s 1 = a 1 , s i = a i − a i − 1 ( i ≥ 2 ) s_1=a_1,s_{i}=a_{i}-a_{i-1}(i \geq 2)s1=a1,si=ai−ai−1(i≥2)。这个 s ss 数组就叫做 a aa 的差分数组。
现在,让我们再对 s ss 求一次差分,得到数组 s 2 s^2s2,其中 s 2 s^2s2 满足:s 1 2 = s 1 , s i 2 = s i − s i − 1 ( i ≥ 2 ) s_1^2=s_1,s_{i}^{2}=s_{i}-s_{i-1}(i \geq 2)s12=s1,si2=si−si−1(i≥2)。这个 s 2 s^2s2 就叫做 a aa 的二阶差分数组。
现在解决了定义的问题,那么作为一个数据结构,自然,最重要的应该是它能干什么。所以,二阶差分能干什么呢?
我们知道,对于部分区间问题,我们可以用一阶差分来高效地维护原数组,那么,类似地,二阶差分就是来高效的维护一阶差分数组的。
和一阶差分一样,二阶差分最难的一个部分就是它的修改部分,修改好后,剩下的事情就很简单了:做两次前缀和就得到了原数组。
如何维护二阶差分数组?因题而异。于是,我们来上一道模板题。
洛谷P4231 三步必杀 \color{green}{\texttt{洛谷P4231 三步必杀}}洛谷P4231 三步必杀
[Problem] \color{blue}{\texttt{[Problem]}}[Problem]
- n nn 个初始全部项为 0 00 的数列 a aa,m mm 次操作。
- 每次操作形如
l r s e,表示修改 a l ⋯ r a_{l \cdots r}al⋯r,修改的规则是,让 a l ⋯ r a_{l \cdots r}al⋯r 加上一个首项是 s ss 末项是 e ee 的等差数列。如执行1 3 1 5后,a 1 a_1a1 加 1 11,a 2 a_2a2 加 3 33,a 3 a_3a3 加 5 55。 - 最后输出 a aa 数组的异或和和最大值。
- 1 ≤ n ≤ 1 × 1 0 7 , 1 ≤ m ≤ 1 × 1 0 5 , 1 ≤ l < r ≤ n , 0 ≤ a i ≤ 9 × 1 0 18 1 \leq n \leq 1 \times 10^7,1 \leq m \leq 1 \times 10^5,1 \leq l < r \leq n,0 \leq a_i \leq 9 \times 10^{18}1≤n≤1×107,1≤m≤1×105,1≤l<r≤n,0≤ai≤9×1018。
[Solution] \color{blue}{\texttt{[Solution]}}[Solution]
看到区间加等差数列且查询原数组的次数不多,想都不用想,肯定是二阶差分。
上面说过了,二阶差分重点难点是如何修改(维护)二阶差分数组,这里推荐的一个做法是列表看看二阶差分数组每一项变化了些什么。
好,让我们来看看这个表格(d dd 表示公差):
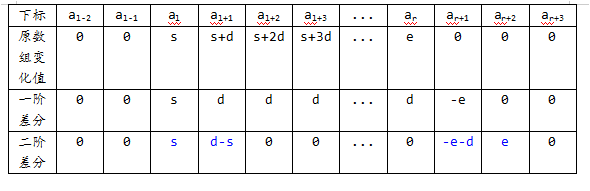
(Office 没有 Markdown,不好意思)
我们可以清楚地看到,我们只要修改蓝色的四个值就可以把二阶差分数组维护好了。这里就直接上代码啦。
[code] \color{blue}{\texttt{[code]}}[code]
const int N=1e7+100;
typedef long long ll;
ll s[N],ans,maxn;int n,m;
int main(){
n=read();m=read();
for(int i=1;i<=m;i++){
int l=read(),r=read();
ll b=read(),e=read(),d;
d=(e-b)/(r-l);//先要计算公差
s[l]+=b;s[l+1]+=d-b;s[r+1]-=e+d,s[r+2]+=e;
}//维护好二阶差分后的值
for(int i=1;i<=n+1;i++)
s[i]+=s[i-1];//一阶差分
for(int i=1;i<=n+1;i++)
s[i]+=s[i-1];//原数组
for(int i=1;i<=n;i++)
ans^=s[i],maxn=max(maxn,s[i]);
printf("%lld %lld",ans,maxn);
return 0;
}
当然,这里保证了 l < r l<rl<r,于是我们可以直接这样,但是当 l = r l=rl=r 时,我们需要一个特判(如何特判,留给读者思考啦)。
最后一提,做差分和前缀和的题目最好的思考方式就是想笔者一样列一个表格,多列几位,千万不要遗漏。