一、原理推导

最小二乘法 拟合平面是我们最常用的拟合平面的方法，但是有特殊的情况是用这种方法是不能拟合的，后续会加上这种拟合方法（RANSAC）。

matlab 最小二乘拟合平面（方法一） - 灰信网（软件开发博客聚合）

平面方程：Ax+By+Cz+D=0;

二、Matlab 实现

1、随机出来一些离散的点

>> clear
>> close all
>> % 随机生成一组（x,y,z）这些点的坐标离一个平面比较近
>> x0=1;L1=2;
>> y0=1;L2=2;
>> x=x0+rand(20,1)*L1;
>> y=y0+rand(20,1)*L2;
>> z=1+2*x+3*y;
>> scatter3(x,y,z,'filled')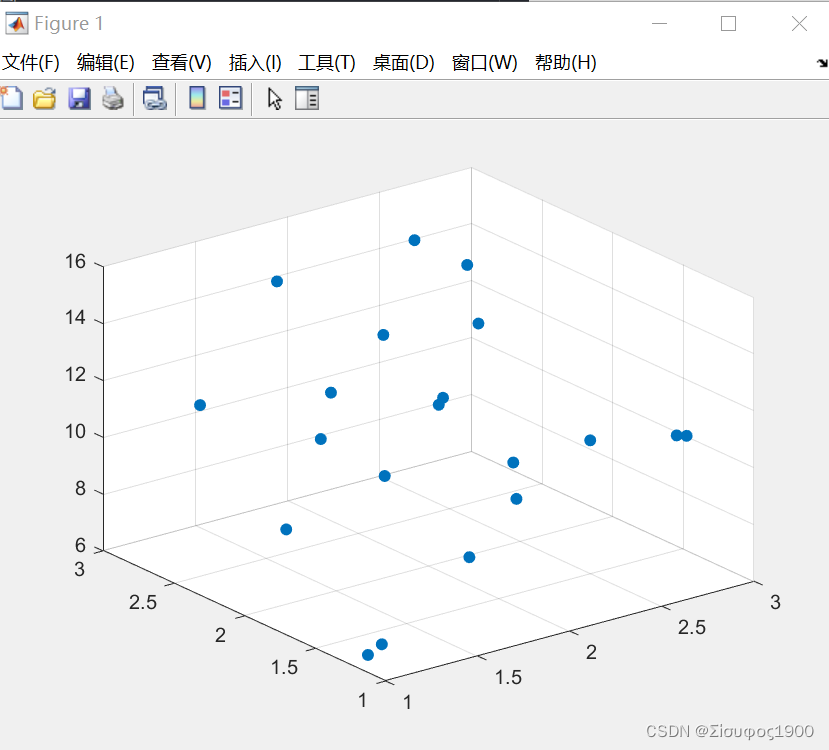

2、将其写成矩阵的形式：

x_a=sum(x)/length(data);% length(data)==20
y_a=sum(y)/length(data);
z_a=sum(z)/length(data);

% 平方的均值====================================================
xx_a=sum(x.*x)/length(data);
yy_a=sum(y.*y)/length(data);
zz_a=sum(z.*z)/length(data);

xy_a=sum(x.*y)/length(data);
xz_a=sum(x.*z)/length(data);
yz_a=sum(y.*z)/length(data);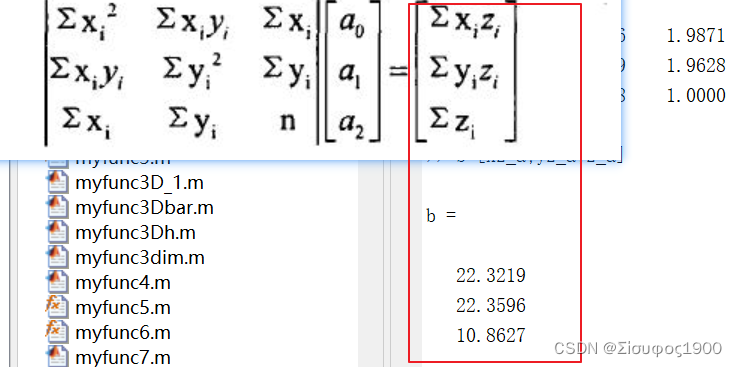

 3、求出a0  a1 a2也就是 -A/C   -B/C   -D/C

b=[xz_a;yz_a;z_a];

XYZ=A^-1 *b;  % 方程求系数
a0=XYZ(1); % -A/C
a1=XYZ(2); % -B/C
a2=XYZ(3); % -D/C

4、求平面法向量

V=[a0 a1  -1];% 平面法向量
nor=norm(V); % 向量的模
normalize_V=[a0/nor  a2/nor  -1/nor]; % 平面法向量归一化

5、 开始绘制图像

scatter3(x,y,z,'filled')
hold on;
xfit=min(x):0.1:max(x);  % 坐标系的坐标
yfit=min(y):0.1:max(y);
[XF,YF]=meshgrid(xfit,yfit);% 生产XY点列 

ZF=a0*XF+a1*YF+a2;  %计算Z的值

% 显示
mesh(XF,YF,ZF)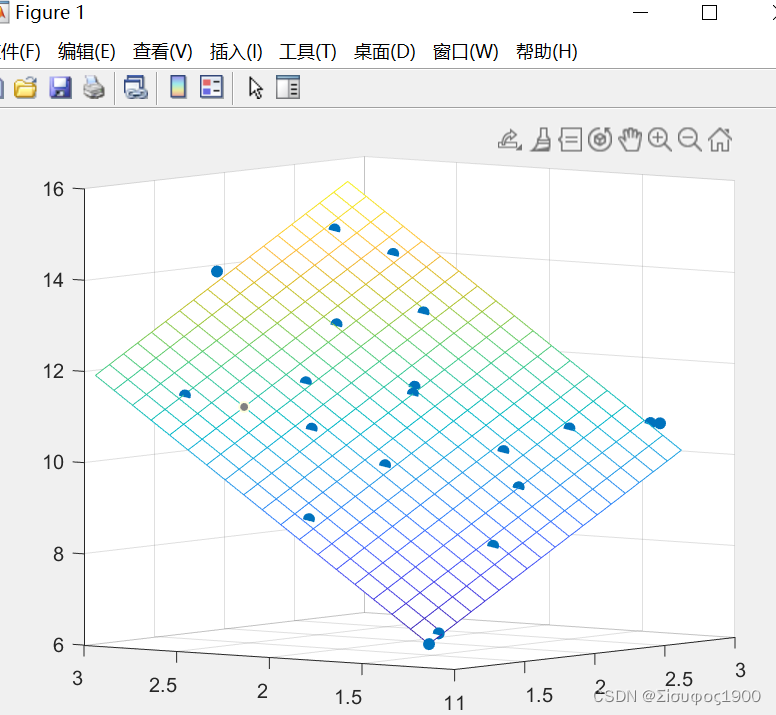

clear
close all
% 随机生成一组（x,y,z）这些点的坐标离一个平面比较近
x0=1;L1=2;
y0=1;L2=2;
x=x0+rand(20,1)*L1;
y=y0+rand(20,1)*L2;
z=1+2*x+3*y;
scatter3(x,y,z,'filled')
hold on;
data=[x,y,z];
x=data(:,1);
y=data(:,2);
z=data(:,3);
x_a=sum(x)/length(data);% length(data)==20
y_a=sum(y)/length(data);
z_a=sum(z)/length(data);

% 平方的均值====================================================
xx_a=sum(x.*x)/length(data);
yy_a=sum(y.*y)/length(data);
zz_a=sum(z.*z)/length(data);

xy_a=sum(x.*y)/length(data);
xz_a=sum(x.*z)/length(data);
yz_a=sum(y.*z)/length(data);


% 方程组的系数矩阵
A=[xx_a  xy_a  x_a;
   xy_a  yy_a  y_a;
   x_a   y_a    1];

b=[xz_a;yz_a;z_a];

XYZ=A^-1 *b;  % 方程求系数
a0=XYZ(1); % -A/C
a1=XYZ(2); % -B/C
a2=XYZ(3); % -D/C

V=[a0 a1  -1];% 平面法向量
nor=norm(V); % 向量的模
normalize_V=[a0/nor  a2/nor  -1/nor]; % 平面法向量归一化


% 开始绘制图像
scatter3(x,y,z,'filled')
hold on;
xfit=min(x):0.1:max(x);  % 坐标系的坐标
yfit=min(y):0.1:max(y);
[XF,YF]=meshgrid(xfit,yfit);% 生产XY点列 

ZF=a0*XF+a1*YF+a2;  %计算Z的值

% 显示
mesh(XF,YF,ZF)

三维点集拟合：平面拟合、RANSAC、ICP算法_wishchin的博客-CSDN博客_三维曲面拟合算法