洛谷CF1111D

题目传送门

这是竞赛生涯中切的第一道黑题！！！千万别降紫了啊

题面translate：
给一个字符串，由至多52种字符组成，m次询问，每次询问两个字符x和y，问有多少种重排方案使得所有同种字符在前一半或者后一半，并且x和y必须在同一半。
n,m≤10^5​ 且为偶数。
思路：
首先统计每种字符的出现次数，记为 t_i。先不考虑x和y，对于一种合法方案，需要选出一个子集使得其和为n/2，每种选法对应的排列方案数是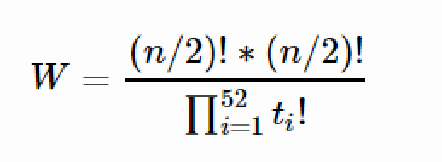

因为 n/2个元素全排列就 (n/2)! 种可能性，但其中有一些相同的类型 比如说 1,1 这两个1，一个出现在3位置，一个出现在5位置,反过来一个，出现在5位置，一个出现在3位置 ，这两种情况 其实是一样的，所以要除以他们 相同元素间的阶乘，就好啦！同样，剩下的几个元素 组合出来的情况就是 (n/2)! /{ 剩下元素出现次数的阶乘 的乘积 }，结合在一起的话，那满足B条件下的组合方式 的数量就是

(n/2)! *(n/2)! / (所有元素出现次数的阶乘的乘积) = W (恒定的)

注意： 在模运算中 除一个数 我们要 转变为成一个数的逆元，因为1e9+7是质数，所以用费马小定理求逆元就行咯！
于是我们就可以先预处理出w，以便后面使用！
然后我们考虑x，y这个条件，设考虑x，y这个条件后，方案数是d，那么根据乘法原理，总的答案就是

2 * w*d（乘2是因为把n分成了两半）

那么我们怎么求d呢？
其实就是k件物品，填满容量为n/2的背包的方式，这里呢套个01背包计数就好了！
问题又来了，x,y这两个类型的物品，要放在一起，怎么解决呢？
因为询问次数有点大，不能暴力排除x,y的背包 转化一下的话，其实我们可以预处理先求出完整k件物品的背包，让x,y挪出去，其实是对应的把 x,y的背包贡献减去即可 这里可以预处理下，对付很大的x,y询问(要注意观察数据范围额)
AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
ll dp[100010],bp[100010],a[60][60],v[100010],inv[100010],fac[100010],W;
char s[100010];
int get_pos(char c) 
{
	if (c>='A'&&c<='Z') return c-'A'+1;
	else return c-'a'+1+26;
}
ll quickpow(ll a,ll n) 
{
	ll res=1;
	while(n>0) 
	{
		if(n&1) res=res*a%mod;
		a=a*a%mod;
		n>>=1;
	}
	return res;
}

void get_w(int n) 
{
	fac[0]=1;
	int m=n/2;
	for(int i=1;i<=n;i++) fac[i]=i*fac[i-1]%mod;
	W=fac[m]*fac[m]%mod;
	for(int i=1;i<=52;i++) //费马小定理求逆元
	{
		if(v[i]==0) continue;
		inv[i]=quickpow(fac[v[i]],mod-2);
		W=W*inv[i]%mod;
	}
}
void init() 
{
	scanf("%s",s+1);
	int len=strlen(s+1);
	for(int i=1;i<=len;i++) v[get_pos(s[i])]++;
	get_w(len);
	dp[0] = 1;
	int m=len/2;
	for(int i=1;i<=52;i++) 
	{
		if(v[i]==0) continue;
		for(int j=m;j>=v[i];j--) dp[j]=(dp[j]+dp[j-v[i]])%mod;
	}
	for(int i=1;i<=52;i++) 
	{
		if(v[i]==0) continue;
		for(int j=1;j<=52;j++) 
		{
			if(v[j]==0) continue;
			for(int k=0;k<=m;k++) bp[k]=dp[k];//背包中去掉i物品
			for (int k=v[i]; k<=m;k++) bp[k]=(bp[k]-bp[k-v[i]]+mod)%mod;//这里+mod的原因是减完可能为负，所以+mod使之为正
			if(i!=j) for(int k=v[j]; k<=m;k++) bp[k]=(bp[k]-bp[k-v[j]]+mod)%mod;
			a[i][j]=bp[m];
		}
	}
}
int main() 
{
	init();
	int q;
	scanf("%d",&q);
	while(q--) 
	{
		int x,y;
		scanf("%d%d",&x,&y);
		int px=get_pos(s[x]),py=get_pos(s[y]);
		printf("%lld\n",a[px][py]*W*2%mod);
	}
	return 0;
}