1、meshgrid函数
在利用MATLAB进行3D图形绘制时,往往需要一些采样点,然后根据采样点进行图形绘制。meshgrid函数是用于生成网格采样点的函数,示例如下:
x=-3:1:3;
y=-2:1:2;
[X,Y]=meshgrid(x,y)
运行结果:
运行结果如图所示,这里meshgrid(x,y)的作用是分别产生以向量x为行,向量y为列的两个大小相同的矩阵。
2、quiver函数
quiver函数是MATLAB中使用箭头绘制二维矢量场的函数,使用该函数可以绘制矢量函数,基本格式为:quiver(x,y,u,v,scale) 该调用格式表示通过(x,y)指定的位置绘制小箭头来表示以该点为起点的向量(u,v),通过处处绘制箭头就得到了二维的矢量场,二维矩阵x,y,u,v具有一一对应的关系。scale表示箭头长度是否伸缩,等于0.5为缩短一半;等于2为长度扩大1倍;等于1则不做伸缩。示例如下
x = [0 0 0 0];
y = x;
u = [1 -1 0 0];
v = [0 0 1 -1];
quiver(x, y, u, v);
该程序是绘制4个矢量,起点均为(0,0),分别指向(1,0)、(-1,0)、(0,1)、(0,-1)。运行结果: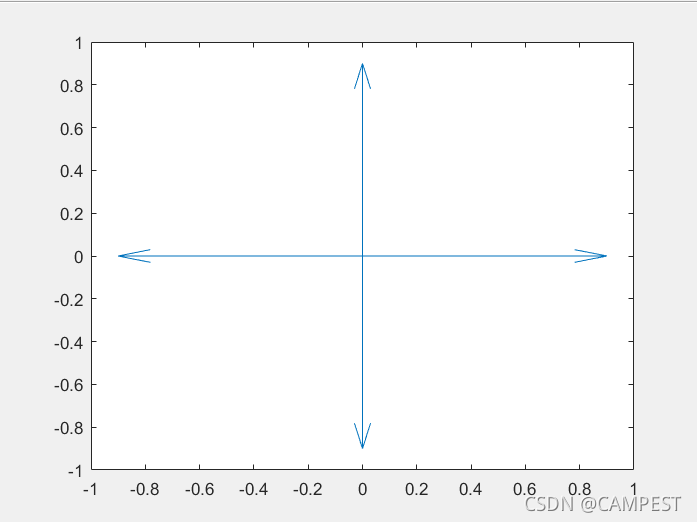
可以看到并未完全指到对应的点,需要加入scale参数,将其设为1后结果如下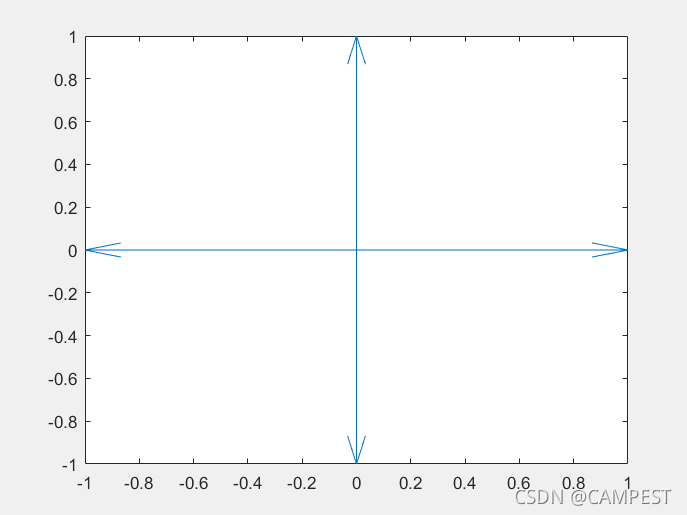
另有一种调用格式quiver(u,v),作用是在xoy面上绘制向量(u,v),由于没有指定向量的起点,所以在平面上均匀的取若干个格点作为起点。
u = [1 1 1; 1 1 1];
v = u;
quiver(u, v);
结果如下: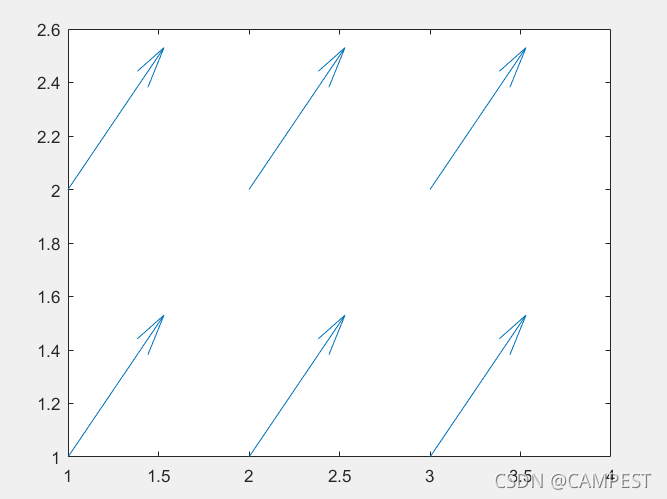
3、streamline函数
streamline函数是从二维或三维矢量数据中绘制流线的函数,两种使用基本格式如下:
(1)、streamline(x,y,u,v,startx,starty)
基于二维向量数据u,v绘制流线,定义矢量u,v的位置坐标x,y必须是单调的,但不需要间隔均匀,且x和y有相同数量的元素,startx和starty定义流线的起始位置。
(2)、streamline(x,y,z,u,v,w,startx,starty,startz)
该函数基于三维数据u,v,w绘制流线,示例如下
[x,y] = meshgrid(0:0.1:1,0:0.1:1);
u = x;
v = -y;
figure
quiver(x,y,u,v) %绘制箭头图
startx = 0.1:0.1:1;
starty = ones(size(startx)); %定义起点坐标
streamline(x,y,u,v,startx,starty) %绘制流线图
运行结果: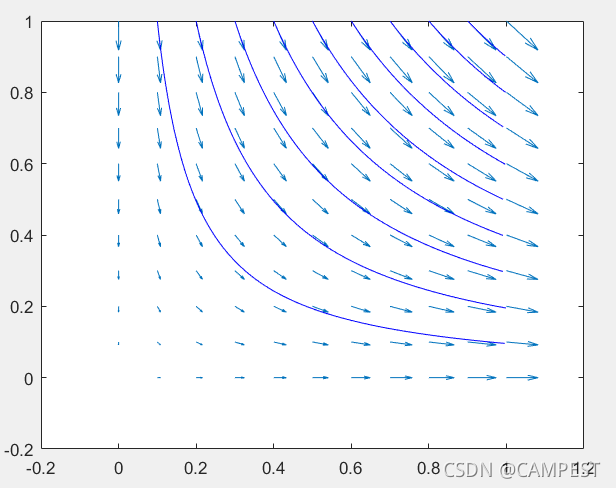
4、矢量函数实例讲解
基于以上所介绍的相关函数,可以利用这些函数实现矢量函数的图形绘制。
(1)u = y ∗ c o s ( x ) , v = y ∗ s i n ( x ) u=y*cos(x),v=y*sin(x)u=y∗cos(x),v=y∗sin(x)图形
[x,y] = meshgrid(0:0.2:2,0:0.2:2); %生成所需的网格采样点,x与y在0到2区间,每隔
%0.2取一个点,这样就在0到2中产生100个采样点
u = cos(x).*y; %定义u分量
v = sin(x).*y; %定义v分量
quiver(x,y,u,v) % 绘制二维矢量场图
这段代码直接给出矢量函数的两个分量,然后用箭头绘制出来,绘制结果如下: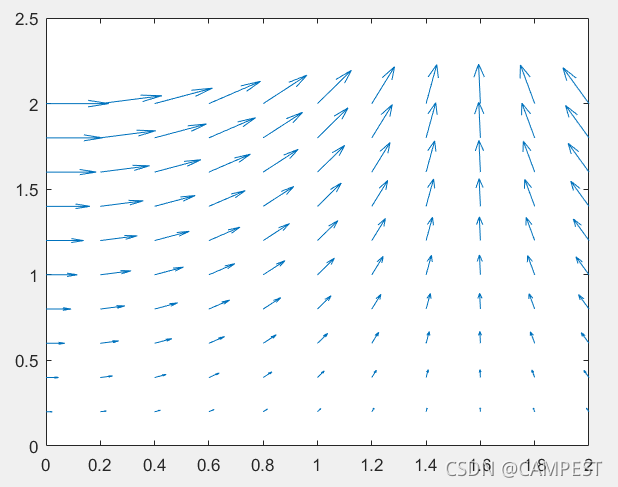
(2)u = c o s ( x + 2 ∗ y ) , v = s i n ( x − 2 ∗ y ) u=cos(x+2*y),v=sin(x-2*y)u=cos(x+2∗y),v=sin(x−2∗y)图形
syms x y real %定义符号变量x、y
F = [ cos(x+2*y), sin(x-2*y) ]; %定义矢量函数
[X,Y]=meshgrid(-2:.25:2); %生成网格
Fxf = inline(vectorize(F(1)),'x','y'); %使用内联函数inline构造函数Fxf
Fyf = inline(vectorize(F(2)),'x','y'); %使用内联函数inline构造函数Fyf
Fx = Fxf(X,Y); %计算网格数据对应的Fx的值
Fy = Fyf(X,Y); %计算网格数据对应的Fy的值
quiver(X,Y,Fx,Fy,'k') %画出二维矢量场
axis tight; %坐标轴范围与数据范围一致,紧凑模式
set(gca,'position',[0 0 1 1]) %去掉图像白边
这段代码使用了符号变量定义函数,将其离散化后绘制矢量图。结果如下: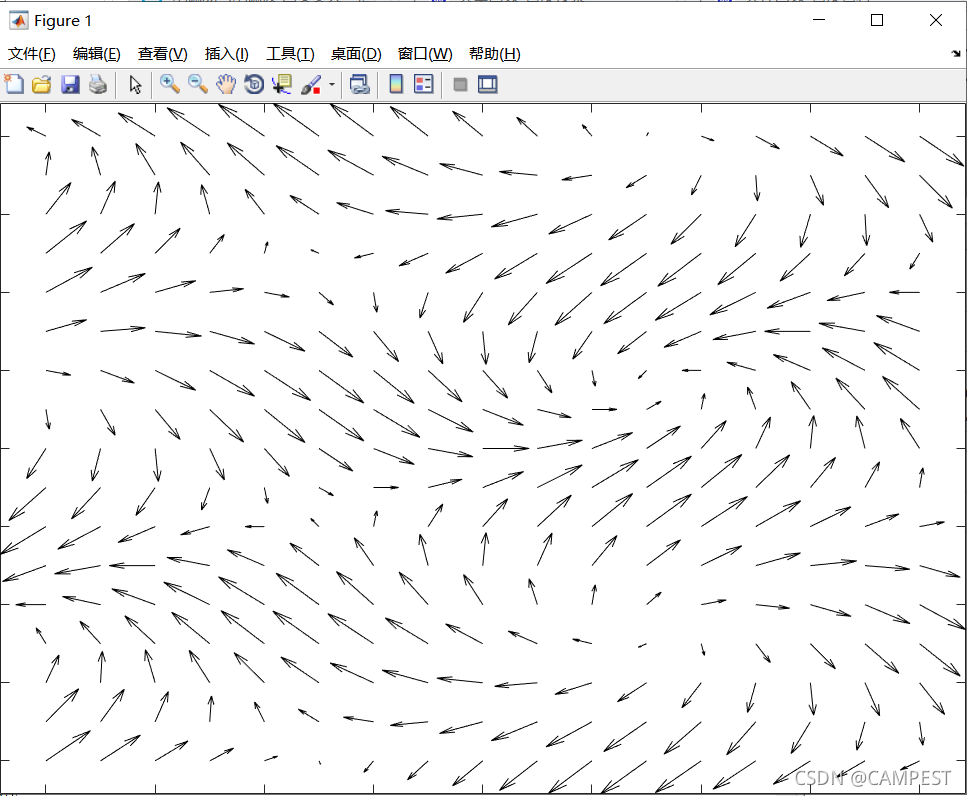
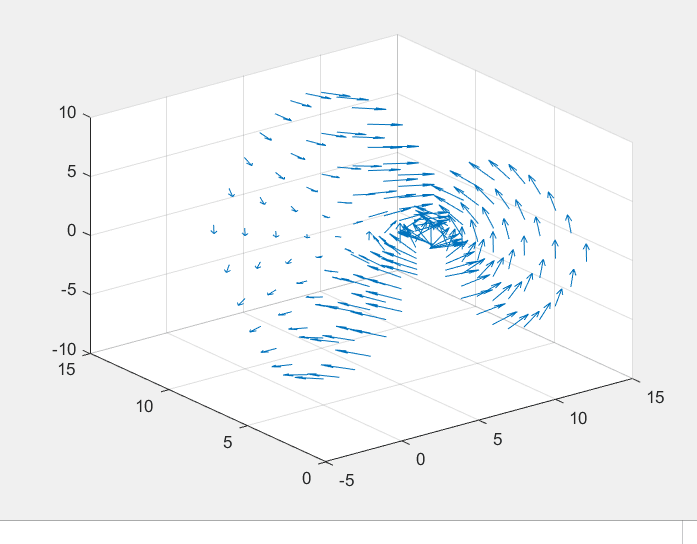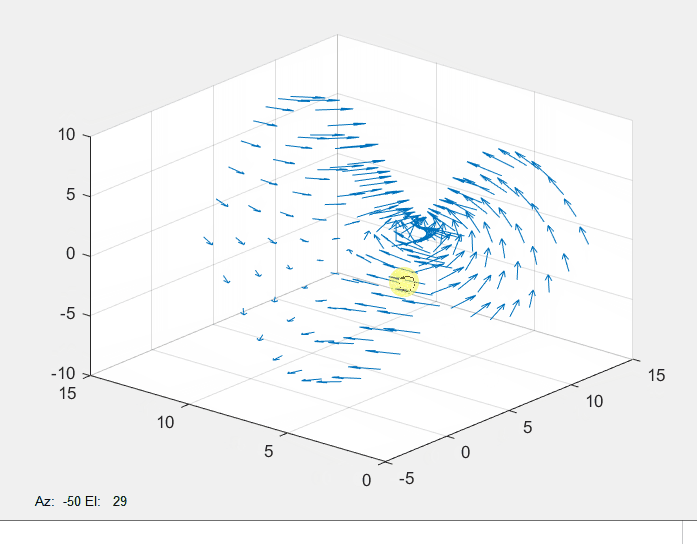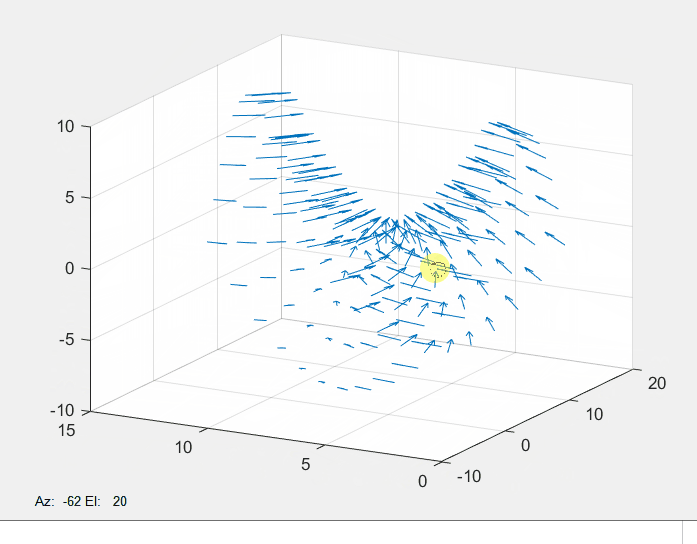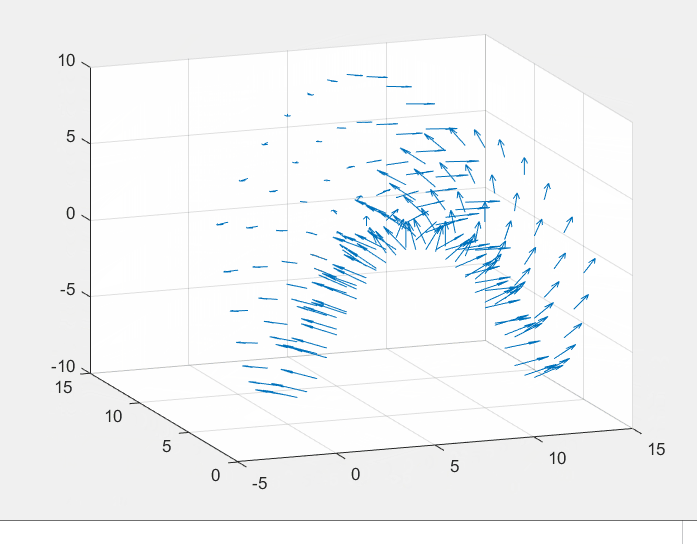
(3)z = y 2 − x 2 z=y^2-x^2z=y2−x2三维图形
quiver3函数与quiver函数类似,可以绘制三维的矢量场图,代码如下:
[x,y]=meshgrid(-3:.5:3,-3:.5:3); %生成所需的网格采样点,x与y在-3到3区间
z=y.^2-x.^2; %定义函数
[u,v,w]=surfnorm(z) %取三维曲面的法线
quiver3(z,u,v,w) %绘制三维矢量场图
结果如下: