目录
参考资料来自B站“猴博士爱讲课系列”这里
一. 概率论部分
随机事件和概率
1.古典概型



2.几何概型

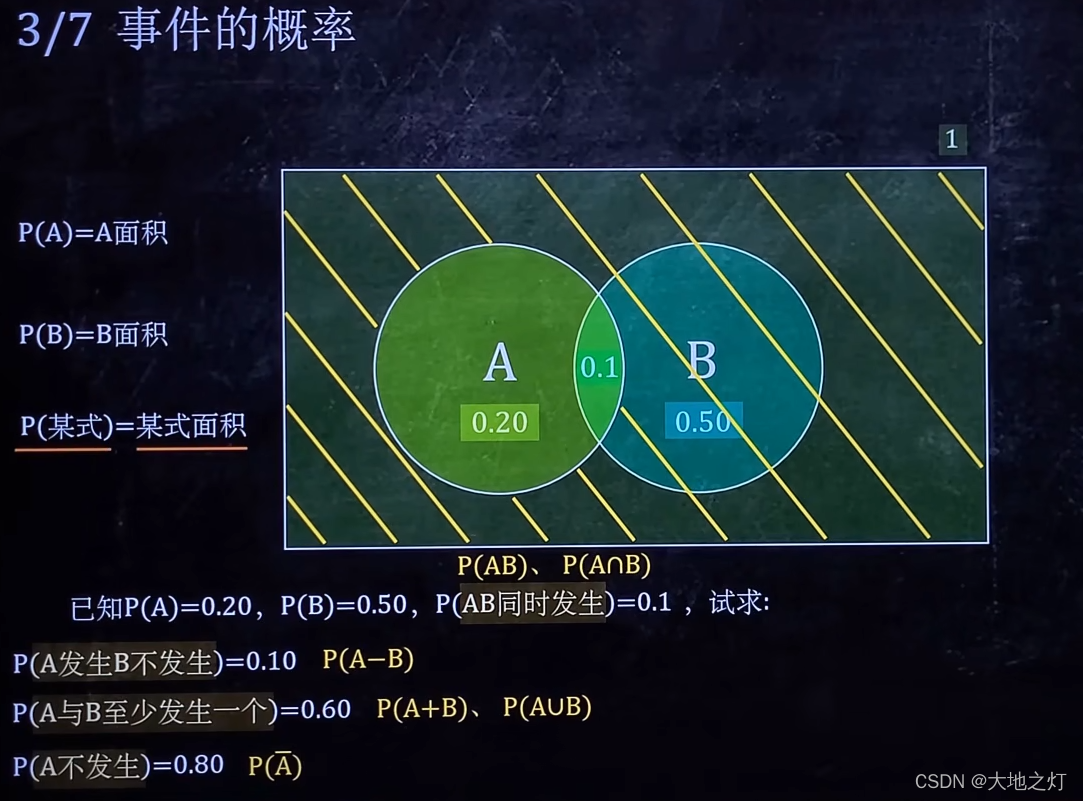
3.事件的概率
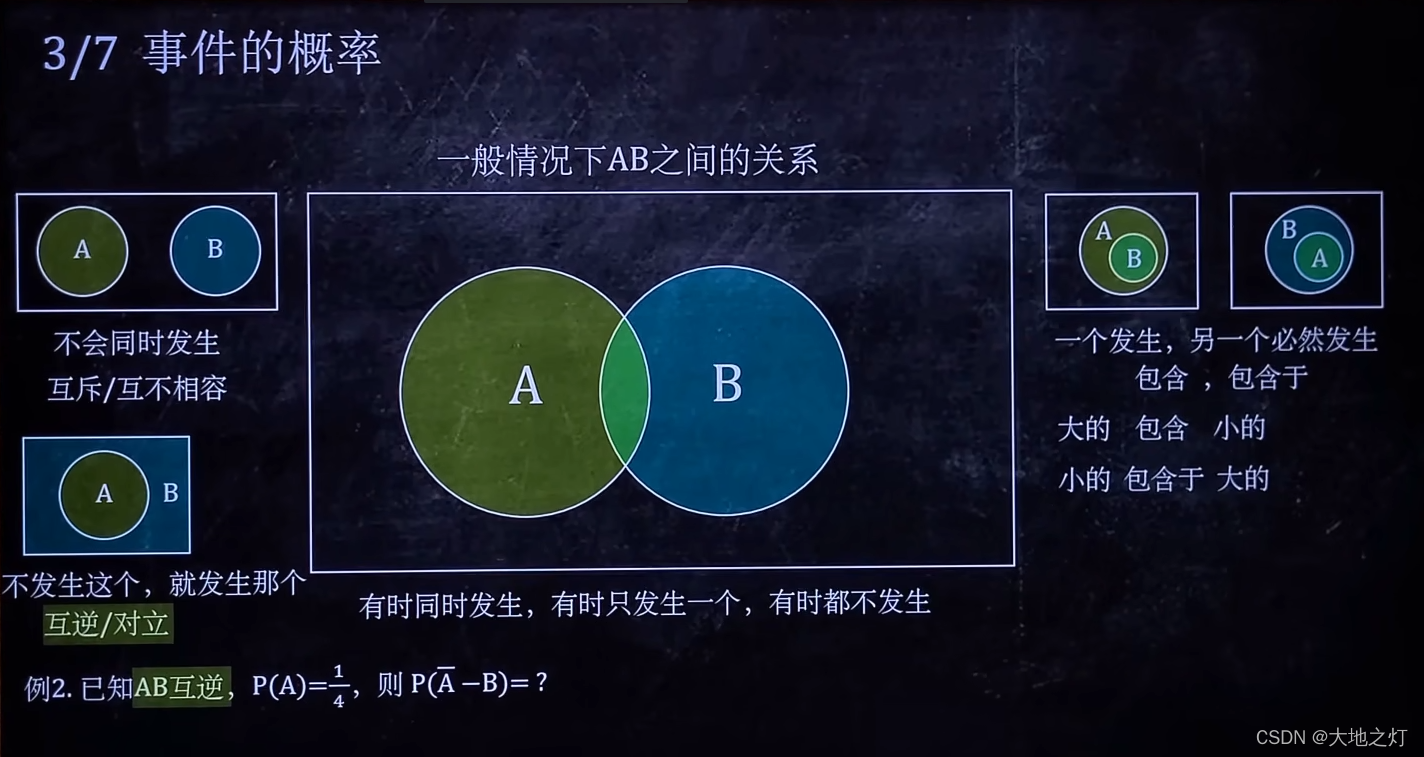
4.事件的独立性

5.条件概率

6.全概率公式


7.贝叶斯公式


二. 数理统计部分
| 连续与离散
离散型
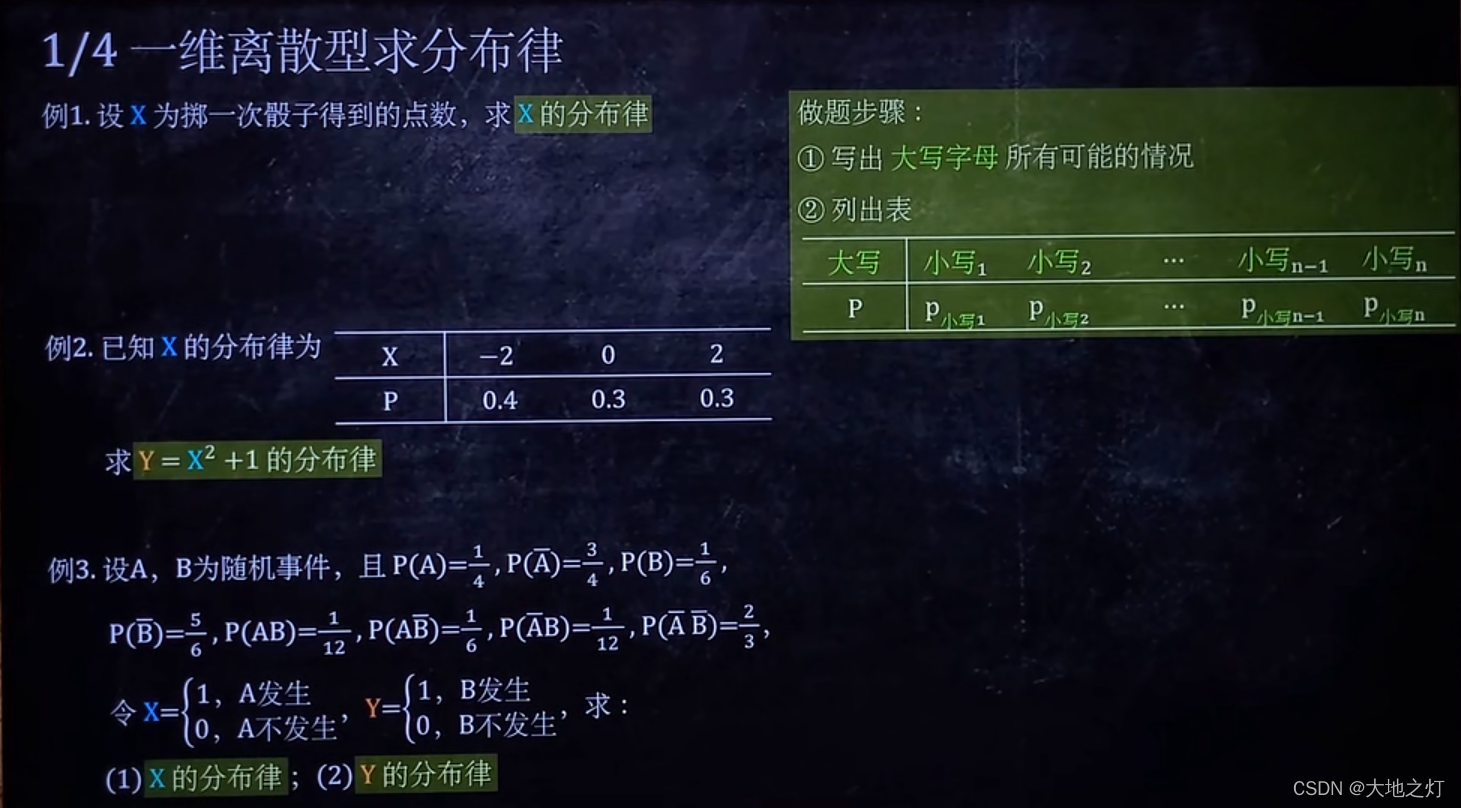
1.一维离散型求分布律

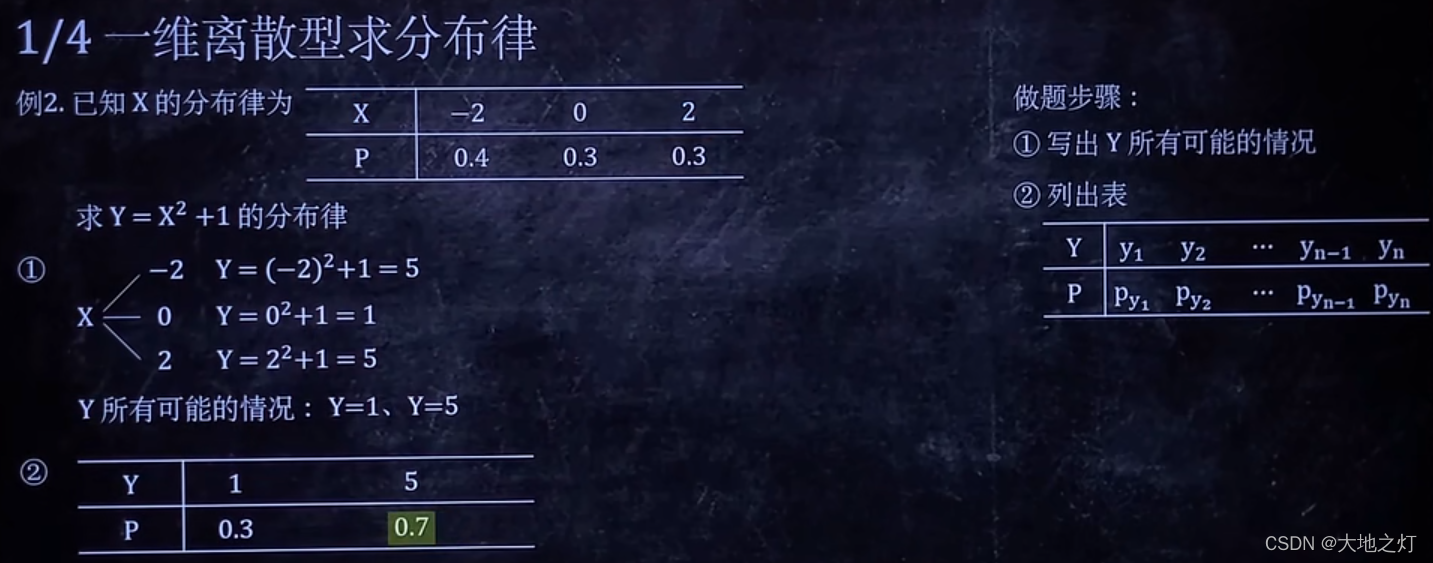
**注意:**分布律的另外一种写法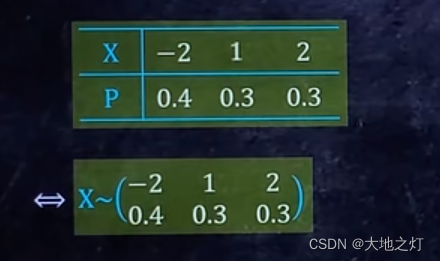
2.一维离散型求期望,方差
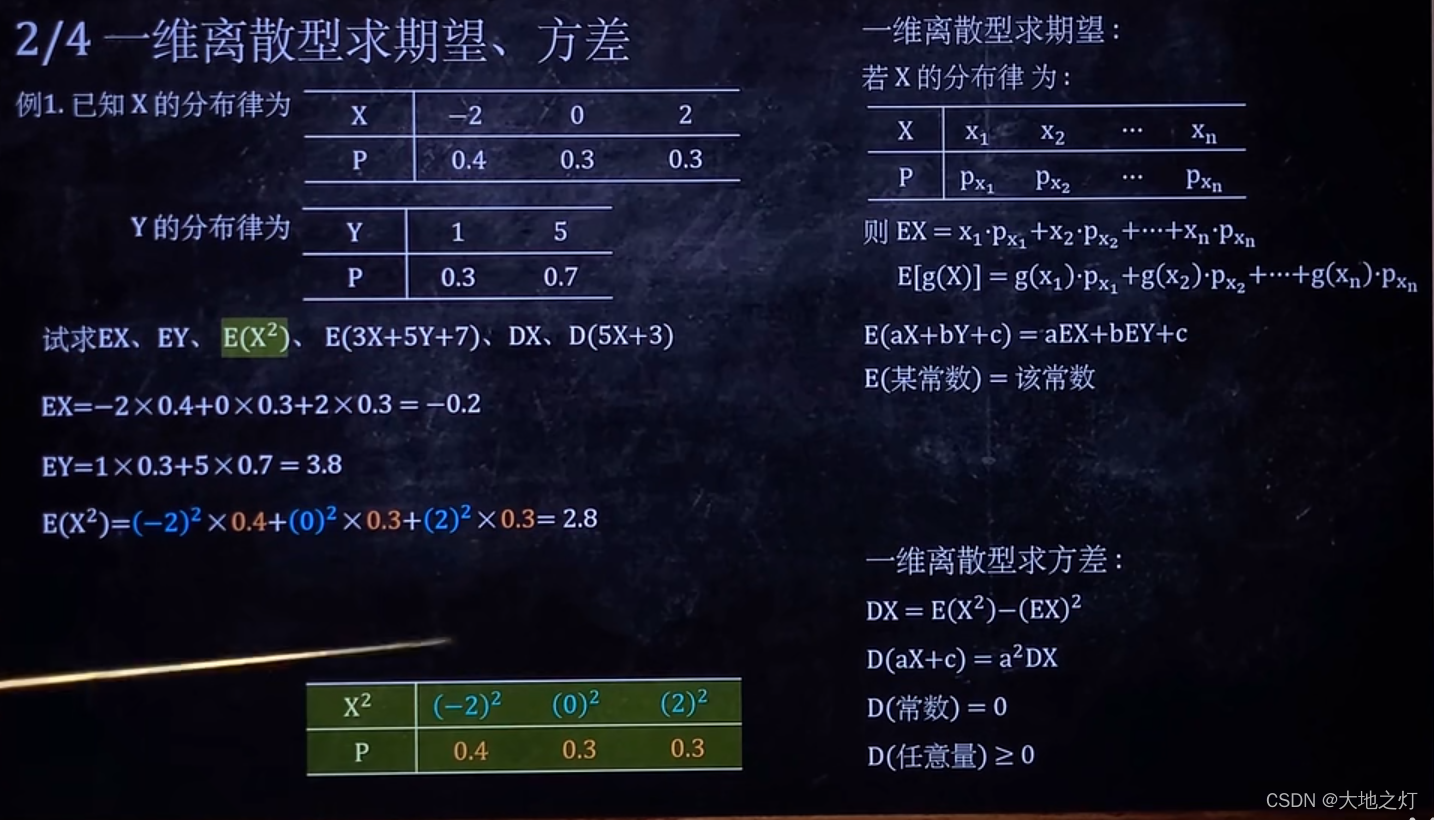
注意: 上面求 E ( X 2 ) E(X^2)E(X2) 的平方的时候,绿色的图示严格来讲并不是 X 2 X^2X2 的期望,因为 ( − 2 ) 2 (-2)^2(−2)2 和 ( 2 ) 2 (2)^2(2)2 其实是一种情况,应该要合并一下。不过题目只是要求计算结果,所以不会有什么影响。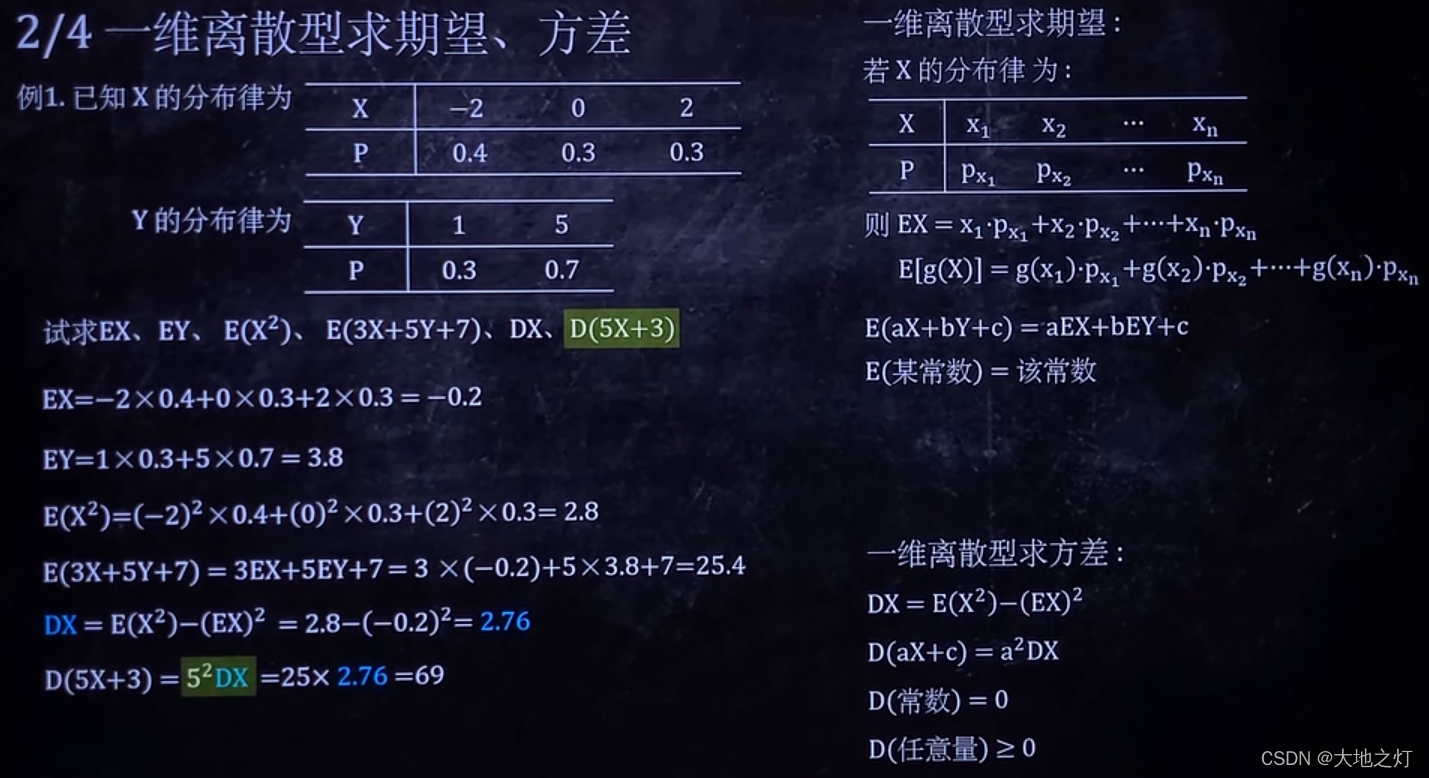
3.二维离散型求分布律

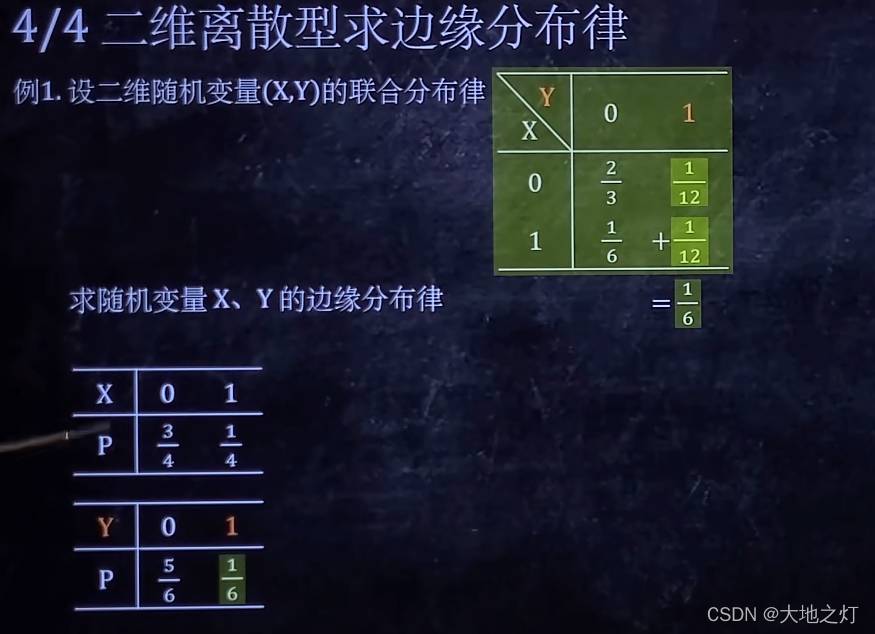
4.二维离散型求边缘分布律
连续型
一维连续型随机变量
题目一:

注意:
对概率密度从− ∞ − + ∞ -∞ -+∞−∞−+∞的积分为1
未知数只有M MM时,f M ( m ) f_M(m)fM(m)可以简写成f ( m ) f(m)f(m)
一维连续型求F
表示成对应概率再求解

一维连续型已知 F 求 f
f A ( a ) = F A ′ ( a ) f_A(a)=F^{'}_A(a)fA(a)=FA′(a)
一维连续型求F

普通法:所有题目都能用

公式法:
条件:若在f X ( x ) ≠ 0 f_X(x)\neq0fX(x)=0的区间内,Y = g ( X ) Y=g(X)Y=g(X)是单调递增或者单调递减
第一步 & 第二步

第三步:
第四步:

一维连续型求期望,方差
求E ( X ) E(X)E(X)
求E ( X 2 ) E(X^2)E(X2)
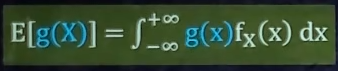
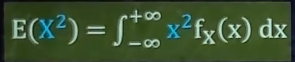

求D ( X ) D(X)D(X)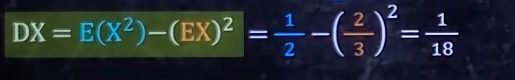
版权声明:本文为qq_33489955原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。