1. 基本概念

• 算法：解决问题的方法或过程； （性质：输入、输出、确定、有限)
• 程序：算法用某种程序设计语言的具体实现 （可不满足有限性）
  例如：操作系统，它是无限循环中执行的程序。

2. 课前准备

• 图结构的存储结构代码实现；
• DFS算法的代码实现；
• 快速排序算法的代码实现；

void QuickSort(SqList &L)
{ QSort(L,1,length); } //QuickSort
//对顺序表L进行快速排序

void QSort(SqList &L, int low, int high)
{ if(low<high)
   { pivotloc=Partition(L,low,high);
     QSort(L,low,pivotic-1);
     QSort(L,pivotloc+1,high);
   }
 }//QSort  

• 折半查找算法的代码实现。

3. 计算机解题的四大思维

顺序、循环、分支、递归

4.例题（伪代码写法）

① 试编写求1+2+……+n的总和

ALGORITHM   N_SUM(n)
//INPUT:正整数n
//OUTPUT: 1+2+……+n的总和sum
     sum ←0;
     for i=1 to n do
        sum←sum+i;
      OUTPUT sum;

② 在n个不同的数中找最大的数。

ALGORITHM FindMax(array L(n), MAX)
  //Input：数组L的下标 i =1,2,3,……n
  //Output：L中的最大项MAX
  MAX←L(1); i←2;
  while i≤=n do
    if  MAX<L(i) then MAX←L(i); 
    i←i+1;
  Output MAX;

比较操作进行n-1次，故：T(n)=O(n)

③ 将数组A的数从小到大排序

ALGORITHM SelectionSort(A[0..n-1])
//input: n个数据的数组A
//output: 从小到大排好序的数组A
for i ← 0 to n–2 do
	min ← i;
	for j ← i + 1 to n–1 do
		if A[j] < A[min] then min ← j;
	swap A[i] and A[min];

T(n)=O(n²)

④ Add array A[m, n] and B[m, n] as C[m, n]

ALGORITHM ADD(A, B)
//input: array A[m, n] and B[m, n]
//output: array C[m, n]
     for i=1 to m                   ------m+1 times 
         for j=1 to n                ------m*(n+1) times
              C[i, j]←A[i, j]+B[i, j]; ------ m*n times

O(m*n) ≤O(n²) //suppose m≤n

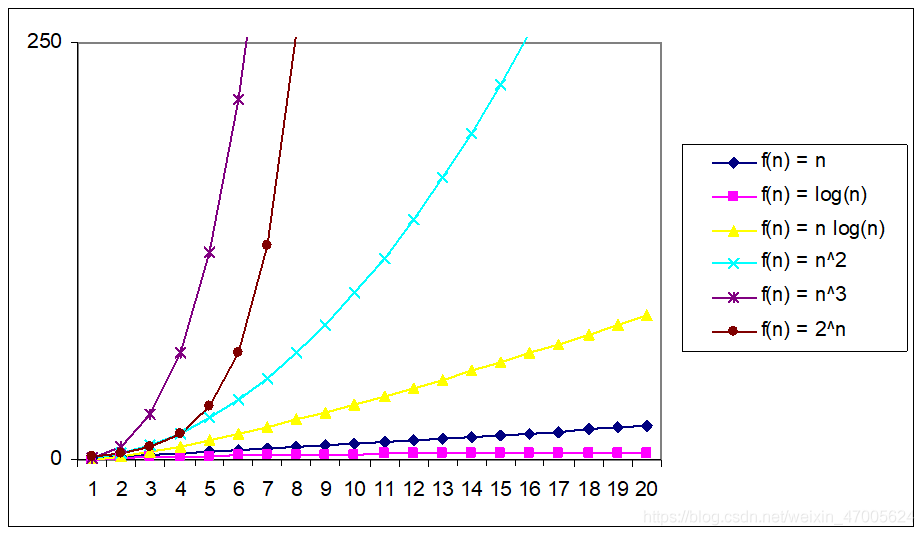
5. 常见T(n)的快慢比较图

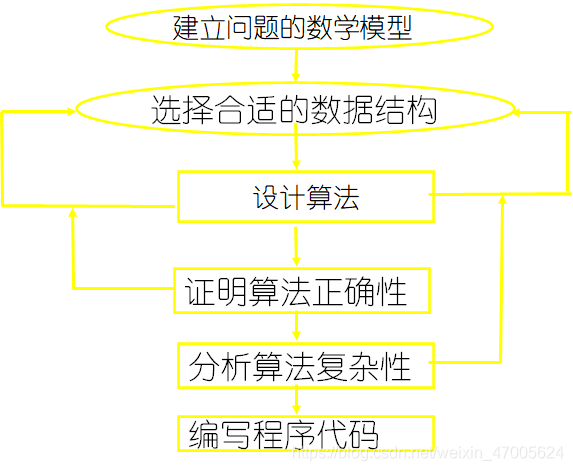
6. 问题求解的基本过程