决策树三大算法ID3、C4.5和CART

所有公式内容来自小象学院的邹博老师

一、决策树
决策树是一种树形结构，每一个内部节点表示在某一属性上的测试，每一条分支代表一个测试输出，每一个叶子节点代表一种类别。
决策树采用的是自顶向下的递归方法，其基本思想是以信息熵为度量建立一个信息熵下降最快的树。到叶子节点处的熵值为0，每一个叶子节点中的实例都属于同一类。
需要解决的问题：当前节点应该选择哪个属性来划分。
ID3、C4.5和CART就是用来解决上述问题并建立一棵决策树。

二、ID3算法原理及步骤

1、信息熵
信息熵是对一个事件包含的信息量的期望，该事件包含的信息量跟它可能的结果有关，可以这样认为信息熵 = (结果1发生时的信息量 + … + 结果n发生时的信息量)。
假设一个事件x结果为1的概率为0.9，为0的概率为0.1。那结果0和结果1都包含了信息，那谁的信息量大呢，显然是结果0，因为它是概率小，如果它发生了那可能有很多不可思议的信息，结果1的概率为0.9，它发生接近必然事件，没有什么信息可言。事件每个结果的发生概率直接决定了这个结果的信息量，而且信息量的大小跟概率是倒数的关系，你小我大，你大我小，因为概率在0和1之间，所以log(概率)表示信息量最合适了，记得加个负号哦。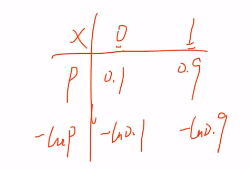
在这里插入图片描述
现在我们来求事件x的信息熵记为H(x):
假设事件x有k种结果，p_i表示每种结果的发生概率。则
H(x):

乘以p_i 相当于加权，因为所有的p_i相加等于1。根据公式可知当p_i服从均匀分布时信息熵最大，此时所有结果发生概率都为1/k，结果难以预料，所以信息熵可以用来描述一个事件的不确定性。

2、条件熵
上面我们求出了独立事件X的信息熵的公式，现在我们来求事件X和事件Y的联合事件的信息熵H(X,Y)：

H(X,Y)=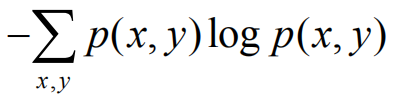
在这里插入图片描述
其中，小x和小y分别表示事件X和事件Y个某个结果，(x, y)是X结果和Y结果的笛卡儿积。
联合事件的信息熵减去独立事件的信息熵记为条件熵，H(Y|X)表示的是在X事件发生的前提下事件Y发生带来的信息熵，推导如下：
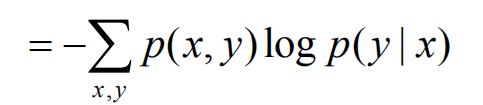
在这里插入图片描述

因为H(Y|X)表示的是在X事件发生的前提下事件Y发生带来的信息熵，所以上式拆分必须先固定x在固定y。(上式有两种拆法，x前y后或者y前x后，具体情况具体分析)

上式小写x表示的是事件X的某种结果。

条件熵公式：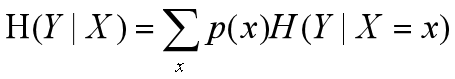
在这里插入图片描述
3、信息增益

信息增益：
我们知道H(Y|X)表示的是在X事件发生的前提下事件Y发生的信息熵(不确定性)，H(Y)表示事件Y独立发生的信息熵(不确定性)。那么H(Y)-H(Y|X)表示的就是在X事件发生的前提下事件Y的不确定性减少的程度，这就是X对于Y的信息增益。信息增益越大，事件Y的不确定性就越小，它的结果就可以预料。

下面我们从数据集的(分类)角度来探讨信息增益：
假设现在想要把一个数据集D分成K个类，数据集中的数据具有多个特征。那么我们应该选择哪个特征来划分呢？答案是求每个特征的信息增益，选最大的那一个特征。

数据集D的熵：
数据集D划分为K个类，那么这K个类就是数据集D的K个结果，每个类的概率用 该类的样本数/总样本数 来求。对于一个即将对它进行分类的数据集来说，它的熵意味着它的纯度(它可以被分为K个类则纯度最低，它只能被分为一个类则纯度最高)。
在这里插入图片描述
其中：
|C_k| / |D|表示的是第K个结果出现的概率。

信息增益的计算：
基本的记号如下：
在这里插入图片描述
用g(D,A)表示特征A对于数据集D的信息增益，计算如下：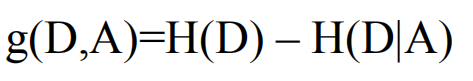

数据集D就像事件Y，对D用K个类来划分就像是事件Y有K个结果，D_k个就是K个结果中的某一个。
特征A就像事件X，特征A的n个取值就像事件X的n个结果，A_i就是n个结果中的某一个。
在这里插入图片描述

P(A_i)表示的是特征A(有n个取值)的取第i个值的概率，用数据集D中在特征A的第i个取值上相同的样本数（就是D_i）比上数据集D的总样本数来求。这里可以举个例子，假设有一个西瓜数据集D，瓜纹是西瓜数据集D的其中一个特征，瓜纹这个特征就有多个取值，比如条纹、全黑、全绿等等，这里P(A_i)指的就是瓜纹特征的不同取值的概率，用西瓜数据集D中瓜纹为该取值的样本数比上西瓜数据集D的总样本数来求。

p(D_k|A_i)表示的是以特征A取第i个值为前提的第k个类的概率。特征A取第i个值得到数据集D_i，用数据集D_i中属于第k个类的样本数（就是D_ik）比上数据集D_i的总样本数得到p(D_k|A_i)。

小结一下：
依据特征A的n个不同取值我们可以把数据集D分为n个数据集D_i，1=<i<=n。从条件熵H(D|A)的最终公式可以看出，H(D|A)等于这n个数据集自身的熵乘上它所依据的特征A的取值的概率再相加。如果H(D|A)的值比较小，意味着根据A特征划分数据集后大部分的样本已经属于同一个类，因为 g(D,A) = H(D) - H(D|A)，所以g(D, A)会比较大。
对于其他的特征我们都可以求其对于数据集D的信息增益，选择信息增益最大的那个特征来划分数据集D，我们会得到一个最纯的划分结果，划分后的数据集中的样本基本属于同一个类。

ID3算法建立决策树的步骤：

1、计算当前数据集的经验熵。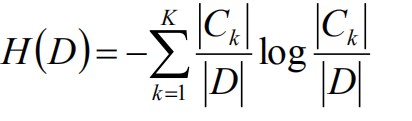
在这里插入图片描述
2、遍历所有特征求每个特征的信息增益。

3、选择信息增益最大的特征划分当前数据集。对于当前数据集所划分的所有子集，如果某个子集出现下面情况则迭代结束。情况如下：
(1)当前集合中的样本属于同一个类，无需划分。
(2)当前集合中的样本在所有属性上取值相同(虽然它们属于不同的类)，无法划分。
(3)当前集合为空，不能划分。
4、对于能划分的所有子集，重复1、2、3步骤。

例：ID3决策树及可视化

# -*- coding: utf-8 -*-
# 使用ID3算法预测销量高低
import pandas as pd
import numpy as np
# 参数初始化
path = 'F:/DataMining/chapter5/sales_data.xls'
# 规定第一列是索引列，这样就不会再默认生成新的索引列
data = pd.read_excel(path, index_col='序号')  # 导入数据
print('data: \n', data)
# 因为数据是中文，所以要进行数值化处理(Numerical processing)
# 用1来表示'好'，'是','高'这三个属性，用-1来表示'坏','否','低'
data[data == '好'] = 1
data[data == '是'] = 1
data[data == '高'] = 1
data[data != 1] = -1
print('data_np: \n', data)
# 将dataframe格式转换为矩阵格式
# x = data.iloc[:, :3].as_matrix().astype(int)
# y = data.iloc[:, 3].as_matrix().astype(int)
# 或者将dataframe格式转换为数组格式
x = np.array(data.iloc[:, :3]).astype(int)
y = np.array(data.iloc[:, 3]).astype(int)
from sklearn.tree import DecisionTreeClassifier as DTC
# criterion用来选择一个衡量一次划分的标准，可以取gini或者entropy(熵)
dtc = DTC(criterion='entropy')
dtc.fit(x, y)

# 导入相关函数，可视化决策树
# 导出的结果是一个dot文件，需要安装Graphviz才能将它转换为pdf或者png等格式
from sklearn.tree import export_graphviz
# 获取列名列表
x = data.iloc[:, :3].columns.values.tolist()
print('x:\n', x)
with open("tree.dot", 'w') as f:
    export_graphviz(dtc, feature_names=x, out_file=f)

三、C4.5算法

思考这样一个问题：如果我们用数据集D的编号这一特征来划分它，假设有m个样本，那数据集D会被划分为m个子数据集，每个子数据集中只有一个样本，这些子数据集已经很纯了。这种情况我们算得的编号特征信息增益肯定是最大的，但是基于这个特征建立的模型显然不具备泛化能力。

显然信息增益对于特征取值比较多的特征有所偏好，为了减少这种偏好带来的影响，C4.5算法不直接使用信息增益，而使用信息增益率。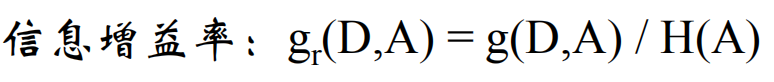
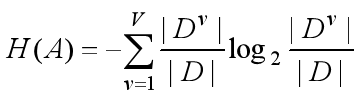
在这里插入图片描述
其中v=1代表A的第一个取值，V代表A的总共取值个数。
对于我们提出的问题，C4.5可以很好的解决。编号特征的信息增益大，但是它的信息熵同样非常大。但是C4.5却对特征取值比较少的特征有所偏好。因此C4.5规定不直接选择增益率最大的特征，而是先选择信息增益超过平均水平的特征，再从这些特征中选择信息增益率最大的特征。

四、CART算法
数据集D的不纯度用基尼值来度量：

在这里插入图片描述
Gini(D)表示的是从数据集D中随机抽取两个样本，其类别标记不一致的概率。因此Gini(D)越小，则数据集D的纯度越高。

特征A的基尼指数定义为：
D_i表示的根据特征A的n个特征所划分的n个数据集。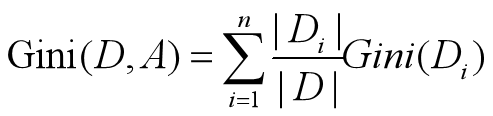
在这里插入图片描述
最终选择Gini指数最小的特征为最优划分特征。

五、决策树的评价
在这里插入图片描述
六、防止决策树过拟合

为了防止决策树过拟合，可以采用剪枝和随机森林的方法来改善。
这里介绍剪枝的方法：
预剪枝
思路：在生成决策树的时候就判断它的节点需要不要剪枝。
步骤：
从根节点开始，统计出根节点中哪个类别的样本数最多，用该类别标记根节点，此时根节点还没有划分，我们记为决策树T₀。然后用测试集对目前的决策树T₀(只有一个根节点)进行测试求测试集精度，也就是用T₀来划分测试集，它的测试精度等于 正确划分的测试样本数 / 测试集的总样本数。
接着计算根节点的最优划分属性，用最优划分属性把根节点划分，对于划分后的各个叶子节点，用同样方法给它们标记一个类别(哪个类别样本数多就标记为哪一类)，这就得到新决策树T₁。这时再用测试集来求 T₁ 的测试精度，如果该节点划分之后的决策树T₁的测试集精度等于或者小于没有划分的决策树T₀的测试集精度，那我们就不划分这个节点。如果划分之后测试集精度明显提升，那就根据最优属性划分这个节点，对于划分之后的各个叶子节点，通过同样的方法来判断它到底要不要划分。(没有划分，就相当于剪枝了)
缺点与优点：很多节点都没有展开(都被剪枝),显著减少训练时间和测试时间。但是会导致欠拟合。

后剪枝
1、思路
决策树创建完成之后再判断需要剪枝的内部节点。
在这里插入图片描述
2、确定剪枝系数
纠正：对以r为根的树剪枝，剪枝后只保留r本身而删掉它的所有子树。

3、剪枝算法
剪枝系数选择最小：由α=0和α=无穷大这两种情况来看，等于0代表不用剪枝，等于无穷大意味着我们要剪的只剩单根节点才能保证损失最小，所以α越小代表剪枝程度越小，也就是对原有的树只剪了那么一丢丢，不影响它的泛华能力。剪的越厉害，泛华能力相对会弱一些。
算法解释：第一轮对于决策树T₀选择剪枝系数最小的内部结点，减去这个内部节点的所有子树，只保留它本身得到决策树T₁。接着对于决策树T1执行相同的步骤得到T₂，就这样一直剪枝得到决策树T_K。
在这里插入图片描述
4、缺点与优点
时间开销大，但是欠拟合风险小，泛化能力好。

原文链接：https://blog.csdn.net/watermelon12138/article/details/83960049