前言

这是一份关于感知机模型的介绍，感知机作为神经网络的基础，其重要程度是可想而知的。感知机相对于其他的机器学习算法，其实现的难度却不是很大。感知机算是一个最常规的判别模型，它是通过输入空间的特征将实例划分为正负两类样本。感知机又分为原始形式和对偶形式，本文主要详细叙述原始形式。

一、感知机模型

感知机，是一个专门解决线性可分问题的线性分类器。在逻辑回归那一篇文章中，我们是找到一条合适的直线，从而能够分离两类数据。这其中的思想与本文所学的感知机是相似的，只不过逻辑回归是一个概率模型，最终求解得到的是类别为1的概率是多少，然后将概率大于0.5的样本划分为类别1，将概率小于0.5的样本划分为类别2，其中我们还用到了Sigmoid函数。在感知机模型中，我们同样的也是找到一条直线，使得该直线能够完美的将样本点区别开来。不需要得到样本点的概率情况，所以称感知机为一个判别模型。
那么我们如何能根据一条直线能够把样本的类别判断出来呢？
下面就又要引入一个新的函数：阶跃函数。
阶跃函数的形式如下：
$$sng(x)=\{\begin{array}{ll}1& x\ge 0\\ 0& x<0\end{array}$$
阶跃函数的图像如下：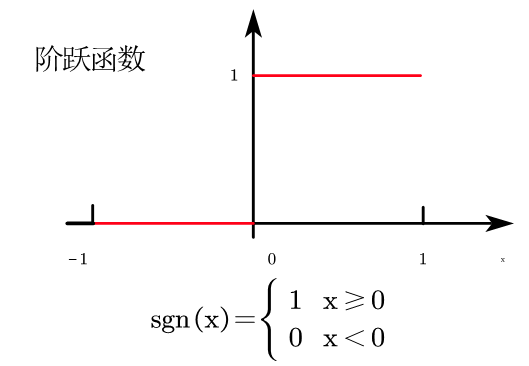

则才是阶跃函数的图像，我们要找到感知机的模型如下：

$$f(x)=sgn(w\cdot x+b)$$
$w$和$b$为感知机模型参数，$w$叫做权值，$b$叫做偏置，$w\cdot x$叫做内积。我们的任务就是通过给定的数据集找到合适的参数$w$和$b$，注意，感知机解决的问题一定是线性可分数据集，即对于线性不可分数据集简单的感知机是无法解决的。

二、感知机学习策略

既然已经知道感知机的模型是什么样子，那么我们该如何求出这个模型的表达式呢？在逻辑回归中，把极大似然函数作为损失函数来优化模型，那么在本文中该以什么函数作为损失函数呢？感知机的损失函数其实主要有两个思路，一是以误分类点的个数作为损失函数，但是误分类点的个数不是参数$w$和$b$的连续可导函数，不易优化。那么另一个策略就是以误分类点到超平面的总距离作为损失函数。

1.损失函数

假设感知机模型的超平面函数为$w\cdot x+b$，那么我们针对误分类的点$i$，该样本点$x_i$到超平面的距离可以表示为：
$$\frac{\left|w\cdot x+b\right|}{\Vert w\Vert }$$
其中$\Vert w\Vert$表示$w$的二范数。
对于误分类的点，假设该点真实属于1类，即$y_i=1$，但是通过感知机模型学习得到$w\cdot x_i+b<0$，于是对于分类错误的点来说：
$$y_i(w\cdot x_i+b)<0$$
这个表达式不管是针对真实$y_i=1$或者$y_i=-1$这两种情况都是适用的。
进一步得到：
$$-y_i(w\cdot x_i+b)>0$$
也是成立的。因此我们可以得到，误分类点$x_i$到超平面的距离为：
$$-\frac{1}{\Vert w\Vert }{y}_i(w\cdot x_i+b)$$
由于每次迭代过程中分类错误的点不止一个，我们设分类错误的点集合为$M$，则得到所有分类错误的点到超平面的总距离为：
$$-\frac{1}{\Vert w\Vert }\sum _{x_i\in M}{y}_i(w\cdot x_i+b)$$
不考虑$\frac{1}{\Vert w\Vert }$，就能得到感知机学习的损失函数。
可以明显看出，这个损失函数的值应该是非负的，我们可以认为当该损失函数最小时，对应的参数$w$和$b$就是最优的。

梯度下降法优化参数

在上一节中我们推导出感知机的损失函数，这一节需要对感知机的损失函数进行优化，数学模型如下：

$$\underset{w,b}{\min }L(w,b)=-\sum _{x_i\in M}{y}_i(w\cdot x_i+b)$$

其中$M$为误分类点的集合。
感知机学习算法是通过误分类驱动的，即如果所有点都被分类正确，学习停止。实现过程采用的是随机梯度下降法。首先任意初始化参数$w_0$和$b_0$，然后用梯度下降法不断地极小化目标函数，由于是随机梯度下降法，所以在梯度下降是只需要选取一个误分类点进行梯度下降。在实现过程中可以借助while循环，每次while循环下使用for循环遍历所有样本点，当有样本点出现误分类时，直接就使用这个误分类的样本点进行梯度下降，然后跳出for循环，如果for循环遍历所有样本点均未出现误分类点，则跳出while循环，学习结束。
既然想使用梯度下降法来优化参数，那么必须计算出损失函数$L(w,b)$的梯度：
$${\nabla }_{w}L(w,b)=-\sum _{x_i\in M}{y}_i{x}_i$$

$${\nabla }_{b}L(w,b)=-\sum _{x_i\in M}{y}_i$$
如果随机选择一个误分类样本点$(x_i,y_i)$，对$w,b$进行更新：
$$w\leftarrow w+\eta y_i{x}_i$$
$$b\leftarrow b+\eta y_i$$
式子中的$\eta$是步长，又称为学习率（梯度下降法中介绍过），于是我们就可以不断迭代损失函数$L(w,b)$，直到所有的样本点都被分类正确，此时的损失函数值应该为0。

三、算法实例

由于感知机模型求解的都是线性可分问题，于是我们仍采用Matlab实现感知机算法。
代码如下：

%% 感知机
clc,clear
tic
% 随机初始化数据
random = unifrnd(1,5,40,2);
X = [random(1:20,:);random(21:40,:)+5];
scatter(X(1:20,1),X(1:20,2),'o','filled')
hold on
scatter(X(21:40,1),X(21:40,2),'o','filled')
y = [zeros(20,1)-1;ones(20,1)]; % y标签
learn_rate = 0.01; % 定义学习率
% 感知机进行线性分类
w = [0,0];b = 0; % 初始化参数
while flag ~= length(X)
    flag = 0;
    for i =1:length(X) % 遍历所有样本点
        if y(i)*(w*X(i,:)'+b) <= 0 % 如果样本点存在分类错误的
            w = w + learn_rate * y(i) * X(i,:); % 更新参数
            b = b + learn_rate * y(i);  % 更新参数
            break; % 跳出循环
        else
            flag = flag + 1;
        end
    end
end
% 结果可视化
k = -w(1)/w(2); % 求斜率
b = -b/w(2); % 求系数
n = 1:1:10;
m = k*n+b;
hold on
plot(n,m,'--')
toc

结果如下：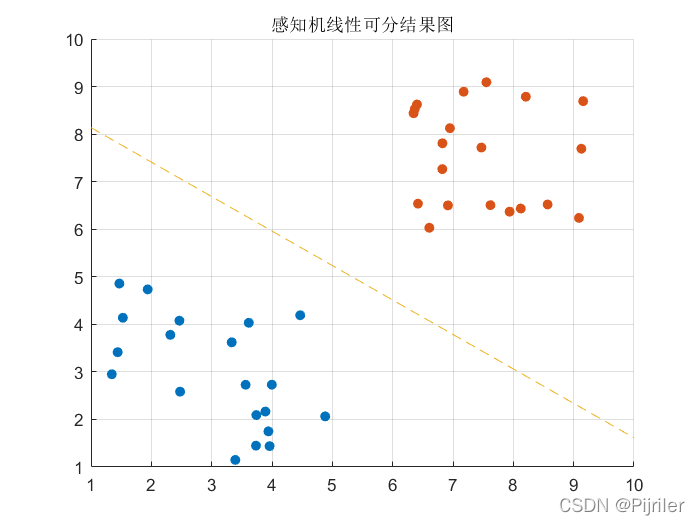

可以发现，感知机的最终结果其实就是一条直线，这条直线可以完全将两类线性可分数据进行分类，并且如果初始值选取不同时，感知机的学习结果也是不一样的，可以有很多条直线。

总结

感知机模型简单易懂，但是模型在解决线性不可分数据时便显得弱了些，如果想解决线性不可分数据的分类问题，可以采用支持向量机SVM来求解。