推荐算法_01_余弦相似度及TF-IDF算法

目录

1.1 余弦相似度介绍

1.2 余弦相似度举例

1.3 TF-IDF算法

1.1 余弦相似度介绍

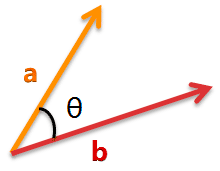
如何衡量两个向量的相似程度？我们用夹角的大小，来衡量向量的相似程度，夹角越小，向量越相似。

• 夹角0度：方向相同，线段重合，表示完全相似
• 夹角90度：方向正交，完全不相似

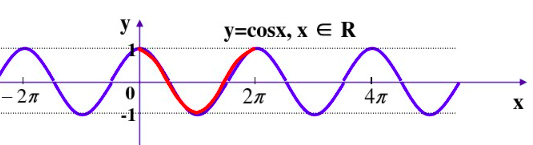
余弦曲线图：

以二维空间为例，向量a和向量b的余弦计算如下：

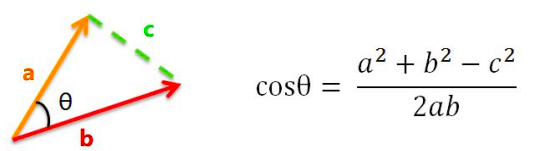
通常，向量是用坐标表示，向量a = [x1, y1]，向量b = [x2, y2]，那么余弦的计算形式如下：

推广到n维向量，假定向量A和向量B是两个n维向量，记A=[]，B=[]，那么余弦计算如下：

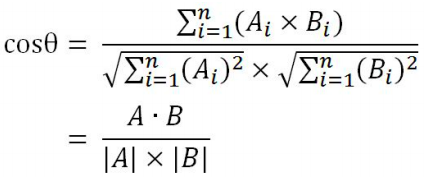
1.2 余弦相似度举例

简单起见，举个判断两个句子的相似度：

句子A：我喜欢看电影，不喜欢看电视剧

句子B：我不喜欢看电影，也不喜欢看电视剧

第一步：分词

句子A：我/喜欢/看/电影，不/喜欢/看/电视剧

句子B：我/不/喜欢/看/电影，也/不/喜欢/看/电视剧

第二步：列出所有词

[我，喜欢，看，电影，电视剧，不，也]

第三步：计算词频

句子A--->[我:1，喜欢:2，看:2，电影:1，电视剧:1，不:1，也:0]

句子B--->[我:1，喜欢:2，看:2，电影:1，电视剧:1，不:2，也:1]

第四步：向量表示

向量A--->[1, 2, 2, 1, 1, 1, 0]

向量B--->[1, 2, 2, 1, 1, 2, 1]

第五步：计算余弦相似度

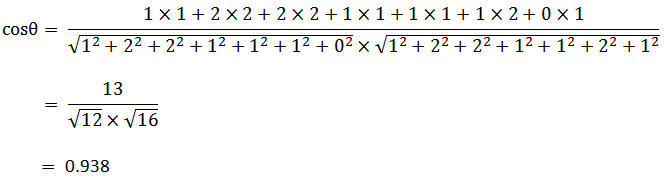
1.3 TF-IDF算法

参考：TF-IDF与余弦相似性的应用

参考：通俗易懂理解——TF-IDF与TextRank

参考：TF-IDF与余弦相似性的应用