第三次小班讨论课——海明检验码、用晶体管而不是逻辑门实现异或门

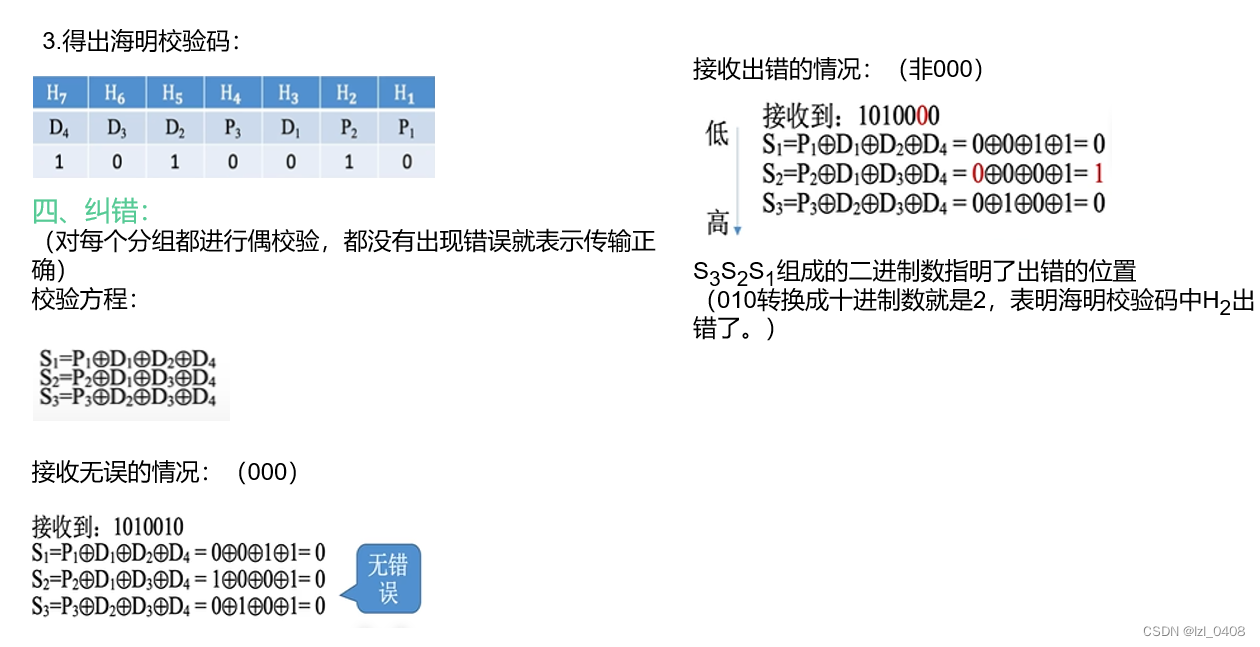
1. 上网查找海明检验码（又称汉明校验码）的编码原理，举例说明它是如何发现错误和纠正错误的。

海明码的编码原理

海明码——一种很有效的校验方法，是只要增加少数几个校验位，就能检测出二位同时出错、亦能检测出一位出错并能自动恢复该出错位的正确值的有效手段（自动纠错）。它的实现原理，是在n个数据位之外加上k个校验位，从而形成一个k+n位的新的码字。把数据的每一个二进制位分配在几个不同的偶校验位的组合中，当某一位出错后，就会引起相关的几个校验位的值发生变化。

海明码公式：2k-1≥ k +n

这个式子的意思是：假设为n个数据位设置k个校验位，则校验位能表示2k个状态，用来校验错误的数字个数（2k -1）要大于等于数据位数（n）和校验位数（k）的和。显然在2k中我们要留出一个数表示数据正确，所以我们用2k-1来代表出错的位数。

海明校验码设计思路：
1.将信息位分k(k为正整数)组进行偶校验，那么就得出k个校验位
2.且每个校验位都标注着是否出错和出错的位置

那么问题来了，应该分成几组呢？
1.假设信息位有n位，校验位有k位，
2.那么k个校验位就可以表示2^k种状态，
3.信息位+校验位共n+k位，且每一位都可能会出错，这就说明出错的状态会有n+k种，所以就能得出2^k >= n + k，
4.但是还有一种传输正确时的状态，所以最终为：2^k >= (n + k) + 1，
5.代入式子，就能求出校验位k的值，k为多少就表示分成几组。

海明校验码求解步骤：

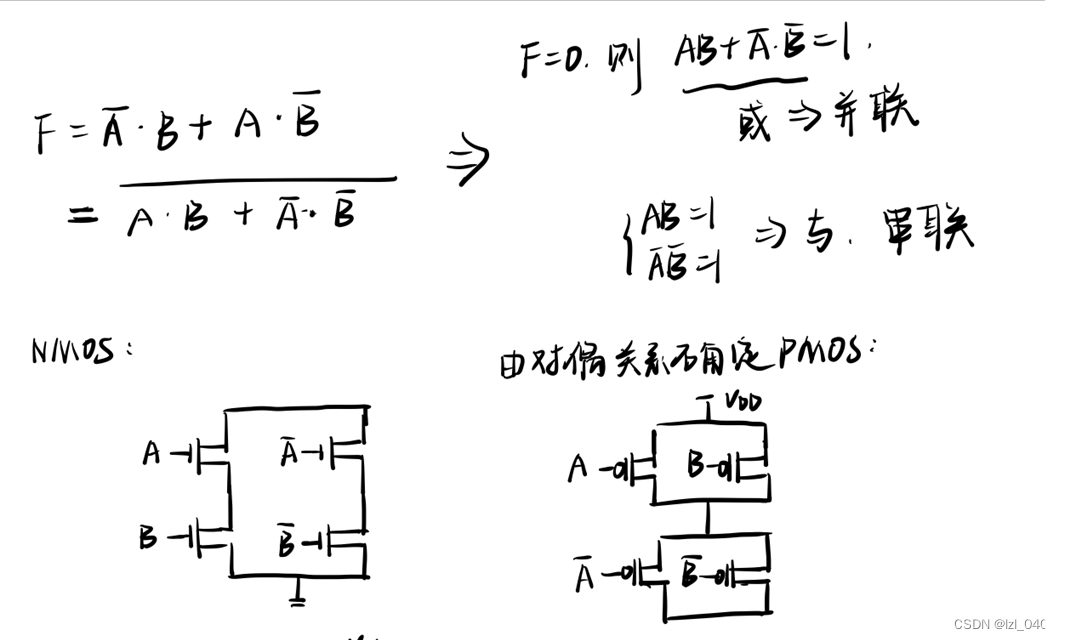
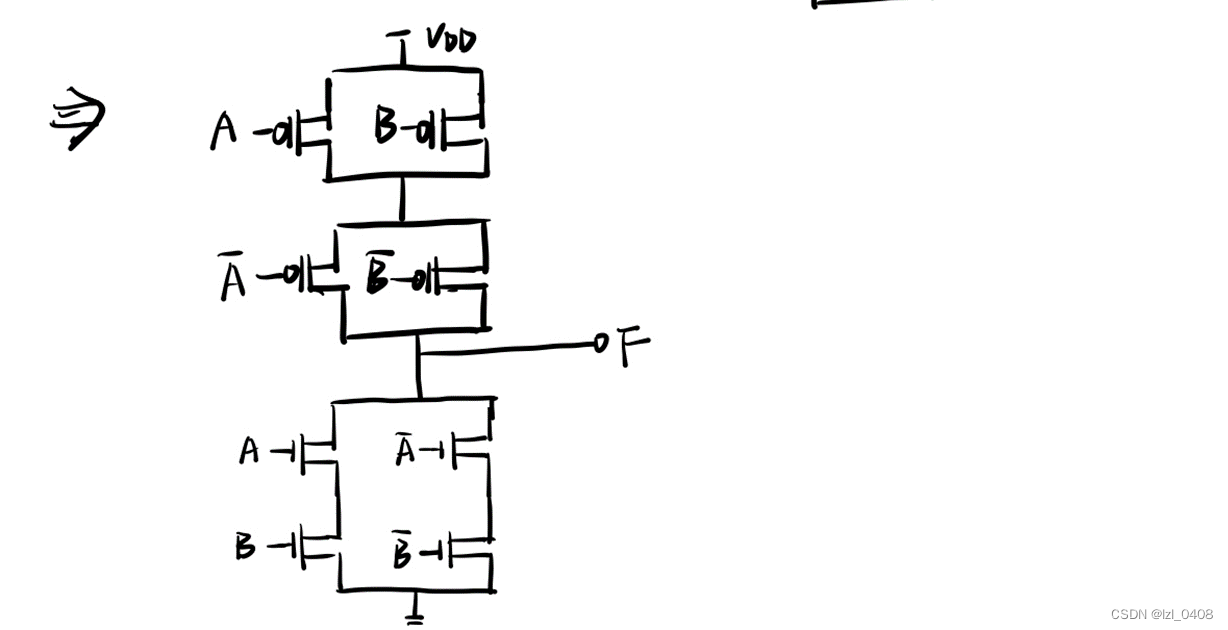
2. 直接用晶体管而不是逻辑门实现异或门，并解释这个电路是如何工作的。