统计相关性
算法
统计学一个最基本的关注点就是两个随机变量之间有没有相关性,或者说是否完全独立。所有学过统计学的人都知道最基本的Pearson相关系数。一般的统计学教授还知道统计书里的Spearman和Kendall这两种非参数方法。这三大方法的文章和讨论比比皆是,网上随便都能搜到。
注:非参数方法是指不对变量的总体概率分布做任何假设的统计方法
除了常见的三大方法外,还有许多不太知名的方法其实更加强大。想要全面的了解,笔者推荐这篇论文:“A comparative study of statistical methods used to identify dependencies between gene expression signals” (2014) 。这篇还不算太老的文章全面地总结了所有当时已知的相关性算法,并且用系统化的方法benchmark了它们的性能,是快速了解这一领域全貌的绝佳地图。本文中大部分图片都来自此篇paper,侵删。
相关性的几种分类方式
线性 v.s. 非线性
一般提到相关性,我们脑海中往往想的是线性相关性。如下图所示: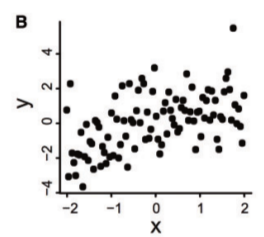
这幅图虽然不太明显,但大致还是能看出来x和y两个变量之间存在正线性相关关系,不难画出一条过0点斜率大概为1的直线来近似这种关系。Pearson相关性计算的就是线性相关程度,如果相关度高就可以进一步用Linear Regression来建模拟合线性模型了。
既然有线性相关,自然就有非线性相关。如下图所示: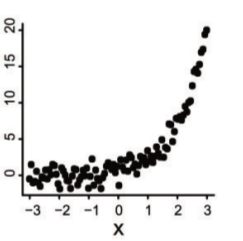
图中的点明显地指出了一个形如 y = e x − 1 y=e^x-1y=ex−1 的指数函数,你可以点击这里看看wolfram alpha画出来的此函数图形, 是不是拟合的很好?
像这种非线性相关关系,用Pearson方法就很吃力了。但还可以用spearman或者kendall来处理,因为这二者不使用变量的具体数值来计算,而是用值的相对大小(序数, rank)计算的。序数和比赛里的第一名,第二名一样,就是对一些数字(选手成绩)排序后的名次。比如对一个变量X={2,5,7,3}, 从小到大排序后的序数就是Rank(X)={1,3,4,2}。只要是一个值比另一个大,这两种算法就不在乎具体是线性还是非线性相关,都能正确地找出相关性。
单调(monotonic) v.s. 非单调(non-monotonic)
单调函数是指随着x的逐渐增大,y也会一直增大(或减小)的函数。反应在图上就是条一直上升(或下降)的线,不会中间突然改变上升或下降的趋势。上面的指数函数图就是一个单调函数。
违反单调函数定义的函数就是非单调函数了,图形上显示为一条随着x的增大, y时而上升而又时而下降的函数,如下图所示:
我们可以用一个形如 y = x 2 y=x^2y=x2 的多项式来拟合,看看wolfram画的图。
此图显示的是一个非线性,非单调的相关关系。这时就连spearman和kendall方法都失效了,因为这图上左半部分和右半部分的排序在计算过程中相互抵消,这两种方法会认为总相关性为0,从而错误地把x和y处理为独立关系。毕竟算法没长眼睛,不会看图。
注:这是机器学习和图像处理发挥特长的好机会
函数(Functional) v.s. 非函数(Non-functional)
这里数学没学好的同学(比如笔者)就要掉坑里了,因为一个基础概念很容易混淆:什么是函数?我们很容易认为函数和方程是一回事,就是包含变量的数学等式,但实际上二者是有区别的。
函数是指对于每一个自变量X的取值X0,都有因变量y的1个唯一取值Y0与之对应的方程。
用图形的方法解释,就是在函数图形上任意地点画一条垂直于x轴的直线,如果此直线与函数图形只有不超过1个交点,则为函数。举个反例: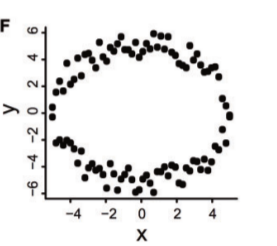
可以用形如 x 2 + y 2 = 5 x^2+y^2=5x2+y2=5 的圆形方程来近似拟合上图。
取x=0时,可以看到y有2个值: 大概是-6和6。这就违反了函数的定义,所以圆形方程只是方程,而不是函数。
上图这样的圆形(或椭圆)数据是最难找的相关关系之一,尤其在样本数很小(n<30)的时候,可以说是相关性算法的地狱,绝大多数算法都会被斩落马下,无法找到相关性。唯一的一个例外就是本文的主角HHG(Heller-Heller-Gorfine)算法。
整体相关(Global Correlation) v.s. 局部相关(Local Correlation)
如果两个随机变量X和Y的长度很长(样本数很多), 那么很有可能二者只在局部存在相关性。比如在某国的股票价格趋势中,X为某一只股票的价格,Y为此公司的年报中的业绩数据,那么很显然价格只会在年报刚发布后的一段时间内受到影响,二者只在短时间内出现了相关性。如果给定的是10年内累积的数据,那么从整体看二者就几乎体现不出任何相关性了。一部分算法可以找出局部相关性,包括我们的主角HHG。
总分类
把以上几种分类方法揉和起来,就形成了如下的总分类方法:
- 线性
- 非线性
- 函数
- 单调函数
- 非单调函数
- 非函数
- 函数
其中,每种分类还可以具体分成小样本(n<30)情况和大样本(n>=30)情况, 以及局部相关和整体相关的情况。所以一共3个维度能产生422=16种分类。比如一下两个极端的例子:
- 小样本,非线性非单调函数,局部相关
- 大样本,线性函数,整体相关
HHG
以色列特拉维夫大学的Ruth Heller, Yair Heller 两位统计学教授(犹太人也任人唯亲啊)和以色列技术学院的Malka Gorfine一起发明了这个算法,于2013年发表在Biometrika杂志上,并收录于arxiv。点这里看paper原文。这里对这三位学者表达一下敬意,在战火纷飞的中东还能做出如此杰出的学术贡献,祝三位平安。
相对于历史悠久的“老三样”算法,HHG算是小鲜肉了。但是不要被她粉嫩的外表欺骗了,这可以是目前为止唯一一个可以找到以上所有类别相关关系的算法之王。下面我们来具体了解一下她。
对于随机变量X和Y,即使X和Y都是多维向量(矩阵),强大的HHG也是可以计算的。这里为了简化阐述,默认X和Y都是一维向量,也就是一个表格中的两列(或者两行)。
HHG借鉴了spearman和kendall等算法里的排序思想,以及卡方独立性检验(Chisquare Test for Independence)的方法。必须先理解卡方检验以及其使用的列联表(Contingency Table)的概念,可以参见这篇很好的博文, 这里就不重造轮子了。
下面我们先来机械地介绍HHG算法的计算过程,然后再来尝试理解她背后的含义。
为了方便说明,这里拿一个小dataset举例,为方便计算全部取整数:
| 行号(i) | X | Y |
|---|---|---|
| 1 | 1 | 12 |
| 2 | 2 | 20 |
| 3 | 3 | 30 |
| 4 | 4 | 9 |
| 5 | 5 | 10 |
算法步骤
遍历每一行,即从表格的第1行开始,逐个计算直到最后一行,计算的过程是这样的:
- 设i为遍历用的行号,i=1, X(i)=1,Y(i)=12
- 固定i=1,遍历所有其他行,设j为遍历用的行号(j ! = i j!=ij!=i)。
- j=2, X(j)=2,Y(j)=20
- 设 函数d(a, b)=|a-b|, 也就是说这个d()函数计算两个输入值之差的绝对值。如果a和b推广为向量,则这里计算的就是两个向量之间的距离。HHG算法不定义具体使用哪种距离,只要求用户提供计算好的距离。对于标量,我们可以也可以选用平方差。对于向量,则有多种选择,常见的如闵可夫斯基距离,余弦相似度,KL散度等等。各种距离度量各有其优缺点,具体可以参考这篇总结的很全面的博文。
- 计算d(xi, xj) = |x1-x2| = |1-2|=1,将其设为一个新的变量Rx, Rx=1
- 类似地,计算d(yi, yj) = |y1-y2| = |12-20|=8,将其设为一个新的变量Ry, Ry=8
- 固定j,遍历所有其他行。设k为遍历用的行号(k!=i AND k!=j)。k=3, X(k)=3, Y(k)=30
- 计算d(xi, xk) = |x1-x3| = |1-3|=2
- 类似地,计算d(yi, yk) = |y1-y3| = |12-30|=18
- 设变量A11=0,A12=0,A21=0,A22=0,这些都是下面要用到的累计计数。
- 比较d(xi, xk)和Rx的值, 类似地,比较d(yi, yk)和Ry的值,比较结果共有4种情况(见表2):
如果d(xi, xk)<=Rx 而且d(yi, yk)<=Ry, 则A11加1。其他情况可以按照表格理解。A1.=A11+A12, 其它类似的行/列之和参见表格。N表示总行数(样本数)。 - k加1,重复步骤7到11, 累加A*系列变量,此时表格如表3所示
- 此时有了i=1,j=2情况时的列联表,就可以使用卡方检验来计算了。公式如下:
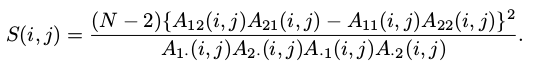
- 对于当前i=1, j=2的情况, 计算可得S(i,j)=0
- j加1, j=3, X(j)=3, Y(j)=30。
- 重复步骤5到16, 在每一步都计算S(i,j)并累加起来。计算后得出i=1时的总S(i,j)= 3 (计算省略)
- i加1, i=2, X(i)=2.
- 重复步骤3到18, 直到穷尽所有的i (行) 为止。把所有的S(i,j)累加起来,得到最终的S(i,j) = 5.25。这个值代表了在当前自由度下两个变量的相关强度。值越大则强度越大。
- 进行置换检验 (Permutation Test)。置换检验的概念可以参考这篇好文。这里具体的方式是,保持X的值排序不变,以随机的方式重新排列Y变量的值,也就是打乱Y变量值的行号。重复999次,每次都计算S(i,j)的值,加上第一次算出的S(i,j)一共1000个值形成一个分布。如果两变量是非独立的,那么原始数据集的Y排列方式应该很少见,也就是S(i,j)>=5.25的值应该在此分布中很少出现。相反,如果两变量独立,则原始排列应该没有任何特殊之处,即>=5.25的值应该很常见。如果有n个>=5.25的值,那么最终的p值就是n/1000。这个p值越小,则两个变量相关的可能性就越大。由于是随机排列,每次计算的p值有一个上下浮动。大概为0.9。
- 根据p值决定是否推翻原假设(两变量独立不相关)。如果以0.05为阈值,则0.9>>0.05, 无法推翻原假设,说明两个变量独立。
表2
| d(yi, yk)<=Ry | d(yi, yk)>Ry | ||
|---|---|---|---|
| d(xi, xk)<=Rx | A11 | A12 | A1. |
| d(xi, xk)>Rx | A21 | A22 | A2. |
| A.1 | A.2 | N-2 |
表3: i=1, j=2时的列联表
| d(yi, yk)<=Ry | d(yi, yk)>Ry | ||
|---|---|---|---|
| d(xi, xk)<=Rx | 0 | 0 | 0 |
| d(xi, xk)>Rx | 2 | 1 | 3 |
| 2 | 1 | 3 |
R语言实现
hhg_cal()计算给定数据的S(i,j)统计量。
> hhg_cal<-function(df){
n=nrow(df)
a<-1:n
s=0
for (i in a){
for(j in a[a!=i]){
rx <- abs(df[i,1]-df[j,1])
ry <- abs(df[i,2]-df[j,2])
a11 = a12 = a21 = a22 = 0
for(k in a[a!=i & a!=j]){
if (abs(df[i,1]-df[k,1]) <= rx){
if(abs(df[i,2]-df[k,2]) <= ry){
a11 = a11+1
}else{
a12 = a12+1
}
}else{
if(abs(df[i,2]-df[k,2]) <= ry){
a21 = a21+1
}else{
a22 = a22+1
}
}
}
a1_=a11+a12
a2_=a21+a22
a_1=a11+a21
a_2=a12+a22
if (a1_*a2_*a_1*a_2 ==0){
s_new = 0
}else{
s_new = (n-2)*(a12*a21-a11*a22)^2/(a1_*a2_*a_1*a_2)
}
s = s+s_new
}
}
#print(s)
return(s)
}
hhg_perm_test()对Y随机置换,然后调用hhg_cal()计算新的S值。
> hhg_perm_test<-function(s_target){
x<-c(1,2,3,4,5)
y<-c(12,20,30,9,10)
Y<-sample(Y)
X<-matrix(c(x,Y),ncol=2)
s<-hhg_cal(X)
return(s)
}
创建数据集,计算s_target(第一次计算得到的S值),然后调用hhg_perm_test()进行置换检验。对结果画图,计算p值并显示。
> X<-matrix(c(1,2,3,4,5,12,20,30,9,10),ncol=2)
> s_target<-hhg_cal(X)
> results<-replicate(999,hhg_example(s_target))
> hist(results,breaks=20,prob=TRUE)
> lines(density(results))
> p.value<-length(results[results>=s_target])/1000
> p.value
>[1] 0.9003

上图中x轴代表每次随机检验得到的S值,y轴代表其概率密度。可以看到对原始数据计算得到的S=5.25非常靠左,>=5.25的情况非常常见,换言之原始数据的排列方式相对随机排列没有什么特殊之处,所以两个变量基本没有相关性。
时间复杂度
从R代码可以看出,这个算法是一个对i, j, k 的3层嵌套循环,所以时间复杂度是O(n 3 n^3n3),n为变量的长度(数据集的行数),比较慢,对大数据不够友好。论文中给出了一种优化的方案可以精简到O(n 2 n^2n2log(n))。
R Package
论文的作者们用R语言实现了HHG算法并贡献到了CRAN,可以在这里找到。这个包质量很高,不但提供了一个example data generator函数,而且还良心地加入了多线程支持,在R包里可不多见。我们用作者写的HHG包来实现一下本文中的示例。
直接从cran安装包:
> install.packages("HHG")
创建数据,HHG接受2行多列的Matrix作为输入,每一行代表一个变量。
> X<-matrix(c(1,2,3,4,5,12,20,30,9,10),nrow=2, byrow=T)
画个图看看
> plot(X[1,],X[2,])

前面提到,HGG不定义距离的计算,由用户提供。hgg.test()函数分别接受X和Y变量取值间的距离作为输入,也就是第5和第6步中计算的Rx和Ry的值。这里我们需要先把所有的Rx和Ry计算来,以矩阵的形式传入hgg.test()。
> Dx = as.matrix(dist((X[1,]), diag = TRUE, upper = TRUE))
> Dy = as.matrix(dist((X[2,]), diag = TRUE, upper = TRUE))
使用hhg算法计算相关性并打印结果:
> set.seed(1) #这里是为了多次运行时产生相同的伪随机数,以至于产生相同的p值。
> hhg = hhg.test(Dx, Dy, nr.perm = 1000) #进行1000次置换检验。
> hhg
Results for the HHG test of independence:
Number of observations: 5
Sum of chi-squared scores of all 2X2 tables: 5.250
P-value for the sum of chi-squared scores statistic : 0.902
Sum of likelihood ratio scores of all 2X2 tables: 3.479287
P-value for the sum of likelihood ratio scores statistic : 0.893
Maximum over chi-squared scores of all 2X2 tables: 0.000
P-value for the max of chi-squared scores statistic : 1
Maximum over likelihood ratio scores of all 2X2 tables: 1.909543
P-value for the max of likelihood ratio scores statistic : 0.9
R包的计算结果(使用chi-square时)是0.902,与我们自己实现的R代码的结果0.9003差不多,差异是由随机数造成的。
我们再来用HHG包做一个有相关性的例子,使用如下数据集:
| 行号(i) | X | Y |
|---|---|---|
| 1 | 1 | 10 |
| 2 | 2 | 20 |
| 3 | 3 | 30 |
| 4 | 4 | 40 |
| 5 | 5 | 50 |
输出结果是:
Results for the HHG test of independence:
Number of observations: 5
Sum of chi-squared scores of all 2X2 tables: 36.000
P-value for the sum of chi-squared scores statistic : 0.0163
Sum of likelihood ratio scores of all 2X2 tables: 22.91451
P-value for the sum of likelihood ratio scores statistic : 0.0163
Maximum over chi-squared scores of all 2X2 tables: 0.000
P-value for the max of chi-squared scores statistic : 1
Maximum over likelihood ratio scores of all 2X2 tables: 1.909543
P-value for the max of likelihood ratio scores statistic : 0.806
p值为0.0163 < 0.05,可以认为两个变量存在相关性。
算法思想
HHG基本是对Kendall和卡方检验的融合与推广。她先计算Kendall中变量值的排序(大小关系)(而且利用距离的概念推广到了向量),再对排序(大小关系)使用卡方检验,最后用置换验证得出p值。
给定2个随机变量X和Y,X的概率分布为Px,Y的概率分布为Py,则X与Y有一个联合概率分布Pxy。 现在说人话,小明军训去靶场射击,一共开了5枪,都上靶了。怎么用数学方法表示这5枪的位置呢?
我们以靶心为原点建立一个平面直角坐标系,再测量这个弹孔的坐标位置,如下图所示:
5个弹孔坐标的x轴分量可以视为随机变量X, X={-2,-1,0,0.5,1},相应地其y轴分量可以视为随机变量Y, Y={1,-1,0,-0.3,1}。单独审视这两个变量时,它们各有自己的概率分布:
x概率分布
y概率分布
上面2个直方图中,x轴为随机变量的取值,y轴为x=某个值时的概率。图中的曲线代表概率密度,其含义是x处于某个值区间(比如[-0.5, 0])的概率等于在此区间上概率密度曲线下的面积(就是对曲线的积分)。曲线下的总面积=1 (因为总概率为1)。
把X和Y统一起来考虑,组合成一个新的二维随机变量Z。X,Y的取值以及Z的概率可以张开一个三维直角坐标系,在其中显示联合概率分布,如下图所示:
上图中,X分量和Y分量的概率密度函数称为边缘概率分布(Marginal Probability Distribution),记为Fx, Fy。Z的概率密度函数称为联合概率分布(Joint Probability Distribution),记为Fxy。原假设H0是X和Y完全独立,此时,Fxy = Fx*Fy;如果二者不独立(存在相关关系),则Fxy != Fx*Fy,可以推翻原假设。本算法的中心思想就是计算Fxy(实际概率分布) 和 Fx*Fy (原假设下的理论概率分布)并判断是否相等。
从图形上说,就是上图中选择一点(x0, y0), 选定一个X轴的半径Rx和一个y轴的半径Ry, 可以形成1个椭球B(实在太难画了,回头补图), B以(x0, y0)为中心,x轴方向上半径为Rx, y轴方向上半径为Ry。B里面所有的点的集合Sxy代表B里所有可能出现的(x,y)的值。Sxy里每一个(x,y)的值都对应着一个概率值,所有的概率值的集合就是实际概率密度函数Fxy。
因为我们没法很好的选择(x0, y0)的值,也不知道Rx和Ry应该取什么值,就干脆使用样本数据来定义。先选择Z的第一个样本s1做为(x0, y0),再计算s1与s2的距离来作为Rx/Ry, 就可以生成椭球B了,然后遍历其他的样本点,看看它们落在椭球内的概率是多少,就可以算出实际的概率密度,再与理论概率密度做差,这个差就是S(i,j)的值。这个值越大说明实际概率和理论概率相差越大,越可能推翻H0。
然后重新选择s1与s3的距离来作为Rx/Ry,重新生成椭球球再计算,重复这个过程直到所有距离都被使用过。再选择下一个样本点s2作为新的球心,重复整个过程并累加S(i,j)的值。
局部相关性
免责声明:此部分内容不属于原论文,是笔者自己加上的,可能存在错误,笔者不对使用者负任何责任。
HHG可以找出局部相关性,但不直接告诉我们是哪些样本的集合存在相关性,所以我们自己还要多做一些工作来找出这些样本点的行号。
因为HHG遍历所有的样本点和距离来计算S(i,j), 并且记录了所有i和j情况下的S(i,j),所以我们可以从这方面来入手。因为2x2列联表的自由度是固定的1, 所以我们可以提前查询卡方分布表来p<=5%对应的卡方值S(i,j)>=3.841。
一个S(i,j)>=3.841的椭球B(i,j) 内部包含的样本点在都可能相关,这些B(i,j)的集合{B(i,j)} 还要经过置信检验才可以确定。鉴于在大数据中这种计算负担太大,我们可以进行一点优化,即对于每个固定的i值I, 只在{B(I,j)}中选择包含样本数最多的椭球{Bmax(I)} (可能有多个),并记录每一个椭球中包含的样本行号。遍历所有的i后,我们得到所有的候选椭球集合{Bmax}。然后使用之前记录的样本行号,对集合中的每一个椭球进行置信检验,进一步选出p值<5%的椭球。这些N个最终赢家椭球就代表了N中局部相关的情况。
看起来这些工作增加了计算负担,但从大数据处理的角度看,能够直接找出局部相关性能够避免暴力穷解,总体上其实节省了很多时间。